Тема 2.11. Усовершенствованный симплекс-метод

Обычный симплекс-метод предполагает использование обычных симплекс-таблиц. В усовершенствованном симплекс-методе применяются другие таблицы, которые, в частности, не содержат столбцов, соответствующих базисным переменным.

Мы видели в рассмотренных ранее примерах, что только один из них изменяется, это и навело на мысль не писать их в таблице совсем. Принцип выбора разрешающего элемента сохраняется. При переходе к очередной симплекс-таблице также используется «правило прямоугольника». Особенность состоит лишь в преобразовании элементов разрешающей строки и разрешающего столбца: разрешающий элемент надо заменить ему обратным, все другие элементы разрешающей строки и разрешающего столбца надо разделить на разрешающий элемент, сменив при этом знаки у элементов столбца на противоположные.

Пример. Найти наибольшее значение функции f = 2 x ₁+ 3 x ₂, если переменные х ₁, х ₂ неотрицательные и удовлетворяют системе ограничений:

Решение. Вводим балансовые переменные х ₃, х ₄, х ₅ и превращаем систему неравенств в систему уравнений. Принимаем балансовые переменные в качестве базисных переменных, а х ₂, х ₁ – в качестве свободных переменных и составляем первую симплекс-таблицу.

Таблица 2.15

Б.п.	х 1	х 2	с.к.
х 3
х 4	-2	3
х 5		-1
f	-2	-3

Так как g ₂ = -3 – наибольший по модулю отрицательный индекс, то второй столбец является разрешающим. Так как min, то вторая строка является разрешающей. Таким образом, а ₂₂ = 3 – разрешающий элемент. Разрешающий элемент 3 заменяем ему обратным, т.е. на Элементы второго столбца и второй строки (кроме разрешающего) делим на 3, при этом у элементов столбца меняем знаки на противоположные. Остальные элементы таблицы 2.15 преобразуем по «правилу прямоугольника». Переменные х ₂, х ₄ меняем местами. Получаем таблицу 2.16.

Таблица 2.16

Б.п	х 1	х 4	с.к
х 3		-1
х 2	-2/3	1/3
х 5	7/3	1/3
f	-4

Выбрав а ₁₁= 7 в качестве разрешающего элемента, поменяв переменные х ₁, х ₃ местами, преобразовав элементы таблицы 2.16 указанным выше образом, приходим к таблице 2.17.

Таблица 2.17

Б.п.	x 3	х 4	с.к.
х 1		-	9/7
х 2	2/21	5/21	20/7
х 5	-1/3	2/3
f	4/7	3/7	78/7

Так как в нижней строке таблицы 2.17 нет отрицательных индексов, то f_max =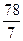и – оптимальный план.

Тема 2.12. метод искусственного базиса (М-метод)

Важным в применении симплекс-метода является отыскание первого базисного решения. Мы рассматривали примеры, в которых этот вопрос решался очень просто путем введения балансовых переменных. Но не в каждом примере так можно поступить. Поэтому применяются и другие методы отыскания базисных решений. Мы рассмотрим М-метод (метод искусственного базиса).

Пусть требуется найти наибольшее значение функции

f = c ₁ x ₁ + c ₂ x ₂ +...+ c_nx_n, если переменные х ₁, х ₂,..., х_n неотрицательные и удовлетворяют системе уравнений:

(*).

где b ₁³ 0, b ₂³ 0,..., b_m ³ 0.

Будем предполагать, что матрица коэффициентов при переменных величинах системы не содержит единичной матрицы размера m х m. В противном случае – переменные, соответствующие единичной матрице, принимаем в качестве базисных, а остальные – в качестве свободных переменных и получаем первое базисное решение, состоящее из нулей и свободных коэффициентов системы. Таким образом, наличие единичной матрицы размера m x m в матрице коэффициентов при неизвестных в системе уравнений позволяет быстро составить базисное решение.

Рассмотрим расширенную задачу. Найти наибольшее значение функции:

Z = c ₁ x ₁ + с ₂ х ₂ +...+ с_n x_n - M (x_{n +1} +...+ x_n+m),

где с ₁ х ₁ + с ₂ х ₂ +...+ с_n x_n = f,

М – достаточно большое произвольное положительное число, если переменные х ₁, х ₂,..., х_n, x_{n +1},..., x_{n + m} неотрицательные и удовлетворяют системе уравнений:

(**)

Для получения расширенной задачи надо в левую часть каждого уравнения системы (*) прибавить по одной из фиктивных переменных х_{n +1},..., x_{n + m ,}, а из целевой функции f вычесть сумму всех фиктивных переменных, умноженную на произвольное достаточно большое положительное число М. Переменным x_{n +1}, x_{n +2},..., x_{n + m} в системе (**) соответствует единичная матрица размера m х m и, следовательно, приняв их в качестве базисных переменных, легко можно найти базисное решение системы.

Теорема. Если 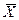(х ₁, х ₂,..., х_n, 0,..., 0) является оптимальным планом расширенной задачи, то Х (х ₁, х ₂,..., х_n) является оптимальным планом исходной задачи линейного программирования, при этом f_max = Z_{max .}

Доказательство. Очевидно, если 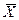удовлетворяет системе (**), то Х удовлетворяет системе (*), при этом

Z (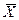) = f (X).

Пусть 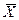– оптимальный план расширенной задачи, докажем, что Х – оптимальный план исходной задачи. Допустим, что Х не является оптимальным планом. Тогда существует такой оптимальный план Х ¢(х ¢₁, х ¢₂,..., х ¢ _n), что f (X)< f (X ¢). Для

получаем:

Таким образом, 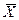не является оптимальным планом расширенной задачи, что противоречит условию теоремы. Теорема доказана.

Пример. Найти наибольшее значение функции f = 2 x ₁ - x ₄, если переменные х ₁, х ₂, х ₃, х ₄, х ₅, х ₆ неотрицательные и удовлетворяют системе уравнений:

Решение. Для получения единичной матрицы в системе ограничений достаточно к левой части второго уравнения прибавить фиктивную переменную х ₇. Расширенная задача будет иметь следующую формулировку. Найти наибольшее значение

функции Z = 2 x ₁ - x ₄- Mx ₇, если переменные х ₁, х ₂,..., х ₇ неотрицательные и удовлетворяют системе уравнений:

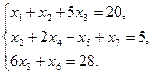
Выразим Z через свободные переменные х ₂, х ₃ , х ₄ , х ₅.

Z = 2(20- x ₂-5 x ₃)- x ₄ - M (5 - x ₂ - 2 x ₄ + x ₅) = (40 - 5 M) + (M - 2) x ₂ -10 x ₃++(2 M -1) x ₄- Mx ₅.

Составим первую симплекс-таблицу.

Таблица 2.18

Б.п.	х 2	х 3	х 4	х 5	c.к.
х 1
х 7			2	-1
х 6
Z	2- М		1-2 М	М	40 -5 М

Помня, что М – достаточно большое положительное число, заключаем, что (1- 2М) - наибольший по модулю отрицательный индекс нижней строки таблицы 2.18. Поэтому третий столбец является разрешающим. Ясно, что вторая строка является разрешающей. Таким образом, а ₂₃ = 2 – разрешающий элемент. Путем известных нам преобразований приходим к таблице 2.19.

Таблица 2.19

Б.п.	х 2	х 3	х 7	х 5	с.к.
х 1
х 4	1/2		1/2	-1/2	5/2
х 6
Z	3/2		М-1/2	1/2	37,5

Так как в последней строке таблицы 2.19 нет отрицательных индексов (М >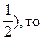 Z_max = 37,5 и (20, 0, 0, 0, 28, 0) – оптимальный план расширенной задачи. Значит f_max = 37,5 и

(20, 0, 0, 0, 28) – оптимальный план исходной задачи.

Дата добавления: 2014-10-31