
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделей нелинейного программирования
|
|
|
|
Тема 3.4. Примеры экономико-математических
Задача. Предприятие имеет возможность доставить свою продукцию в количестве 400 тонн потребителю двумя видами транспорта (железнодорожным и автомобильным). Транспортные расходы при перевозке х 1 тонн груза по железной дороге равны 100 х 1 денежных единиц, а транспортные расходы при перевозке х 2 тонн груза автомашинами равны  денежных единиц. Найти оптимальный план перевозки продукции при котором транспортные расходы были бы наименьшими.
денежных единиц. Найти оптимальный план перевозки продукции при котором транспортные расходы были бы наименьшими.
Решение. В данной задаче надо найти минимум функции  при условии, что х 1 + х 2 = 400. Для этого составляем функцию Лагранжа
при условии, что х 1 + х 2 = 400. Для этого составляем функцию Лагранжа

и находим ее частные производные.
 ;
;  ;
;  .
.
Решаем систему уравнений:

Получаем:
l =-100; х 2=50, х 1=350.
Следовательно,
f = f (350; 50) = 100×350 + 502 = 37500 –
наименьшие транспортные расходы, а (350; 50) – оптимальный план доставки продукции.
Задача. Для производства двух видов изделий А и В предприятие использует три типа технологического оборудования, причем каждое изделие проходит обработку на каждом из них. Время обработки одного изделия, денежные затраты, связанные с этим, ресурсы времени использования оборудования указаны в таблице.
Таблица 3.1
| Тип оборудования | Затраты времени на обработку одного изделия (час.) | Ресурсы времени (час.) | |
| А | В | ||
| I | £20 | ||
| II | ³5 | ||
| III | £30 | ||
| Затраты на производство одного изделия (тыс. руб) |
Определить сколько изделий каждого вида надо изготовить, чтобы средние затраты на производство одного изделия были наименьшими.
Решение. Пусть (х 1, х 2) – план производства изделий. Тогда 2 х 1+3 х 2 – общие затраты денежных средств на производство изделий А и В, а  – средние затраты на производство одного изделия. Для решения поставленной задачи надо найти наименьшее значение функции f при условии, что
– средние затраты на производство одного изделия. Для решения поставленной задачи надо найти наименьшее значение функции f при условии, что
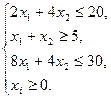
Строим область ограничений в системе координат х 1 ох 2. Она представляет собой треугольник АВС с уравнениями сторон: 2 х 1 + 4 х 2 = 20, х 1 + х 2 = 5, 8 х 1 + 4 х 2 = 30 (см. рис. 3.6.).
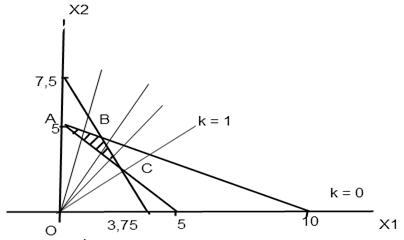
Рис.3.6. Геометрический метод
Выразим х 2 через х 1 и f. Получим:: fx 1+ fx 2 = 2 x 1+ 3 x 2, 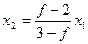 , x 2 = kx 1, где
, x 2 = kx 1, где  . Уравнение х 2 = kx 1 представляет собой при переменном значении k пучок прямых с центром в начале координат. Выразим f через k. Получим:
. Уравнение х 2 = kx 1 представляет собой при переменном значении k пучок прямых с центром в начале координат. Выразим f через k. Получим:  . Найдем производную от f по k. Получим:
. Найдем производную от f по k. Получим:
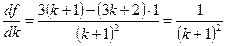 .
.
Так как  , то f возрастает при возрастании k. Следовательно, при вращении прямой х 2 = kx 1 против часовой стрелки целевая функция возрастает, поэтому f min = f (С). Находим координаты точки С, решая систему уравнений
, то f возрастает при возрастании k. Следовательно, при вращении прямой х 2 = kx 1 против часовой стрелки целевая функция возрастает, поэтому f min = f (С). Находим координаты точки С, решая систему уравнений

Получаем,  . Следовательно
. Следовательно  и
и  –
–
оптимальный план производства изделий.
Тема 3.5. Задача выпуклого программирования
Для формулировки задачи выпуклого программирования используются понятия выпуклого множества и выпуклой функции.
Напомним, что множество называется выпуклыми, если отрезок, соединяющий любые его точки, принадлежит этому множеству. Таким образом, если Х – выпуклое множество, а 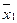 и
и  любые его две точки, то при любом t Î[0; 1] точка
любые его две точки, то при любом t Î[0; 1] точка 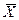 = (1- t)
= (1- t) + t
+ t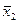 принадлежит множеству Х.
принадлежит множеству Х.
Если для любого t Î(0; 1) и любых двух точек  ,
, 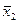 выпуклого множества Х выполняется соотношение:
выпуклого множества Х выполняется соотношение:
f ((1- t) + t
+ t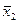 ) £ (1- t) f (
) £ (1- t) f ( ) + tf (
) + tf (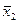 ),
),
то функция f ( ) называется выпуклой, а если выполняется соотношение:
) называется выпуклой, а если выполняется соотношение:
f ((1- t) + t
+ t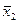 ) ³ (1- t) f (
) ³ (1- t) f ( ) + tf (
) + tf (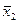 ),
),
то функция f ( ) называется вогнутой.
) называется вогнутой.
Для функции одного переменного выпуклость означает, что ее график лежит ниже хоры, соединяющей любые две его точки, а вогнутость означает, что ее график лежит выше хорды, соединяющей любые две его точки.
Задачу математического программирования в общем виде можно сформировать так: найти оптимальное (наибольшее или наименьшее) значение целевой функции f ( ) на множестве Х и точку
) на множестве Х и точку  , в которой оно достигается.
, в которой оно достигается.
Если в задаче математического программирования множество Х выпукло и функция f ( ) выпукла, то она называется задачей выпуклого программирования.
) выпукла, то она называется задачей выпуклого программирования.
Если  , причем все функции ji (
, причем все функции ji ( ) вогнутые, а целевая функция f (
) вогнутые, а целевая функция f ( ) выпуклая на Х, то задача минимизации f (
) выпуклая на Х, то задача минимизации f ( ) на Х называется основной задачей выпуклого программирования.
) на Х называется основной задачей выпуклого программирования.
Отметим, что вогнутость функций системы ограничений обеспечивает выпуклость области ограничений. Действительно, если 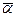 ,
,  Î Х, т.е. ji (
Î Х, т.е. ji (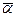 )³0 и ji (
)³0 и ji ( )³0 для
)³0 для  , то:
, то:  , так как 1- t ³0,
, так как 1- t ³0,  ³0,
³0,  ³0, t ³0.
³0, t ³0.
Для формулировки критерия оптимальности целевой функции, т.е. теоремы Куна-Таккера, нам понадобится понятие седловой точки функции.
Определение. Пара  ,
,  , называется седловой точкой функции F (
, называется седловой точкой функции F ( ,
, ) на множестве всех
) на множестве всех  , принадлежащих некоторому выпуклому множеству п -мерных векторов Х и
, принадлежащих некоторому выпуклому множеству п -мерных векторов Х и  , принадлежащих множеству т -мерных векторов с неотрицательными координатами
, принадлежащих множеству т -мерных векторов с неотрицательными координатами  , если
, если  ÎХ,
ÎХ,  Î
Î и F (
и F ( ,
,  )£ F (
)£ F ( ,
,  )£ F (
)£ F ( ,
,  ) для всех
) для всех  ÎХ и
ÎХ и  Î
Î .
.
Последнее неравенство можно записать в следующей форме: 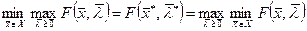 .
.
Теорема Куна–Таккера. Если в задаче выпуклого программирования
 ,
, ,
,
множество Х обладает свойствами регулярности, т.е. для каждого  существует такая точка
существует такая точка  , что
, что  , то необходимым и достаточным условием оптимальности точки
, то необходимым и достаточным условием оптимальности точки  Î Х является существование такого
Î Х является существование такого  ³0, чтобы пара
³0, чтобы пара  ,
,  являлась седловой точкой функции Лагранжа
являлась седловой точкой функции Лагранжа
F ( ,
,  ) = f (
) = f ( )-
)- на множестве
на множестве  ,
, 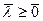 .
.
Теорема Куна-Таккера занимает важное место в теории выпуклого программирования. Она представляет собой обобщение классического метода множителей Лагранжа на случай, когда ограничения на переменные являются не только уравнениями, но и неравенствами.
Теперь сформулируем условие существования седловой точки.
Теорема. Для того, чтобы пара  ,
,  (
(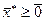 ,
,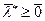 ) была седловой точкой непрерывно дифференцируемой функции
) была седловой точкой непрерывно дифференцируемой функции  , которая выпукла для всех
, которая выпукла для всех  Î
Î и вогнута по
и вогнута по  для всех
для всех  Î
Î , необходимо и достаточно чтобы при
, необходимо и достаточно чтобы при  =
= ,
,  =
= выполнялись условия:
выполнялись условия:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 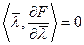 .
.
Пример. Найти наименьшее значение функции
f (x 1, x 2) =  , если x 1 ³ 0, х 2 ³ 0, х 1 + х 2 ³ 4.
, если x 1 ³ 0, х 2 ³ 0, х 1 + х 2 ³ 4.
Решение. Так как функция  выпуклая и ограничения задаются линейными, следовательно вогнутыми, функциями, то рассматриваемая задача является основной задачей выпуклого программирования. Составим функцию Лагранжа и найдем ее частные производные.
выпуклая и ограничения задаются линейными, следовательно вогнутыми, функциями, то рассматриваемая задача является основной задачей выпуклого программирования. Составим функцию Лагранжа и найдем ее частные производные.
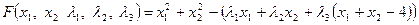 ;
;
 ;
;  ;
;
 ;
;  ;
; 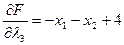 .
.
Случай 1. x 1>0 и х 2>0. Тогда из условия  следует, что
следует, что
 и
и  .
.
Так как
 ,
,  ,
, 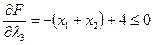 ,
,
то из условий
 , l 1 ³ 0, l 2 ³ 0, l 3 ³ 0
, l 1 ³ 0, l 2 ³ 0, l 3 ³ 0
следует, что l 1 = l 2 = 0,
и так как
x 1 ¹ 0 и x 2¹0, 2 x 1 - l 1 + l 3 = 0 и 2 x 2 - l 2 - l 3 = 0, то l 3 ¹ 0. Следовательно, . Из системы уравнений
. Из системы уравнений

следует, что х 1 = х 2 = 2, l 3 = 4. Так как все условия минимума целевой функции выполняются, то f min = f (2; 2) = 22 + 22 = 8.
Случай 2. х 1 = 0, х 2 ³ 4. Тогда из условий
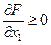 ,
,  ,
, 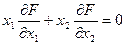
следует, что
 , т.е. 2 х 2 - l 2 - l 3=0.
, т.е. 2 х 2 - l 2 - l 3=0.
Так как
 ,
,  ,
, 
и 0 = l 1×0 + l 2(- х 2) + l 3(- х 2 + 4) = 0, и 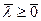 , то l2 = 0 и тогда
, то l2 = 0 и тогда 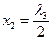 . Следовательно, l 3 ¹ 0,
. Следовательно, l 3 ¹ 0,  и l 3 = 8, х 2 = 4. Но f (0; 4) = 02+42 = 16 > f (2; 2) = 8.
и l 3 = 8, х 2 = 4. Но f (0; 4) = 02+42 = 16 > f (2; 2) = 8.
Случай 3. х 1 ³ 4, х 2 = 0. Тогда, как и выше получим, что
х 1 = 4, однако f (4; 0) = 42 + 02 = 16 > f (2; 2) = 8.
Рассмотрев три случая, приходим к выводу, что
f min = f (2; 2) = 8.
Этот пример имеет простое графическое решение. Действительно, графиком функции  при условии, что
при условии, что
х 1 ³ 0, х 2 ³ 0, х 1 + х 2 ³ 4 является часть параболоида вращения, лежащая в первом октанте перед вертикальной плоскостью
х 1 + х 2 = 4, (рис. 8.) при этом ее самой нижней точкой является точка М(2; 2; 8). Поэтому f min = f (2; 2) = 8 при выполнении данных условий - неравенств.
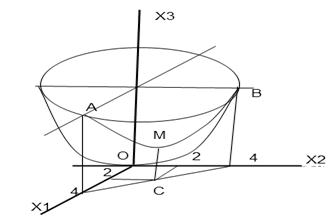
Рис. 3.7. Геометрический метод.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 666; Нарушение авторских прав?; Мы поможем в написании вашей работы!