Методом динамического программирования

Тема 4.2. Примеры решения оптимизационных задач

Методами динамического программирования решаются многие практические задачи: о замене оборудования, оптимальном управлении ресурсами, о наиболее дешевом или наиболее коротком пути завоза товаров потребителям, целочисленного программирования и т. д. Рассмотрим одну из них.

Задача об оптимальном распределении капиталовложений

Планируется распределение начальной суммы капитала (с) между n предприятиями. Предполагается, что выделенные k – тому предприятию в начале периода средства х приносят доход g_k (x)

(k = 1, 2, ¼, n). Будем считать, что: 1) доход, полученный от вложения капитала (средств) в одно предприятие, не зависит от того, какой доход получен другими предприятиями; 2) доход, полученный от различных предприятий, выражается в одинаковых единицах; 3) общий доход равен сумме доходов, полученных от распределения всех средств по всем предприятиям;

4) чем больше средств вкладывается в предприятие, тем больше прибыль.

Рассматривая n -шаговый процесс распределения средств, мы приходим к основным функциональным уравнениям Беллмана:

где: - F_n (c) – общий наибольший доход от вложения капитала (c) в (п) предприятий;

- F_{n -1}(c - x) – наибольший общий доход от вложения капитала (c - x) в (n -1) предприятий;

- g_n (x) – доход от вложения капитала (х) в п -ое предприятие.

Покажем, как пользоваться этими уравнениями при решении конкретных примеров.

Пример. Распределить 120 тысяч рублей порциями, кратными 40 тыс. рублям, между тремя предприятиями (№ 1, № 2, № 3) так, чтобы получить наибольшую прибыль, если прибыль предприятий в зависимости от вложенного капитала выражается таблицей:

Таблица 4.1

Размер вложения, х, тыс. руб.	Прибыль gi (x) по предприятиям
№1	№2	№3

Решение. Для решения примера будем использовать уравнения Беллмана.

F ₃(с) = 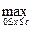(g ₃(x) + F ₂(с-x)); F ₁(x) = g ₁(x).

F ₁(40) = g ₁(40) = 20, F ₁(80) = g ₁(80) = 30,

F ₁(120) = g ₁(120) = 35.

F ₂ (40) = (g ₂(x) + F ₁(40- x) = max(g ₂(0) + F ₁(40);

g ₂(40) + F ₁(0))= max(0+20; 10+0) = 20.

F ₂(80) = (g ₂(x) + F ₁(80 - x)) = max (g ₂(0) + F ₁(80);

g ₂(40)+ F ₁(40); g ₂(80) + F ₁(0)) = max(0+30; 10+20; 35+0) =35. F ₂(120) = 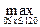(g ₂(x) + F ₁(120- x)) = max(g ₂(0) + + F ₁(120);

g ₂(40) + F ₁(80); g ₂(80) + F ₁(40); g ₂(120) + F ₁(0)) = max(0+35; 10+30; 35+20; 40+0) = 55.

F ₃(40) = (g ₃(x) + F ₂(40- x)) = max(g ₃(0) + F ₂(40); g ₃(40)+ F ₂(0))= max(0+20; 15+0) = 20.

F ₃(80) = (g ₃(x) + F ₂(80- x)) = max(g ₃(0) + F ₂(80);

g ₃(40)+ F ₂(40); g ₃(80)+ F ₂(0))=max(0+35; 15+20; 30+0)= 35.

F ₃(120) = 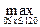(g ₃(x) + F ₂(120-x)) = max(g ₃(0) + F ₂(120);

g ₃(40) + F ₂(80); g ₃(80) + F ₂(40); g ₃(120) + F ₂(0)) = max(0+55; 15+35; 30+20; 45+0) = 55 – искомая наибольшая прибыль.

Из проведенных вычислений видим, что

55= g ₃(0) + F ₂(120)= g ₃(0) + g ₂(80) + F ₁(40)= g ₃(0) + g ₂(80) + g ₁(40).

Таким образом, чтобы получить наибольшую прибыль, равную 55 тыс. руб., надо из имеющихся 120 тыс. руб. предприятию №1 выделить 40 тыс. руб., а предприятию №2 – 80 тыс. руб.

Все вычисления можно значительно упростить, воспользовавшись следующей расширенной таблицей:

Таблица 4.2

x	g 1	F 1	g 2	F 2	g 3	F 3
					0
	20	20
	30		35		30
				55

Известные нам значения для x, g ₁, F ₁, g ₂, g ₃ в эту таблицу записываем сразу. Значения для F ₂, F ₃ вносим в таблицу по мере вычисления. Чтобы вычислить F ₂(40), надо по колонке F ₁ двигаться от 0 до 20 вниз, а по колонке g ₂ двигаться вверх от числа 10 до числа 0, образовывая суммы: 0 + 10, 20 + 0. Наибольшая из них равна 20 = F ₂(40).

Чтобы получить F ₂(80), надо по колонке F ₁ двигаться вниз от числа 0 до числа 30, а по колонке g₂ двигаться вверх от числа 35 до числа 0, образовывая суммы: 0 + 35, 20 + 10, 30 + 0. Наибольшая из них равна: 35 = F ₂(80). Аналогично находим F ₂(120) = 55. Чтобы получить F ₃(120), надо двигаться по колонке F ₂ от 0 вниз до числа 55, а по колонке g ₃ надо двигаться от числа 45 до числа 0 вверх, образовывая суммы: 0 + 45, 20 + 30, 35 + 15, 55 + 0. Наибольшая из них равна 55 = F ₃(120). Пользуясь таким методом, находим остальные элементы таблицы, при этом число, записанное в нижнем правом углу таблицы, равно наибольшей прибыли, полученной от вложения всех средств. Как распределились при этом средства по предприятиям легко увидеть по таблице, подчеркивая слагаемые соответствующих максимальных сумм, перемещаясь из конца таблицы в начало.

Пример. Распределить 200 тыс. руб. по четырем предприятиям порциями, кратными 50 тыс. руб., так, чтобы общая прибыль была наибольшей, если прибыль по каждому предприятию в зависимости от вложенных средств задана таблицей:

Таблица 4.3

Размер вложенных средств, х.	Прибыль g i(x) по предприятиям
	№1	№2	№3	№4

Решение этого примера осуществим устно, применяя расширенную таблицу:

Таблица 4.4

x	g1	F 1	g 2	F 2	g 3	F 3	g 4	F 4
			0
	10	10	5	10	15
	15					25	22
								47

Из полученной таблицы имеем: 47 = F ₃(100) + g ₄(100) = F ₂(50) + g ₃(50) + g ₄(100) = g ₁(50) + g ₂(0) + g ₃(50) + g ₄(100).

Таким образом, наибольшая прибыль равна 47 тыс. руб. Чтобы ее получить, надо первому и третьему предприятию выделить по 50 тыс. руб., а четвертому предприятию выделить оставшиеся 100 тыс. руб.

РАЗДЕЛ 5. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ

Принятие решений в условиях определенности характеризуется тем, что между принятым решением и его результатом существует однозначная (детерминированная) связь. Другими словами каждому варианту решений минуя условия ставится в соответствие его результат (число). По существу, в этом случае мы имеем дело с задачей нахождения оптимального значения скалярной функции нескольких аргументов, которая решается методами дифференциального исчисления и математического программирования. Такого рода задачи мы уже рассматривали выше, в этом разделе мы сделаем акцент на критерии принятия решений.

Дата добавления: 2014-10-31