Тема 5.3. Критерий Лапласа

Тема 5.2. Минимаксный (максиминный) критерий

Этот критерий выражает пессимистическую позицию лица, принимающего решение.:

Rмм = ,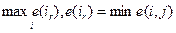

или Rмм = .

В первом случае e(i,j) – «выгода» («выигрыш», «польза» и тому подобное), во втором случае e(i,j) –«потеря» («вред», «проигрыш» и тому подобное).

Этот критерий применяется когда состояния реализуются только один раз, нет даже вероятностных оценок состояний.

Пример. Используяминимаксный (максиминный) критерий найти оптимальную стратегию по данной матрице выигрышей (проигрышей)

Таблица 5.2

	F(1)	F(2)	F(3)	F(4)
Е(1)
Е(2)
Е(3)

Решение.

Rмм = , или

Rмм = .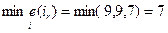

В случае «выигрыша» оптимальными вариантами (решениями) являются Е(1) и Е(3), и в случае «проигрыша» оптимальными вариантами являются Е(1) и Е(3).

Этот критерий опирается на «принцип недостаточности основания», согласно которому все состояния «природы» считаются равновозможными. Для каждой строки таблицы вычисляется среднее арифметическое значение элементов строки 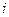. Среди них выбирается наибольшее или наименьшее значение, которому будет соответствовать оптимальное решение.

Пример. Найти оптимальное решение, если матрица «выигрышей» имеет вид

Таблица 5.3

		S	S	S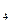
R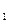
R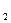
R

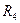
Решение. Всего имеется 4 состояния «ПРИРОДЫ» И 4 возможных решений. Находим среднее арифметическое «выигрышей» для каждой из трех стратегий.

R;

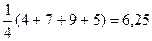R;

R;

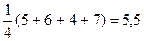R;

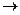
Наибольшее из полученных чисел равно 6,5, поэтом R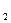является оптимальной стратегией. Если матрицу //V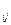// интерпретировать как матрицу затрат, то Rи 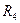будут оптимальными стратегиями.

Дата добавления: 2014-10-31