Тема 7.1. Антагонистические игры

Простейшим видом игры является игра двух лиц с нулевой суммой (сумма выигрыша сторон равна нулю, т. е. выигрыш одного равен проигрышу другого).

Пусть игрок А выбирает одну из стратегий А_i (i = 1, 2,¼, m), а игрок В выбирает одну из стратегий В_j (j = 1, 2, ¼, n), причем каждый выбор делается при полном незнании выбора другого игрока. Выигрыш игрока А будет некоторой функцией j(А_i,В_j),зависящей от выбранных стратегий. Пусть j(А_i,В_j) = h_ij. Составим матрицу выигрышей:

Сделать ход для игрока А означает выбрать одну из строк, а для игрока В - выбрать один из столбцов матрицы H.

Выбрав i - ю строку, игрок А при самом хорошем ходе игрока В получит выигрыш, равный величине min h_ij. Значит, стратегия

для игрока А будет оптимальной, если он будет делать ходы так, чтобы получить выигрыш не менее величины a = (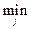h_ij). Величина a называется нижней ценой игры. Игрок В, выбрав

j - й столбец, при самом хорошем ходе игрока А допускает проигрыш, равный величине max h_ij. Стратегия игрока В будет оптимальной, если он будет делать ходы так, чтобы проиграть не более величины b = h_ij). Величина b называется верхней ценой игры. Выигрыш V удовлетворяет неравенству a£V£b, если игроки применяют оптимальные стратегии. Рассмотренные оптимальные стратегии игроков А и В называются соответственно максиминной и минимаксной.

Если a = b, то игра называется вполне определенной. В этом случае V = h_ij, где h_ij - элемент матрицы H, который является одновременно минимальным в строке i и максимальным в столбце j (он называется седловой точкой матрицы).

Решить матричную игру - значит найти оптимальные стратегии игроков и цену игры.

Пример. Решить игру, заданную матрицей:

H =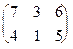

Решение. Так как матрица H имеет седловую точку h₁₂=3, то цена игры равна 3, при этом игрок А должен выбрать первую строку, а игрок В должен выбрать второй столбец. Отклонение от указанной стратегии приводит к уменьшению выигрыша игрока А или увеличению проигрыша игрока В.

Теперь рассмотрим случай отсутствия седловой точки в матрице выигрышей H. В этом случае a < b. Применение максиминной и минимаксной стратегий обеспечивает выигрыш одного не менее величины a и проигрыш другого не более величины b.

Для каждого игрока естественен вопрос увеличения выигрыша (уменьшения проигрыша). Поэтому игроки применяют

не одну, а несколько стратегий. Например, выбор стратегий (строк, столбцов) можно осуществлять случайным образом, определив вероятность выбора каждой строки и каждого столбца.

Пусть i - я строка выбирается игроком А с вероятностью х_i (i = 1, 2, ¼, m), а j - й столбец выбирается игроком В с вероятностью y_j (j = 1, 2, ¼, n). Так как одна из строк и один из столбцов будут обязательно выбраны (каждый игрок обязан сделать ход), то

Цена игры V определяется как математическое ожидание величины, т.е.

V =

Если игрок А выбрал оптимальную стратегию (т.е. наилучшим образом каждой строке поставил в соответствие вероятность ее выбора), то его выигрыш должен быть не меньше цены игры, т.е.

V £

Аналогично применение игроком В оптимальной стратегии должно обеспечить ему проигрыш, не превышающий цену игры, т.е.

V ³

Покажем, что решение матричной игры в рассматриваемом случае можно свести к решению задачи линейного программирования.

Если игрок А применяет оптимальную стратегию

Х = (х₁, х₂, ¼, х_n), то выполняются неравенства:

х₁h₁₁ + x₂h₂₁ + ¼+x_m h_m1³ V,

x₁h₁₂ + x₂h₂₂ +¼ + x_m h_m2 ³ V,

.......................

x₁h_1n + x₂h_2n + ¼ + x_m h_mn³ V.

Каждое из неравенств почленно поделим на V (V> 0), получим систему:

t₁h₁₁ + t₂ h₂₁ + ¼ + t_mh_m1 ³ 1,

t₁h₁₂ + t₂h₂₂ + ¼ + t_mh_m2 ³ 1,

.......................

t₁h_1n + t₂h_2n + ¼ + t_mh_mn ³ 1,

где t_i = x_i / V (i = 1, 2, ¼, m), при этом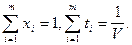

Решение игры требует для игрока максимизировать величину V, значит необходимо минимизировать величину f =.

Таким образом, пришли к задаче линейного программирования, в которой требуется минимизировать линейную функцию f =при условии, что величины t_i неотрицательные и удовлетворяют системе линейных неравенств.

Если игрок В применяет оптимальную стратегию

У = (у₁, у₂, ¼, у_n), то выполняются неравенства:

y₁h₁₁ + y₂h₁₂ + ¼ + y_nh_1n £ V,

y₁h₂₁ + y₂h₂₂ + ¼ + y_nh_2n £ V,

.......................

y₁h_m1 + y₂h_m2 + ¼ + y_nh_mn £ V.

Каждое из неравенств почленно поделим на V (V> 0), получим систему:

u₁h₁₁ + u₂h₁₂ + ¼ + u_nh_1n £ 1,

u₁h₂₁ + u₂h₂₂ + ¼ + u_nh_2n £ 1,

.......................

u₁h_m1 + u₂h_m2 + ¼ + u_nh_mn £ 1,

где u_j = при этом

Решение игры требует для игрока В минимизировать величину V, значит необходимо максимизировать величину L = .

Таким образом, снова пришли к задаче линейного программирования (она является двойственной для первой), в которой требуется максимизировать линейную функцию L = при условии, что переменные величины u_j неотрицательные и удовлетворяют системе линейных неравенств.

Пример. Решить игру, заданную матрицей:

H = .

Решение. Находим нижнюю и верхнюю цены игры:

a = ,

b =

Так как a ¹ b, то матрица не имеет седловой точки. Пусть j - тый столбец выбирается с вероятностью у_j (j = 1, 2, 3). Тогда имеем систему неравенств:

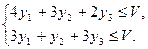
Поделив каждое неравенство системы на V и обозначив у_j / V через u_j, приходим к системе неравенств:

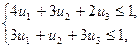
для которой L = u₁ + u₂ + u₃ = . Надо найти такое решение

системы, для которого L принимает наибольшее значение. Решение находим симплексным методом с помощью таблиц:

Таблица 7.1 Таблица 7.2

	u1	u2	u3				u4	u2	u3
u4						u1	1/4	3/4	2/4	1/4
u5						u5	-3/4	-5/4	6/4	1/4
	-1	-1	-1				1/4	-1/4	-2/4	1/4

Таблица 7.3 Таблица 7.4

	u4	u2	u5				u4	u1	u5
u1	3/6	7/6	-2/6	1/6		u2	3/7	6/7	-2/7	1/7
u3	-3/6	-5/6	4/6	1/6		u3		5/7		2/7
		-4/6	2/6	2/6			2/7	4/7	1/7	3/7

Из последней таблицы видим, что u₁ = 0, u₂ = u₃ =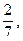

L_max =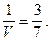

Значит,

Таким образом, цена игры и оптимальная стратегия игрока В найдена.

Пусть i - тая строка выбирается с вероятностью х_i (i = 1, 2). Тогда имеем систему неравенств:

Поделив каждое из неравенств на V и обозначив х_i / V через t_i, приходим к системе неравенств:

для которой f = t₁ + t₂ = Пользуясь соответствием:u₄ «t₁,

u₅ «t₂, из последней строки таблицы 7.4 находим значение t₁ и t₂, при которых f принимает наименьшее значение. Таким образом,

t₁ =

Ответ: Цена игры равна 7/3. Чтобы средний выигрыш игрока А был не меньше7/3, он должен выбирать первую строку с вероятностью 2/3 а вторую строку - с вероятностью 1/3 Чтобы средний проигрыш игрока В был не более7/3, он должен выбирать первый столбец с вероятностью 0, второй - с вероятностью 1/3 третий - с вероятностью 2/3.

Пример. Предприниматель с целью получения прибыли решил свободные средства вложить в акции трех акционерных обществ: “Альфа”, “Бета”, “Гамма”. В условиях нестабильной экономики, когда доходность зависит от степени риска, неплатежа, ликвидности, налогообложения, инфляционных ожиданий

и т.д. он обратился к экономистам, которые дали прогноз доходности в зависимости от трех рыночных ситуаций в стране:

Таблица 7.5

	стратегия рынка стра тегия предпри- нимателя	I	II	III
	Вложения в АО “Альфа”	5%	4%	3%
	Вложения в АО ”Бета”	3%	2%	4%
	Вложения в АО “Гамма”	4%	5%	3%

Найти оптимальную стратегию предпринимателя, которая обеспечила бы ему наибольшую прибыль.

Дата добавления: 2014-10-31