Тема 5.4. Многокритериальные задачи. Парето-оптимальность

На практике часто исход принятого решения оценивается не по одному, а по нескольким критериям, т.е. по векторному критерию. Например, легковой автомобиль должен быть красивым, экономичным, легко управляемым, дешевым, быстро набирать скорость и т.д. Ясно, что оптимальность решения по одному из критериев скорее всего не будет оптимальным по другому критерию. Более того, один критерий может противоречить другому критерию (дешевым, суперсовременным). ЛПР надо с самого начала разумно подойти к подбору перечня критериев, сделав его небольшим, не противоречивым, исключить дублирование, убрать малозначительные.

Так как во многих случаях оптимальность результата (принятого по многим критериям) решения в смысле наибольшее или наименьшее значение невозможна, то применяют другое понятие оптимальности.

Определение. Решение (план) называют эффективным, если не существует решение (план), которое по всем параметрам было бы лучше данного. В этом случае говорят, что решение паретооптимальное.

Множество эффективных решений при векторном критерии {X*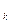}, называемое множеством Парето, определяется следующим образом:

,

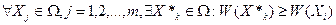причем, хотя бы одно из неравенств является строгим, где W – критерий (показатель).

Рассмотрим пример. Предположим, что нас интересуют два показателя продукции: W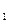- объем производства продукции и W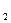- качество продукции. Каждому допустимому варианту соответствует на плоскости координат точка 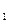(W,W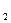). Множество этих точек составляют область допустимых решений (она показана на рисунке). Очевидно, внутренние точки этой области не являются оптимальными по Парето, следовательно решение находится на границе. В частности, все точки дуги АВ («северо-восточная граница») образуют эффективное по Парето множество. Так как задача отыскания паретооптимальных решений в общем случае не решена, то такие решения находят используя дополнительную информацию.

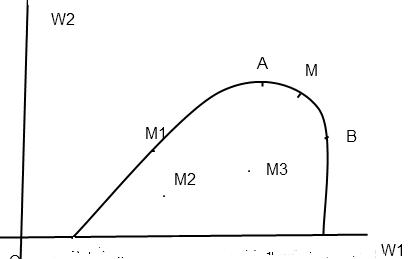
Рис. 5.1. Множество парето-оптимальных решений

Обычно дополнительная информация содержит ранжирование критериев в порядке предпочтения или задание весов критериям. Например, можно применить следующую форму свертки критериев:

W(X) = ,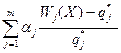

где:

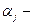вес j-го критерия,

,

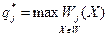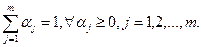
При решении многокритериальных задач можно применить понятие «полезность». Под полезностью понимают некоторую скалярную величину u(x), обладающую следующими свойствами:

1. Если вариант 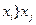(вариант 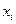предпочтительнее варианта 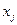), то ;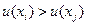

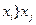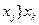2. Если и , то 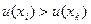- транзитивность;

3. 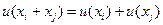- аддитивность.

РАЗДЕЛ 6. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

Дата добавления: 2014-10-31