
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод «покоординатного спуска»
|
|
|
|
Тема 3.6. Численные методы оптимизации
Идея метода. Пусть требуется найти приближенно безусловный минимум функции многих аргументов Ф(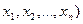 . Для этого выбирают произвольно точку М
. Для этого выбирают произвольно точку М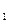 желательно поближе к точке предполагаемого минимума М
желательно поближе к точке предполагаемого минимума М . Далее, изменяют одну любую из координат на произвольную величину
. Далее, изменяют одну любую из координат на произвольную величину  . Получают точку М
. Получают точку М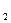 и вычисляют значение Ф(М
и вычисляют значение Ф(М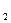 ), которая представляет собой функцию одного аргумента
), которая представляет собой функцию одного аргумента  .Далее, решают уравнение Ф′(М
.Далее, решают уравнение Ф′(М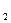 ) = 0 и находят значение
) = 0 и находят значение  , при котором
, при котором
Ф(М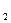 ) имеет наименьшее значение. Затем от точки М
) имеет наименьшее значение. Затем от точки М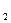 переходят к точке М
переходят к точке М , изменяя в М
, изменяя в М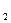 на величину
на величину  только одну другую координату. Вычисляют значение Ф(М
только одну другую координату. Вычисляют значение Ф(М ), которая представляет собой функцию одного аргумента
), которая представляет собой функцию одного аргумента  .Далее, решают уравнение Ф′(М
.Далее, решают уравнение Ф′(М ) = 0 и находят значение
) = 0 и находят значение  , при котором Ф(М
, при котором Ф(М ) имеет наименьшее значение. Затем от точки М
) имеет наименьшее значение. Затем от точки М переходят к точке М
переходят к точке М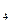 , изменяя в М
, изменяя в М на величину
на величину  только одну другую координату и так далее. В результате получают последовательность Ф(М
только одну другую координату и так далее. В результате получают последовательность Ф(М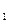
 Ф(М
Ф(М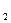 ), Ф(М
), Ф(М ),…, которая при известных условиях сходится к Ф(М
),…, которая при известных условиях сходится к Ф(М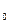 ).
).
Пример. Найти наименьшее значение функции 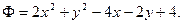
Решение.  - начальная точка вычислительного процесса и
- начальная точка вычислительного процесса и  - произвольное число. От этой точки переходим к точке
- произвольное число. От этой точки переходим к точке  . Ф(
. Ф( , Ф′(
, Ф′( = 0,
= 0,  Тогда получаем точку
Тогда получаем точку  . Переходим к точке
. Переходим к точке 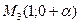 . Ф(
. Ф( ,Ф′(
,Ф′(
 Тогда получаем точку
Тогда получаем точку  . Таким образом, Ф
. Таким образом, Ф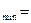 Ф(1;1) = 1.
Ф(1;1) = 1.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 316; Нарушение авторских прав?; Мы поможем в написании вашей работы!