Решение. Тема 3.3. метод множителей Лагранжа

Тема 3.3. метод множителей Лагранжа

Этот метод основан на применении частных производных и применяется для поиска оптимальных значений нелинейной функции при условии, что ее аргументы связаны несколькими уравнениями, которые называют условиями. По этой причине экстремум функции называют условным.

Пример. Найти наименьшее значение функции

Z = x ² + y ² - 2 y + 1, если х + у – 4 = 0.

Рис. 3.5. Условный экстремум.

Плоскость х + у – 4 = 0 пересекает параболоид вращения

z = x ² + y ² - 2 y + 1

по параболе АСВ. Нижняя ее точка С будет соответствовать условному минимуму.

Из уравнения х + у – 4 = 0 выразим (у) через (х) и подставим в функцию z = x ² + y ² - 2 y + 1. Получим функцию одного аргумента

z = x ² + (4- x)² - 2(4- x) +1 = 2 x ² - 6 x + 9.

Точку условного минимума находим из уравнения

z ¢ = (2 x ² - 6 x + 9)¢ = 0.

Получаем: 4 х – 6 = 0, . Тогда

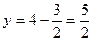и .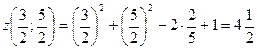

Таким образом условный минимум функции равен и он достигается в точке М.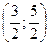

В общем виде задача на условный экстремум формулируется так: найти оптимальное значение функции

f = f (x ₁, x ₂,…, x_n), если ее аргументы удовлетворяют системе уравнений

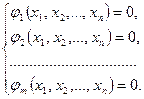
Система уравнений не должна быть противоречивой, иначе задача не имеет решения. Если система имеет единственное решение М ₀, то f _max = f _min = f (M ₀). Для того, чтобы f _max ¹ f _min необходимо существование более одного решения. Чтобы решений было не одно, обычно количество уравнений (условий) берут меньше количества аргументов (т < п).

Далеко не всегда при решении таких задач можно поступить, как в рассмотренном выше примере, т.е. найти общее решение системы уравнений, подставить его в исходною функцию и решить обычную задачу на экстремум функции одного или нескольких аргументов. Для решения задач на условный экстремум существует универсальный метод множителей Лагранжа.

Рассмотрим этот метод в случае оптимизации функции двух аргументов z = f (x; y) при одном условии j (х, у) = 0. Из этого условия следует, что у = y (х), при этом функция y может быть и неизвестной, ведь не всегда неявную функцию можно сделать явной. Функция z = f (x; y) является сложной функцией одного ар аргумента (х). По правилу дифференцирования сложной функции имеем: 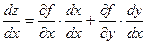. В точке возможного экстремума 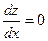. Поэтому .

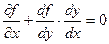Но , поэтому .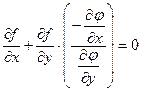

Положим 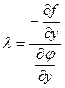. Тогда в точке условного экстремума выполняются равенства: j (х, у) = 0, ,

а также равенство (так как в наших рассуждениях (х) и (у) взаимно заменяемы). Составим вспомогательную функцию

F (x, y, l) = f (x, y) + l (x, y)

(она называется функцией Лагранжа, число l называется множителем Лагранжа). Если найти ее частные производные

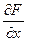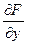, , и приравнять их к нулю, то получим те же самые три равенства, которые являются необходимым условием существования экстремума функции F (x, y, l) и условного экстремума функции f (x, y).

Пример. Найти экстремум функции Z = 4 x ² + y ² + 1, если

х + у = 1.

Решение. Составляем функцию Лагранжа.

F (x, y, l) = 4 x ² + y ² + 1 + l (х + у -1).

Находим ее частные производные и приравниваем их к нулю.

, , .

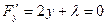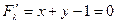Тогда:

; ; ; .

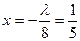Таким образом – точка возможного условного экстремума. Но так как система

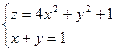
определяет «восходящую» параболу, то –

условное наименьшее значение функции.

В общем случае функция Лагранжа имеет вид:
F = f (x ₁, x ₂,…, x_n) + l ₁ j ₁(x ₁, x ₂,…, x_n) + …+ l_mj_m (x ₁, x ₂,…, x_n)

и для нахождения точки возможного условного экстремума надо решать систему уравнений:

, , , .

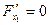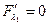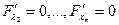Если нет уверенности, что найденная точка действительно является точкой экстремума, то применяют достаточный признак его существования, который формулируется так: если в задаче на условный экстремум в точке М ₀ возможного экстремума d ² F >0, то М ₀ – точка условного минимума, если d ² F <0, то М₀ – точка условного максимума, при этом d ² F – дифференциал второго порядка функции F.

Пример. Найти экстремум функции f = xy, если х + у – 2 = 0.

Решение. Составляем функцию Лагранжа и находим ее производные.

F = xy + l (x + y - 2), , , .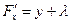

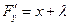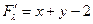Найденные частные производные приравниваем к нулю и решаем систему:

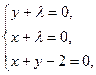
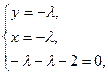
Таким образом М₀(1; 1) – точка возможного экстремума. Находим второй дифференциал функции Лагранжа.

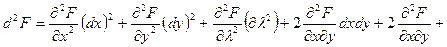
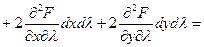0×(dx)²+0×(dy)²+0×(dl)²+2×1× dxdy

+ 2×1× dxdl + 2×1× dydl = 2 dxdy + 2 dl (dx + dy).

Из условия х + у – 2 = 0 следует, что dx + d y = 0, поэтому
d ² F = -2(dx)² + 2 dl ×0 =-- 2(dx)².

Так как d ² F <0, то М (1; 1) – точка условного максимума.

Дата добавления: 2014-10-31