Тема 2.13. Метод Гомори

Нередко в задачах линейного программирования присутствует дополнительно условие целочисленности аргументов целевой функции. Такие задачи можно решать без учета целочисленности и округлять полученный результат до ближайших целых чисел. Но в этом случае не совсем ясно какие погрешности возникают. Геометрическим методом при количестве аргументов не более трех можно точно найти целочисленное оптимальное решение, двигая соответствующим образом опорную прямую или опорную плоскость. Существуют аналитические методы поиска целочисленного оптимального решения, к ним относится метод Гомори.

Рассмотрим метод Гомори для случая четырех аргументов и систем ограничений, состоящей из двух уравнений.

F = c ₁ x ₁ + c ₂ x ₂ + c ₃ x ₃ + c ₄ x ₄,

x_i ³0, x_i – целое, f_max =?

сначала решаем эту задачу, отбрасывая условия целочисленности симплексным методом. По последней симплексной таблице составляем систему уравнений. Пусть она имеет вид:

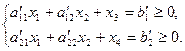
Эта система равносильна исходной системе уравнений и Х ^*(0; 0; ;) – оптимальный план. Если при этом , – целые числа, то этот план будет оптимальным и для исходной целочисленной задачи.

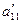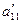Пусть, например, – дробное число. Тогда = [] + b ₁, = [] + a ₁₁, = [] + a ₁₂, где [], [], [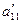] – целые части соответствующих чисел. Напомним, что целая часть числа, есть ближайшее целые число, не превышающее это число.

Подставим выражения коэффициентов в уравнения системы. Получим:

[]+ b ₁,

a ₁₁ х ₁+ a _{1 2} х ₂- b ₁=[]-[]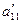 х ₁-[] х ₂- х ₃.

Рассмотрим неравенство a ₁₁ х ₁+ a _{1 2} х ₂- b ₁³0 (оно называется неравенством Гомори).

Покажем, что любой целочисленный план Х ¢ исходной задачи удовлетворяет неравенству Гомори.

Допустим противное, т.е. a ₁₁+ a _{1 2} - b ₁ <0. Положим, a ₁₁+ a _{1 2} = g. Так как ³0, ³0, a ₁₁³0, a ₁₂³0, то g³0.

Вместе с тем 0< b ₁<1 и g < b ₁. Тогда 0£ g < b ₁<1. Значит

g - b ₁ = a ₁₁+ a ₁₂- b ₁ – дробное число. Но оно равно числу []--[]-[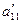]-, которое является целым. Получили противоречие. Таким образом, всякое целочисленное решение удовлетворяет неравенству Гомори.

Следует отметить, что нецелочисленный план исходной задачи не удовлетворяет неравенству Гомори, в противном случае имеем: a ₁₁×0 + a ₁₂×0 - b ₁ =- b ₁ ³ 0, т.е. b ₁ £ 0, что невозможно по определению дробной части не целого числа .

Рассматриваем новую задачу, которая отличается от исходной добавлением в нее неравенства Гомори, которое отсекает часть нецелочисленных планов, не затрагивая целочисленные планы исходной задачи. Новую задачу решаем симплексным методом и если не получаем целочисленный оптимальный план, то процесс решения продолжаем аналогичным образом.

Следует отметить, что дробными могут быть несколько коэффициентов , в этом случае выбирается тот, у которого наибольшая дробная часть.

Пример. Найти наибольше значение функции f = 3 х ₁ + 16 х ₂, если х ₁, х ₂ – целые неотрицательные числа.

Дата добавления: 2014-10-31