Тема 2.10. Двойственные задачи линейного программирования

Задача 1. Предприятие производит два вида товаров

(А и В). На их производство оно затрачивает три вида сырья (I,II,III), запасы которых составляют 5 ед., 8 ед., 8 ед. соответственно. На 1 ед. товара А расходуется 1 ед. сырья 1, 2 ед. сырья II, 1 ед. сырья III.

На производство 1 ед. товара В расходуется 1 ед. сырья I,

1 ед. сырья II, 2 ед. сырья III. Прибыль от реализации 1 ед. товара А составляет 3 денежных единицы, а от реализации 1 ед. товара В - 4 денежных единицы. Найти оптимальный план производства товаров, дающий наибольшую прибыль.

Дадим математическую формулировку этой задачи. Пусть (x, х) - план производства товаров А и В соответственно. Условие производства товаров выражается системой неравенств:

Прибыль выражается функцией f = 3x+4х. Значит, требуется найти такие неотрицательные значения (x, х ), удовлетворяющие системе:

при которых функция f = 3 x ₁ + 4 x ₂ принимает наибольшее значение.

Эта задача определяется матрицей коэффициентов

С =.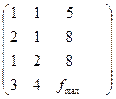

Задача 2. Предположим, что предприятие, о котором шла речь в задаче 1, имеет возможность продать сырье, не производя из него товар. Какую прибыль надо получить от продажи одной единицы каждого сырья, чтобы прибыль от продажи сырья была не меньше прибыли от реализации товара, изготовленного из него.

Обозначим через у₁, у₂, у₃ прибыль от продажи одной единицы I, II, III сырья соответственно. Прибыль от продажи сырья, необходимого для изготовления 1 ед. товара А, равна 1× у ₁+2× у ₂ +1× у ₃; прибыль от продажи сырья, необходимого для изготовления 1 ед. товара В, равна 1× y ₁ + 1× y ₂ +2× y ₃. По условию задачи прибыль от продажи сырья должна быть не меньше при
были от продажи товара, изготовленного из него. Поэтому имеем систему неравенств:

Прибыль от продажи всего сырья выражается функцией:

Z = 5× y ₁ + 8× y ₂+8× y ₃.

С другой стороны, покупатель не желает переплачивать за сырье и стремится минимизировать свои расходы на сырье, т.е. минимизировать прибыль предприятия, продающего сырье. Следовательно, в задаче 2 требуется найти такие значения неотрицательных величин у ₁, у ₂, у ₃, удовлетворяющих системе неравенств:

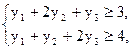
при которых функция Z = 5 y ₁+8 y ₂ +8 y ₃ принимает наименьшее значение.

Задача 2 определяется матрицей:

D =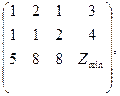

которая получается из матрицы С транспонированием, если учесть, что условие продажи и купли сырья состоит в том, что

f_max = Z_min.

Сформулируем в общем виде две взаимно двойственные симметрические задачи.

Исходная задача

Для неотрицательных значений переменных х ₁, х ₂,..., х_n найти такое решение системы неравенств:

при котором функция f = c ₁ x ₁ + c ₂ x ₂ +...+ c_nx_n принимает наибольшее значение.

Двойственная задача

Для неотрицательных значений переменных у ₁, у ₂,..., у_m найти такое решение системы неравенств:

при котором функция:

Z = b ₁ у ₁ + b ₂ у ₂ +...+ b_m y_m

принимает наименьшее значение.

Любую из этих задач можно считать исходной, тогда другая будет двойственной к ней. Существуют несимметрические двойственные пары задач, однако мы их рассматривать не будем.

Теорема. Если из пары двойственных задач одна обладает оптимальным планом, то и другая обладает оптимальным планом, при этом оптимальные значения целевых функций равны между собой.

Если целевая функция одной из задач не ограничена, то другая задача не имеет решения.

Пример. Для данной задачи составить двойственную.

Z = 8 у ₁ +5 у ₂, Z_min =?

Решение. Исходная задача определяется матрицей:

А =

Составляем транспонированную матрицу:

=

По матрице В записываем двойственную задачу:

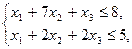
f = 5 х ₁ + 14 х ₂+6 х ₃, f _max =?.

Замечание. Решив одну из двойственных задач, например, на максимум, из последней строки последней симплекс-таблицы можно выписать решение для двойственной задачи. Для этого надо воспользоваться соответствием:

где х_{n +1}, x_{n +2}, ¼, x_n+m – балансовые переменные задачи на максимум, а у_{m +1}, y_{m +2},¼, y_m+n – балансовые переменные двойственной задачи на минимум.

Пример. С помощью двойственной задачи решить задачу на минимум целевой функции

f = 3 x ₁ + 2 x ₂, если х ₁ + 4 х ₂³6, 2 х ₁ + 3 х ₂³7.

Решение. Составляем матрицу H, определяемую задачу на минимум:

.

Путем транспонирования матрицы Н получаем матрицу

.

По матрице Н^Т составляем задачу на максимум.

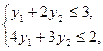z = 6 у ₁ + 7 у ₂® max?.

Решаем задачу на максимум с помощью симплексных таблиц.

Таблица 2.13

	y 1	y 2	y 3	y 4	cв.к
уy 3
уy 4
z	-6	-7

Таблица 2.14

	y 1	y 2	y 3	y 4	сcв.к
y 3
y 2
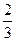
z

, значение х ₁ читаем в нижней строке последней таблицы напротив у ₃, а значение x ₂ читаем в этой же строке напротив у ₄. получаем, что .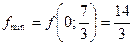

Дата добавления: 2014-10-31