
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2.1. Векторы
|
|
|
|
Вектором называется направленный отрезок и обозначается  или
или 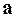 . Вектор характеризуется направлением и модулем (длиной) или координатами.
. Вектор характеризуется направлением и модулем (длиной) или координатами.
Пусть в ортонормированном базисе  начало вектора находится в точке
начало вектора находится в точке  , а конец в точке
, а конец в точке  . Тогда координаты вектора
. Тогда координаты вектора 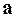 определяются по формуле:
определяются по формуле:
 . (2.1)
. (2.1)
Модуль вектора 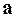 в базисе
в базисе  вычисляется по формуле
вычисляется по формуле
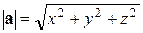 . (2.2)
. (2.2)
Над векторами  и
и 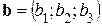 можно совершать следующие линейные операции:
можно совершать следующие линейные операции:
– сложение (вычитание): 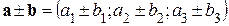 ;
;
– умножение вектора на число: 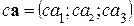 , где
, где  – некоторое число.
– некоторое число.
Скалярным произведением двух векторов 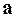 и
и  называется число, обозначаемое символом
называется число, обозначаемое символом  , и удовлетворяющее условиям:
, и удовлетворяющее условиям:
1) 
2)  ;
;
3) 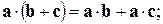
4) 
Линейное пространство, в котором введено скалярное произведение, называют Евклидовым.
Длиной или нормой любого вектора 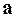 называют арифметическое значение корня квадратного из скалярного квадрата
называют арифметическое значение корня квадратного из скалярного квадрата 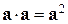 :
:
 .
.
Угол между векторами определяется как угол, изменяющийся в пределах от 0 до  радиан (от
радиан (от  до
до  ). Косинус угла между векторами
). Косинус угла между векторами 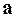 и
и  вычисляется по формуле
вычисляется по формуле
 (2.3)
(2.3)
откуда следует:  .
.
Векторы 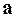 и
и  называются ортогональными, если угол между ними равен
называются ортогональными, если угол между ними равен 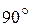 . Условие ортогональности векторов
. Условие ортогональности векторов 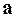 и
и  : если их скалярное произведение равно нулю:
: если их скалярное произведение равно нулю: 
Векторы 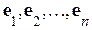 образуют ортонормированный базис линейного пространства, если эти векторы взаимно ортогональны и их длины равны единице:
образуют ортонормированный базис линейного пространства, если эти векторы взаимно ортогональны и их длины равны единице:

Пусть векторы 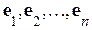 образуют ортонормированный базис линейного пространства. Тогда координаты векторов
образуют ортонормированный базис линейного пространства. Тогда координаты векторов 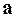 и
и  в этом ортонормированном базисе записывают в виде
в этом ортонормированном базисе записывают в виде
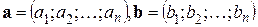 ,
,
а их скалярное произведение и длины векторов принимают наиболее простую форму:
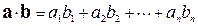 ,
, 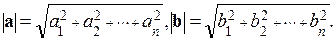 (2.4)
(2.4)
Косинус угла между векторами  и
и 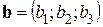 в произвольном ортонормированном базисе
в произвольном ортонормированном базисе 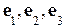 вычисляется по формуле
вычисляется по формуле
 (2.5)
(2.5)
Упорядоченная тройка векторов 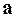 ,
, 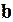 ,
,  с общим началом в точке
с общим началом в точке  называется правой, если кратчайший поворот от вектора
называется правой, если кратчайший поворот от вектора 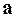 к вектору
к вектору 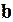 наблюдается с конца вектора
наблюдается с конца вектора  происходящим против хода часовой стрелки (рис.2.1).
происходящим против хода часовой стрелки (рис.2.1).
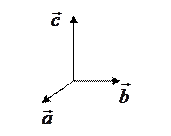
|
| Рис.2.1 |
Векторным произведением векторов 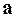 и
и  называется вектор
называется вектор  , обозначаемый как
, обозначаемый как  , который удовлетворяет следующим трем условиям:
, который удовлетворяет следующим трем условиям:
1) ; (2.6)
; (2.6)
2)  и
и  ;
;
3) тройка векторов 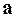 ,
,  ,
, 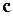 – правая.
– правая.
Если заданы координаты векторов  и
и  в ортонормированном базисе
в ортонормированном базисе  , то их векторное произведение вычисляется по формуле
, то их векторное произведение вычисляется по формуле
 (2.7)
(2.7)
Свойства векторного произведения:
1) 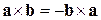 ;
;
2) 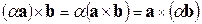 , где
, где 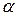 – некоторое число;
– некоторое число;
3)  .
.
Векторы 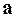 и
и 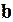 называются коллинеарными, если угол между ними равен 0 или
называются коллинеарными, если угол между ними равен 0 или  радиан (
радиан ( или
или  ), т.е. они лежат на параллельных прямых или на одной прямой. Условие коллинеарности векторов
), т.е. они лежат на параллельных прямых или на одной прямой. Условие коллинеарности векторов 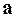 и
и 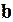 : если существует такое число
: если существует такое число 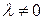 , что
, что 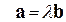 , т.е. соответствующие координаты коллинеарных векторов пропорциональны. Векторное произведение коллинеарных векторов
, т.е. соответствующие координаты коллинеарных векторов пропорциональны. Векторное произведение коллинеарных векторов 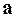 и
и 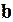 равно нулю:
равно нулю: 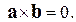
Геометрический смысл векторного произведения: модуль векторного произведения векторов 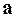 и
и 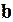 численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 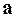 и
и 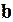 как на сторонах:
как на сторонах:
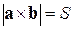 . (2.8)
. (2.8)
Смешанным произведением векторов 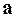 ,
,  ,
, 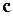 называется число
называется число 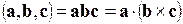 .
.
Если в произвольном правом ортонормированном базисе 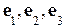 заданы координаты векторов
заданы координаты векторов  ,
, 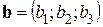 и
и  , то
, то
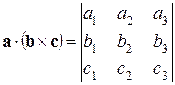 . (2.9)
. (2.9)
Свойства смешанного произведения:
1)  ;
;
2) 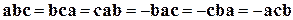 ;
;
3) если , то тройка векторов
, то тройка векторов 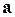 ,
,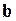 ,
, – правая, если
– правая, если
 – левая;
– левая;
4)  .
.
Векторы 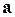 ,
,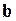
 называются компланарными, если они лежат на параллельных плоскостях или на одной плоскости.
называются компланарными, если они лежат на параллельных плоскостях или на одной плоскости.
Условие компланарности векторов 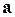 ,
,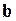 ,
, : три вектора
: три вектора 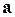 ,
,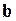 ,
, компланарны тогда и только тогда, когда их смешанное произведение равно нулю:
компланарны тогда и только тогда, когда их смешанное произведение равно нулю: 
Геометрический смысл смешанного произведения: модуль смешанного произведения векторов 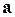 ,
,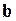 ,
, численно равен объему параллелепипеда, построенного на векторах
численно равен объему параллелепипеда, построенного на векторах 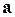 ,
,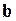 ,
, как на сторонах:
как на сторонах:
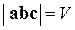 . (2.10)
. (2.10)
Пример 2.1. Даны две точки  ,
,  . Найти координаты вектора
. Найти координаты вектора 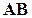 и координаты точки
и координаты точки 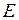 – середины отрезка
– середины отрезка 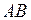 .
.
Решение. По формуле (2.1) получаем 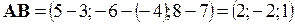 . Пусть
. Пусть 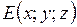 , тогда
, тогда 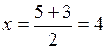 ,
, 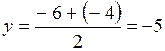 ,
,  . Таким образом координаты точки
. Таким образом координаты точки  .
.
Пример 2.2. Даны два вектора  ,
,  . Найти угол между ними.
. Найти угол между ними.
Решение. По формуле (2.5) получаем
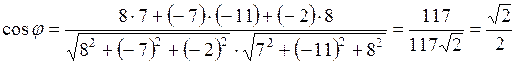 , тогда
, тогда  .
.
Пример 2.3. Доказать, что векторы  ,
, 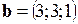 ортогональны.
ортогональны.
Решение. По формуле (2.4) находим:  . Согласно критерию ортогональности векторы
. Согласно критерию ортогональности векторы 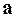 и
и 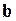 ортогональны.
ортогональны.
Пример 2.4. Даны два вектора  ,
, 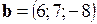 . Найти векторное произведение
. Найти векторное произведение  .
.
Решение. По формуле (2.7) получаем
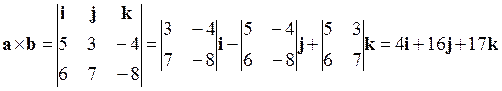 . Следовательно,
. Следовательно,  .
.
Пример 2.5. Вершины треугольника находятся в точках 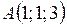 ,
,  ,
, 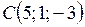 . Вычислить площадь треугольника.
. Вычислить площадь треугольника.
Решение. Используя формулу (2.1), находим координаты векторов 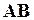 и
и 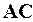 :
:  ,
,  . Далее, по формуле (2.7) определим
. Далее, по формуле (2.7) определим 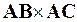 :
:
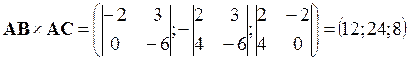 .
.
Тогда 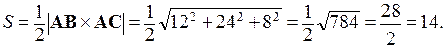
Пример 2.6. Вычислить, при каких значениях 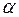 и
и 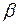 векторы
векторы  и
и 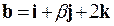 коллинеарны.
коллинеарны.
Решение. Соответствующие координаты коллинеарных векторов пропорциональны, т.е.  , откуда находим
, откуда находим 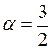 и
и  .
.
Пример 2.7. Найти объем параллелепипеда, построенного на векторах  ,
,  ,
, 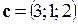 .
.
Решение. По формуле (2.10)  . Используя формулу (2.9), находим:
. Используя формулу (2.9), находим:
 . Следовательно,
. Следовательно, 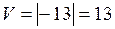 .
.
Пример 2.8. Доказать, что векторы 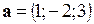 ,
, 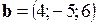 ,
,  компланарны.
компланарны.
Решение. Проверим выполнение условия компланарности. Так как 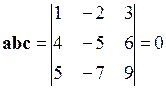 , то можно утверждать, что данные векторы компланарны.
, то можно утверждать, что данные векторы компланарны.
Пример 2.9. Вычислить объем треугольной пирамиды, вершины которой находятся в точках 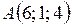 ,
, 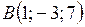 ,
,  ,
, 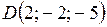 .
.
Решение. Используя формулу (2.1) найдем координаты векторов, на которых построена пирамида: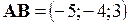 ,
,  ,
,  .
.

Пример 2.10. Выяснить, лежат ли точки  ,
,  ,
,  ,
, 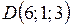 в одной плоскости.
в одной плоскости.
Решение. Используя формулу (2.1) найдем координаты векторов:  ,
,  ,
,  . Теперь проверим выполнение критерия компланарности. Так как
. Теперь проверим выполнение критерия компланарности. Так как 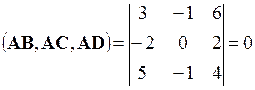 , то векторы компланарны, а значит, точки
, то векторы компланарны, а значит, точки 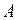 ,
, ,
, 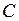 ,
, 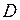 лежат в одной плоскости.
лежат в одной плоскости.
Пример 2.11. Выяснить, правой или левой будет тройка векторов 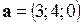 ,
,  ,
, 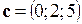 .
.
Решение. Воспользуемся формулой (2.9): 
Согласно свойствам смешанного произведения, знак «–» указывает на то, что вектора 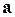 ,
,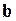 ,
, образуют левую тройку.
образуют левую тройку.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 642; Нарушение авторских прав?; Мы поможем в написании вашей работы!