Постановка задачи фирмы

Поверхность производственных возможностей. Вмененные издержки

Рис. 6.1. Производственное множество

Рассмотрим на рис. 6.1 точки Y ₁, Y ₂. Затраты по этим технологиям одинаковы, а выпуск разный. Производитель, если он не лишен здравого смысла, никогда не выберет технологию Y ₁, раз есть лучшая технология Y ₂.

Для каждого найдем самую высокую точку в производственном множестве. Эта технология самая лучшая.

Для вектора затрат Z обозначим множество . Множество 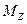– это множество всех возможных выпусков при затратах Z. В этом множестве рассмотрим поверхность производственных возможностей

,

т.е. – это множество лучших выпусков при данных затратах Z. Для любого вектора затрат все наилучшие выпуски лежат на поверхности производственных возможностей.

Пусть p – вектор цен, а – технология, т.е. вектор "затраты - выпуск", то 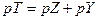– прибыль от использования технологии T.

Производитель выбирает технологию из своего производственного множества, максимизирующую прибыль, т.е. производитель решает следующую задачу:

, . (6.1)

Из (6.1) следует: если цены положительны, что естественно, то компонента "выпуск" решения этой задачи автоматически будет лежать на кривой производственных возможностей.

Выпуск фирмы можно охарактеризовать ПФ. Если цена единицы продукции p, а цена единицы ресурса w, то каждому вектору затрат отвечает прибыль . Если нет других ограничений, то приходим к задаче фирмы:

, . (6.2)

Условия Куна-Таккера для этой задачи (задача нелинейного программирования) имеют вид:

, (6.3)

. (6.4)

Будем предполагать, что все затраты строго положительны, тогда точка экстремума удовлетворяет условиям:

. (6.5)

Соотношение (6.5) дает оптимальное решение задачи фирмы. Экономический смысл соотношения (6.5): в оптимальной точке стоимость предельного продукта данного ресурса должна равняться его цене.

Дата добавления: 2014-10-31