Виды математических моделей САУ

Вопросы для самопроверки

1. Перечислите принципы управления и поясните их.

2. Что представляет собой закон управления?

3. Каково назначение регулятора в системе?

4. По каким признакам классифицируются системы управления?

5. Дайте классификацию систем по виду задающего воздействия.

6. Назовите необходимые и достаточные условия линейности систем.

Что представляет собой система управления? Перечислите основные элементы системы автоматического управления

Раздел 3. ТЕОРИЯ ЛИНЕЙНЫХ И непрерывных СИСТЕМ

Изучаемые вопросы:

· Математические модели;

· Преобразование структурных схем;

· Частотные характеристики;

· Типовые звенья;

· Логарифмическо - частотные характеристики

· Математические модели в форме переменных состояния

Целью математического описания САУ является составление той или иной математической модели, используемой в дальнейшем для анализа и синтеза САУ. Любая математическая модель является, приближением к действительному состоянию взаимодействия отдельных информационных параметров объекта или всей системы в целом и отражает наиболее существенные взаимосвязи между переменными величинами. Так большинство переменных величин объектов и систем управления подвергается ограничению естественным или искусственным путем. Множество зависимостей между информационными параметрами являются нелинейными и должны быть представлены нелинейными математическими моделями. Однако в рамках настоящего пособия рассматриваются линейные математические модели, так как многие режимы функционирования САУ характеризуются незначительными изменениями переменных величин, в пределах которых зависимости между величинами могут считаться линейными. Системы, работающие в полных диапазонах изменений переменных, а также системы, содержащие элементы с явно выраженными нелинейными характеристиками (например, релейными), являются существенно нелинейными системами и рассматриваются в курсе «Нелинейные системы управления».

Различают следующие виды математических моделей САУ:

1) дифференциальные и разностные уравнения систем управления и их элементов;

2) векторно-матричные модели в пространстве состояний;

3) передаточные функции элементов и систем управления;

4) структурные схемы систем управления;

5) направленные графы систем управления;

6) временные характеристики САУ;

7) частотные характеристики САУ.

Эти же виды математических моделей в той или иной мере используются и для описания нелинейных САУ.

Дифференциально-разностные уравнения САУ

Дифференциальные (в частных случаях, алгебраические) уравнения непрерывных систем и разностные уравнения дискретных систем являются основной первичной формой математического описания любой САУ. Они могут использоваться самостоятельно для выполнения задач анализа и синтеза или служить основой для создания других форм математического описания.

Дифференциальные и алгебраические уравнения непрерывных САУ составляются на основании изучения и осознания основных физических, химических и информационных процессов, происходящих в объекте управления и системе в целом. Часто для записи уравнений используются уже известные законы, устанавливающие связь между технологическими переменными величинами.

Рассмотрим, в качестве примера, составление уравнений для двигателя постоянного тока независимого возбуждения, управляемого изменением напряжения, приложенного к якорю. Модель двигателя (рис.2.1) включает якорную цепь, содержащую сопротивление R­ _я и индуктивность L _я якоря с противоэдс якоря E. Питание цепи якоря подается от источника напряжением U. Вал двигателя, вращающийся с угловой скоростью w, соединен с рабочим органом РО, создающим момент сопротивления на валу двигателя.

Уравнение равновесия напряжений электрической цепи якоря двигателя:

U - E = i _Я R _Я + L _Я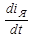 (3.1)

На основании закона электромагнитной индукции противоэдс двигателя:

E = C _e Ф w, (3.2)

где с _е – конструктивный коэффициент; Ф – поток возбуждения, принимаемый постоянным; Ф = const.

В соответствии с законом Ньютона для вращательного движения уравнение движения вала двигателя:

J 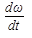= M_g - M­_c, (3.3)

где J – момент инерции движущихся частей двигателя и рабочего органа, приведенных к валу двигателя;

M_g = C_МФi _Я, (3.4)

где C_М – конструктивный коэффициент; M_c - момент сопротивления на валу двигателя. Таким образом, уравнение (3.1 – 3.4) образуют математическую модель двигателя постоянного тока. Два из них (3.1 и 3.3) – дифференциальные уравнения, два другие (3.2 и 3.4) – алгебраические. Все уравнения линейные, так как зависимости E = f (w) и M_g = f (i _Я) суть прямые линии (C_eФ и C_МФ = const), а коэффициенты дифференциальных уравнений (J, R _Я, L _Я, M_e) постоянные.

Преобразование Лапласа

Несмотря на неограниченные возможности компьютерных технологий по решению систем дифференциальных и разностных уравнений преобразование Лапласа остается по-прежнему широко используемым при решении задач анализа и синтеза САУ.

Непрерывным преобразованием Лапласа непрерывной временной функции f (t) называется следующее преобразование

,

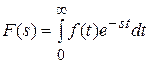где s = a + j w, a и w - постоянные, j = 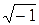. Преобразуемая функция f (t) часто называется оригиналом, а F (s) – изображением функции f (t). К функции f (t) предъявляется требование, чтобы она была однозначной и удовлетворяла условию f (t) = = 0 при t < 0.

Приведем в качестве примеров непрерывного преобразования изображения единичной ступенчатой функции f (t) = 1(t).

.

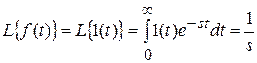Дата добавления: 2014-10-31