Основные свойства преобразования Лапласа

1. Свойство линейности.

Непрерывное преобразование Лапласа являются линейным, т. е. изображение линейной комбинации функций равно линейной комбинации их изображений.

Так если 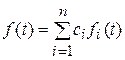, то

.

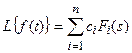2. Изображение смещенной функции (теорема сдвига)

Сдвигу функции оригинала на t, т. е. 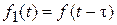соответствует умножение непрерывного изображения на :

.

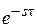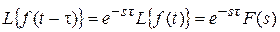3. Изображение производной (конечной разности) n -порядка

Если , то 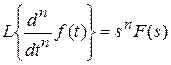, при f (0) = 0 и всех ,
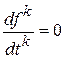k = 1, 2, …, n -1. Другими словами взятию производной n -го порядка соответствует при нулевых начальных условиях умножение изображения на sⁿ.

4. Изображение интеграла (конечной суммы) функции-оригинала

Свойства изменения изображений функции после ее интегрирования или взятия конечной суммы в дискретном варианте является “обратными” по отношению к свойствам дифференцирования или взятия конечных разностей:

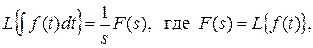
Резюмируя свойства 3 и 4 отметим, что s – оператор дифференцирования в непрерывной области; 1/ s – оператор интегрирования в непрерывной области.

5. Свойство изображения свертываемых функций (теорема свертки)

Сверткой двух непрерывных называется функция, значения которой вычисляются согласно 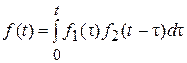для непрерывного времени.

Формулировка свойства об изображении свертки для непрерывного времени:

- изображение свертки равно произведению изображений свертываемых функций.

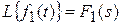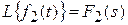Если и , то

.

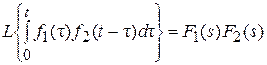6. Определение начального значения функции оригинала по известному изображению

Зная изображение F (s) можно сравнительно просто вычислить начальное и конечное значения функции-оригинала.

Начальное значение непрерывной функции

.

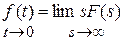6. Конечное значение функции-оригинала

В непрерывном времени .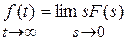

Преобразование дифференциальных и разностных уравнений.

Пусть непрерывная система описывается уравнением

,

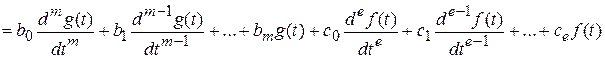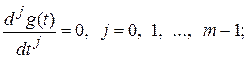
где y (t), g (t), f (t) – выходная управляемая величина, управляющее и возмущающее воздействие соответственно; a ₀, …, a_n; b ₀, …, b_m; c ₀, …, c_e – постоянные коэффициенты. Предположим, что система работает при нулевых начальных условиях, т. е. при t = 0 имеем . Подвергнем заданное дифференциальное уравнение преобразованию Лапласа, используя свойства линейности и изображения производной,

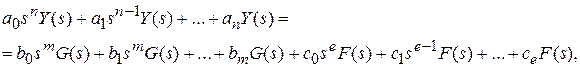
где Y (s), G (s), F (s) – изображения по Лапласу функций y (t), g (t), f (t).

Перепишем полученное уравнение в более сжатой форме

Сравнивая полученное уравнение с исходным, приходим к правилу преобразования по Лапласу любого дифференциального уравнения:

чтобы получить преобразованное по Лапласу уравнение, необходимо операторы дифференцирования заменить комплексными операторами s = a + j w, а все временные функции заменить их изображением.

Отметим, что преобразование по Лапласу уравнение является алгебраическим, что в корне облегчает все математические операции при его использовании.

Теперь возьмем отношения изображений присутствующих в уравнении величин, принимая одну из них (управление G (s) или возмущение F (s)) равной нулю:

.

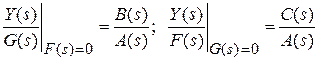Полученные отношения представляют собой передаточные функции системы по управляющему и возмущающему воздействиям:

.

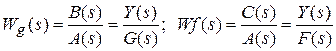Передаточной функцией системы (элемента системы) называется отношение изображений по Лапласу выходной и входной величин при нулевых начальных условиях.

Понятие передаточной функции является одним из фундаментальных в теории автоматического управления и широко используется на различных стадиях анализа и синтеза систем управления.

Дата добавления: 2014-10-31