
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Z-преобразования
|
|
|
|
1. Свойство линейности.
Оба преобразования: непрерывное Лапласа и Z -преобразование, - являются линейными, т. е. изображение линейной комбинации функций равно линейной комбинации их изображений.
Так если 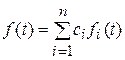 , то
, то
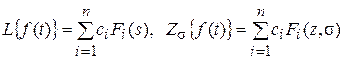 .
.
· Изображение смещенной функции (теорема сдвига)
Сдвигу функции оригинала на t, т. е. 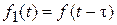 соответствует умножение непрерывного изображения на
соответствует умножение непрерывного изображения на 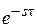 :
:
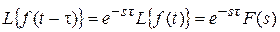 .
.
Если сдвиг t = mT (T - интервал дискретности), то Z – или Z s - изображения функции f (t) умножаются на Z-m
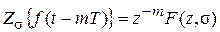 .
.
Частотные случаи последнего свойства:
1) m = +1; 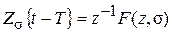 .
.
Т. е. Z -1 – оператор запаздывания на один период дискретности;
2) m = -1; 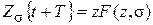 ;
;
Z – оператор опережения на один период дискретности.
· Изображение производной (конечной разности) n -порядка
Если  , то
, то 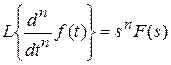 , при f (0) = 0 и всех
, при f (0) = 0 и всех 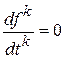 ,
,
k = 1, 2, …, n -1. Другими словами взятию производной n -го порядка соответствует при нулевых начальных условиях умножение изображения на sn.
Аналогично для Z -преобразования (приводим формулировку свойства для s = 0) взятию разности k -го порядка дискретной функции f (nT) соответствует умножение ее изображения на 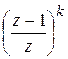 :
: 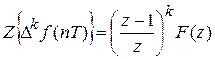 , где
, где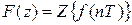 .
.
2. Изображение интеграла (конечной суммы) функции-оригинала
Свойства изменения изображений функции после ее интегрирования или взятия конечной суммы в дискретном варианте является “обратными” по отношению к свойствам дифференцирования или взятия конечных разностей:
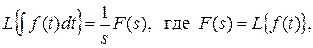
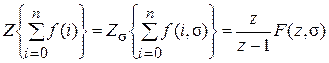
Резюмируя свойства 3 и 4 отметим, что s – оператор дифференцирования в непрерывной области; 1/ s – оператор интегрирования в непрерывной области; 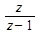 - оператор суммирования в дискретном времени;
- оператор суммирования в дискретном времени; 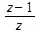 - оператор взятия конечной разности 1-го порядка.
- оператор взятия конечной разности 1-го порядка.
· Свойство изображения свертываемых функций (теорема свертки)
Сверткой двух непрерывных или дискретных функций называется функция, значения которой вычисляются согласно 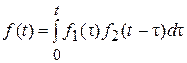 для непрерывного времени и
для непрерывного времени и 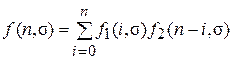 для дискретного времени.
для дискретного времени.
Формулировка свойства об изображении свертки одинакова для непрерывного и дискретного времени:
- изображение свертки равно произведению изображений свертываемых функций.
Если 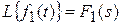 и
и 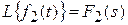 , то
, то
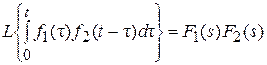 .
.
Если 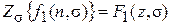 и
и 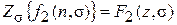 , то
, то
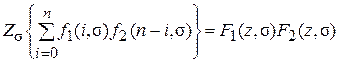 .
.
3. Определение начального значения функции оригинала по известному изображению
Зная изображение (F (s) в непрерывном случае и F (z) или F (z,s) в дискретном случае) можно сравнительно просто вычислить начальное и конечное значения функции-оригинала.
Начальное значение непрерывной функции
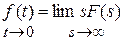 .
.
Начальное значение дискретной функции
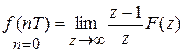 .
.
4. Конечное значение функции-оригинала
В непрерывном времени 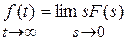 .
.
В дискретном времени 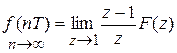 и при s ¹ 0
и при s ¹ 0
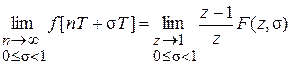 .
.
Рассмотрим еще несколько свойств, полезных для выполнения несложных преобразований.
5. Свойство изображения функции, умноженной на 
Для дискретного времени это свойство записывается следующим образом:
Если 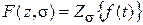 , то
, то 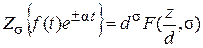 , где d =
, где d = 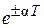 .
.
В частном случае s = 0 имеем
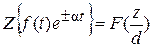 , где d =
, где d = 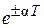 .
.
Записанное свойство позволяет без труда найти изображение экспоненциальной функции
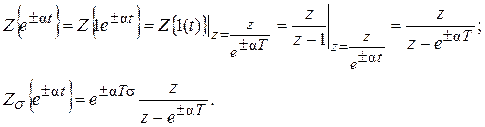
Для непрерывного времени в рамках этого свойства определяется изображение 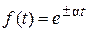
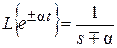 .
.
6. Свойство изображения функции, умноженной на tm ( m – целое число)
Это свойство имеет особое значение для дискретных систем, так как для непрерывных систем составлены подробнейшие таблицы соответствий функций и их изображений [6].
Для дискретных систем свойство формулируется отдельно для случаев s = 0 и s ¹ 0.
Для s = 0 имеем
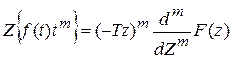 .
.
Словами: умножению функции-оригинала tm соответствует, с точностью до множителя, взятие m -производной в области изображений.
Пример. 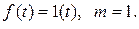
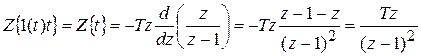 .
.
Для s ¹ 0 выражение изображения находится более сложно:
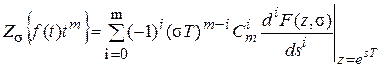 .
.
Здесь  - число сочетаний из m элементов по i.
- число сочетаний из m элементов по i.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 674; Нарушение авторских прав?; Мы поможем в написании вашей работы!