Элементами

Дискретная система с несколькими импульсными

W (z) = W ₁(z) W ₂(z), где W ₁(z) = Z { W ₁(s)}, W ₂(z) = Z { W ₂(s)}.

Правило: Передаточная функция нескольких последовательно соединенных непрерывных звеньев, разделенных импульсными элементами, равна произведению их Z -форм от непрерывных передаточных функций.

Дискретно-непрерывная система

W (z) = 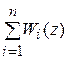, где W_i (z) = Z { W_i (s)}

Правило: Дискретная передаточная функция параллельного соединения непрерывных звеньев равна сумме дискретных передаточных функций отдельных ветвей.

Дискретная система с несколькими импульсными

элементами

Правило: Параллельные каналы с безинерционными звеньями и импульсными элементами, работающими синхронно и с одинаковым периодом квантования, могут быть заменены одним импульсным элементом, включенным после узла суммирования.

Дискретно-непрерывная система с единичной обратной связью

W _пнч(s)

X (s) E (s) Y (s)

Y (z,) = W (z,) E (z), где W (z,) = Z _s{ W _ПНЧ(s)}, E (z) = X (z) – Y (z). Подставляя в уравнение выхода, получаем

Y (z,) = W (z,) X (z) - W (z,) Y (z).

Положим =0, тогда

Y (z) = W (z) X (z) - W (z) Y (z) = .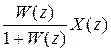

Подставляя в уравнение для Y (z,), получим

Y (z,) = W (z,)[ X (z) - Y (z)] = W (z,)[ X (z) - 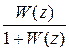X (z)] = 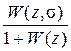X (z).

Передаточная функция замкнутой системы по управлению:

Ф_x (z,) = = .

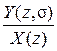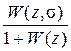Получим передаточную функцию замкнутой системы по ошибке:

Ф_е (z,)=,

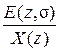где E (z,) = X (z,) - Y (z,). Подставляя в уравнение для ошибки Y (z,) =
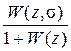= X (z), получим E (z,) = X (z,) - 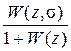X (z).

К сожалению, из полученного выражения E (z,) невозможно написать отношение E (z,) к X (z). Это можно сделать, только положив 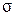=0, тогда
E (z) = X (z) - 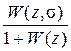X (z) = 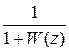X (z). Тогда передаточная функция замкнутой системы по ошибке при 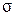=0 будет:

Ф_е (z) = = .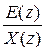

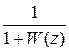Отметим, что по форме передаточные функции замкнутой дискретно-непрерывной системы полностью совпадают с соответствующими передаточными функциями непрерывной системы.

Дискретные системы произвольной структуры

Под произвольной структурой мы будем понимать расположение одного или нескольких импульсных элементов в различных местах дискретной системы, (в прямом канале, в канале обратной связи, между непрерывными звеньями и т.д.). Для записи уравнений или передаточных функций в таких системах следует использовать три основных правила записи уравнений в Z-изображениях.

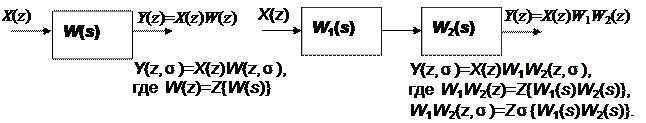*Правило1: Z-изображение выходного сигнала одного или нескольких последовательно соединенных непрерывных звеньев, подвергнутых воздействию дискретного сигнала, равно произведению Z-изображения, входного сигнала на Z-преобразование непрерывной передаточной функции. Рисунок ниже иллюстрирует это правило:

Правило2: Если одно или группа непрерывных последовательно соединенных звеньев подвергнута воздействию непрерывного сигнала, то Z-изображение выходного сигнала равно Z-преобразованию произведению изображения входного сигнала на непрерывные передаточные функции звеньев.

	W (s)		W 1(s)		W 2(s)

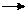
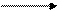X (s) Y (s) X (s) Y (s)

Y (z) = Z { X (s)} W (s)} = XW (z). Y (z) = Z { X (s)} W ₁(s) W ₂(s)} = XW ₁ W ₂(z)

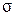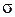Y (z,) = Z { X (s) W (s)} = XW (z,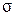) Y (z,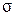) = Z { X (s)} W ₁(s) W ₂(s)} = XW ₁ W ₂(z,)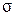

Правило 3. Z – изображение выходного сигнала группы звеньев, разделенных импульсными элементами, работающими синхронно и с одинаковым периодом квантования, равно произведению Z-форм передаточных функций отдельных звеньев.

Y (z) = X (z) W ₁(z) W ₂(z) W ₃(z), где W ₁(z) = Z { W ₁(s)}; W ₂(z) = Z { W ₂(s)}; W ₃(z) =
= Z { W ₃(s)};

Выражение Y (z,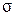) при 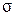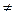0 довольно сложное и здесь не производится.

Пример: Простая система с одним импульсным элементом и неединичной обратной связью.

Для записи выражения передаточных функций системы по управлению G (s) и ошибке E (s) разорвем искусственно систему (разрыв всегда делается перед импульсным элементом или перед первым импульсным элементом, если их несколько).

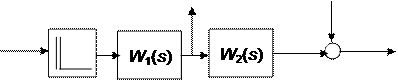Y (s) G (s)

E (s) E (s)

Запишем выражение для E (z)

E (z) = - E (z) W ₁ W ₂(z) + G (z) = G (z).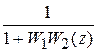

Передаточная функция замкнутой системы по управлению

Ф_g (z)== .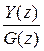

Передаточная функция замкнутой системы по ошибке:

Ф_e (z) = = .

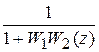Непосредственное применение правила Мэйсона к графу, эквивалентному структурной схеме дискретно-непрерывной системы, невозможно. Существует два пути использования правила Мэйсона для дискретно-непрерывных систем:

1) составление дискретного графа, в котором все переменные представлены дискретными величинами и для которого применение правила Мэйсона допустимо;

2) использования исходного эквивалентного графа с изменением формулы Мэйсона. Первый путь является более простым и эффективным и поэтому получил широкое распространение в практике анализа дискретно-непрерывных систем, особенно при решении задачи записи уравнений в Z-изображениях для систем сложной структуры с несколькими дискретными элементами.

В качестве иллюстрации использования формулы Мэйсона и записи уравнений в Z-изображениях рассмотрим простую дискретную систему с одним дискретным элементом и неединичной отрицательной обратной связью (рис. 2.23), использованную выше для составления эквивалентного графа.

Уравнения для входа и выхода в изображениях

E (s) = G (s) - W (s) W _ос(s) E *(s), Y (s) = W (s) E *(s).

Подвергнем Z-преобразованию записанные уравнения

E (z) = G (z) - WW _ос(z) E (z) = 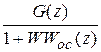, Y (z) = W (z) E (z) = G (z) .

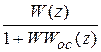Составляем дискретный граф системы

G (z) 1 E (z) W (z) y (z)

- WW _ос(z)

К такому графу правило Мэйсона применяется без всяких ограничений и условий:

= ; = .

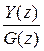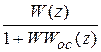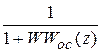Передачи между непрерывными и дискретными сигналами могут быть определены из так называемого составного графа.

Составным графом называется совокупность дискретного и эквивалентного графов, полученная путем соединения выходных узлов квантователей эквивалентного графа с аналогичными узлами дискретно графа дугами с единичными передачами.

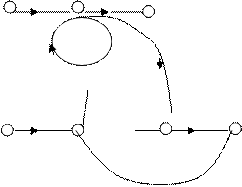G (z) 1 E (z) W (z) Y (z)

- WW _ос(z) 1

E (z) W ₁(s)

G (s) E (s) Y (s)

- W_x (s)

Составной граф для рассматриваемой нами системы будет следующим:

Применение правила Мэйсона к составному графу позволяет записать выражения передач для всех непрерывных и дискретных вершин. Так например,

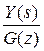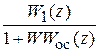=; E (s) = G (s) - 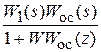G (z).

Дата добавления: 2014-10-31