Частотные характеристики

Полное переходное уравнение состояния

X (n) = A (n) X (0) + .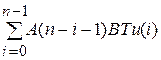

Переходной характеристикой полностью дискретной системы называется реакция дискретной системы на единичную дискретную ступенчатую функцию.

Графическое представление входного сигнала и математическое описание дискретной ступенчатой функции имеет вид:

g _и*(n) = 1, n 0; g _и*(n) = 0, n < 0.

Z – преобразование дискретного входного сигнала G _и(z) = .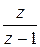

Z – преобразование переходной характеристики H (z) = D (z) G _и(z) = 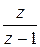D (z), где D (z) – дискретная передаточная функция дискретной системы. Таким образом, h (n) = Z ^-1{ D (z)}.

g *_и

0 1 2 3 4 5 6 n

Построение ЛАФЧХ дискретных систем и отдельных звеньев имеет свои характерные особенности. Они следуют из того факта, что выражения модуля и фазы КПФ дискретной системы являются функциями e^{j w T} и не логарифмируются непосредственно. Кроме того, диапазон частот дискретных характеристик
0 £ w £ p/ T не распространяется на всю ось абсцисс ЛАФЧХ непрерывных систем. Чтобы сделать выражения модуля и фазы логарифмируемыми и привести диапазон частот к подобному диапазону ЛАФЧХ непрерывных систем предварительно выполняется преобразование выражения ПФ дискретной системы с помощью подстановки 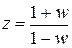. Эта подстановка называется w -преобразованием. Чтобы выяснить, как новая переменная w связана с обычной частотой w, используем связь z = e^{j w T}. Из формулы w -преобразования определяем

.

Используя формулу Эйлера e^{j a} = cosa + j sina, имеем

.

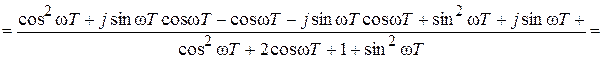
Окончательно имеем , где так называемая относительная псевдочастота. Нетрудно заметить, что при 0 £ w £ p/ T относительная псевдочастота будет меняться в диапазоне 0 £ 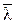£ ¥, т. е. Частотные характеристики дискретных систем, построенные в функции 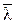, будут подобны характеристикам непрерывных систем. На практике частотные характеристики дискретных систем строятся в функции не относительной, а абсолютной псевдочастоты l = (2/ T)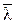. Дело в том, что при малых w (область низких частот) имеем

, а .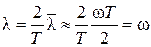

Это значит, что характеристики дискретных систем в области низких частот будут совпадать с характеристиками приведенной непрерывной части.

Посмотрим, как строятся ЛАФЧХ дискретных рассмотренных выше динамических звеньев: интегрирующего и апериодического 1-го порядка.

В ПФ дискретного интегратора 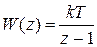вводим подстановку :

.

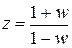Далее принимаем w = j (T /2)l и получаем

.

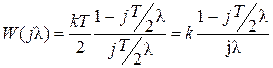Выражение ЛАЧХ

.

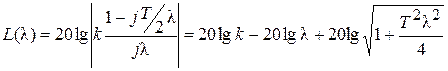Выражение ЛФЧХ

j(l) = - arctg(T /2)l - p/2.

Графики ЛАФЧХ интегрирующего звена показаны на рис. 5.10.

Из графиков видно, что в области низких частот ЛАФЧХ дискретного интегратора совпадают с ЛАФЧХ непрерывного интегрирующего звена (наклоном
–20 дБ/дек, фазовый сдвиг j = -p/2. Существенное отличие характеристик имеет место в области высоких частот (нулевой наклон и фазовый сдвиг j = - p).

Перейдем к апериодическому звену 1-го порядка. Эквивалентная схема дискретного апериодического звена имеет вид (рис. 5.11).

Дискретная передаточная функция апериодического звена

=

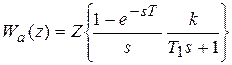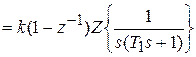. Для определения 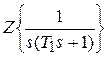предварительно разложим 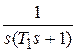на сумму простых слагаемых: = .

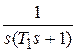Тогда 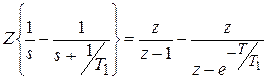. Подставляем в общую формулу W_a (z):

.

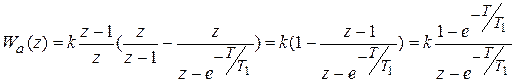Переходим к w -преобразованию W_a (z):

,

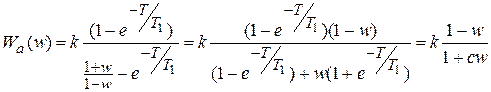где . Подставим w = j (T /2)l в выражение W_a (w):

.

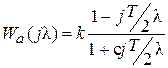Можно доказать, что . Поэтому .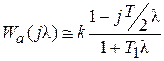

Переходя к ЛАФЧХ, получим

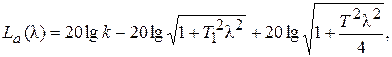
j_a(l) = - arctg(T /2)l - arctg T ₁l.

Графики L _а(l) и j_a(l) показаны на рис. 5.12.

Как и для интегрирующего звена, так и для апериодического звена 1-го порядка наблюдается совпадение ЛАФЧХ в области низких частот и существенное различие в области высоких частот для непрерывного и дискретного режимов работы.

Аналогично описанному выше строятся ЛАФЧХ других дискретных звеньев и систем. Свойство совпадения ЛАФЧХ в области низких частот сохраняет свою силу и для других более сложных звеньев и систем, что позволяет использовать для дискретных систем методы анализа и синтеза, разработанные для непрерывных систем.

Отметим, что для сложной передаточной функции непрерывной части дискретно-непрерывной системы построение ЛАФЧХ может быть выполнено приближенным способом, допускающим полное совпадение характеристик непрерывной и дискретной системы в области низких частот
0 £ l < 2/ T.

Дата добавления: 2014-10-31