Связь спектров непрерывного и дискретного сигналов

Для выяснения соотношения между Z -преобразованием и непрерывным преобразованием Лапласа, а также соотношения частотных свойств дискретного и непрерывного сигналов рассмотрим связь спектров этих сигналов.

Спектр непрерывного сигнала x (t) определяется его преобразованием Фурье 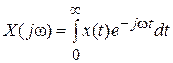, где w = 2p f – круговая частота сигнала, -¥ £ w £ ¥.

Чтобы найти выражение спектра дискретного сигнала, его надо предварительно представить в непрерывной форме с помощью d-функций

,

где U ^*(t) – последовательность d-функций, следующая с периодом T. Как периодическую функцию U ^*(t) можно разложить в ряд Фурье

,

где - круговая частота квантования, U_k – коэффициент ряда Фурье:

;

следовательно все коэффициенты ряда Фурье равны независимо от значения k. Для всей суммы d-функций

.

Подставляя U ^*(t) в выражение сигнала, получим

.

В таком виде сигнал x ^*(t) может быть подвергнут преобразованию Фурье:

где 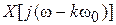- смещенный на k w₀ спектр непрерывного сигнала.

Общий вывод: спектр дискретного сигнала представляет бесконечную сумму (рис. 5.6) смещенных спектров непрерывного сигнала.

Это значит, что при определенной частоте квантования частотные характеристики дискретных систем будут представлять сумму смещенных частотных характеристик соответствующих непрерывных систем. Это также означает, что если максимальная частота спектра непрерывного сигнала (w_м) или, максимальная частота пропускания непрерывной части системы (w_п) меньше половины частоты квантования w₀, то наложение отдельных составляющих спектра не будет, и характеристики дискретной системы в существенном диапазоне частот будут совпадать с характеристиками непрерывной системы.

И так для системы необходимо .

Для неискаженной передачи непрерывного сигнала его дискретными значениями необходимо, чтобы максимальная частота спектра непрерывного сигнала .

Последнее условие является стержнем знаменитой импульсной теоремы Котельникова-Шеннона, согласно которой частота квантования w₀ =2p/ T должна быть по крайней мере в 2 раза больше максимальной частоты спектра непрерывного сигнала, передаваемого его дискретными значениями.

5.3.2. Связь между непрерывным преобразованием Лапласа
и Z-преобразованием

Из выражений непрерывных преобразований Лапласа и Фурье, приводимых ранее, следует, что и 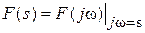. Используем эти соотношения для преобразований дискретных сигналов и получим . Если ввести замену , получим связь непрерывного преобразования Лапласа и Z -преобразования

.

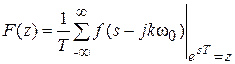Символически эту связь записывают следующим образом:

при s = 0 и ,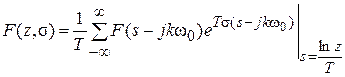

что символически означает .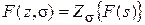

Записанные выражения связи F (z), F (z, s), F (s) имеют главным образом, теоретическое значение и не используются для практического определения F (z) и F (z, s) по F (s). Существует два способа практического перехода от F (s) к F (z) и F (z, s).

1 способ.

Предварительно определяется временная функция, соответствующая исходному изображению .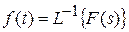

Чтобы облегчить переход в дискретную область, можно предварительно разложить F (s) на сумму простых слагаемых.

Пример. Пусть .

Разложение на простые слагаемые дает

.

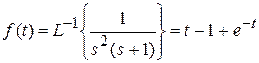Из таблиц соответствия имеем: . Таким образом . Подвергая f (t) Z -преобразованию, получим:

.

2 способ.

Осуществляется непосредственный переход от F (s) к F (z), используя таблицу соответствия изображений [6]. Если в таблице нет изображения, соответствующего заданному F (s), выполняют разложение F (s)на сумму более простых выражений.

Пример. Пусть 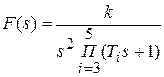. Представим заданное F (s) суммой слагаемых , где . Определим модифицированное Z -преобразование

Частный случай, важный в практике записи Z -изображений по заданному F (s).

Если , то .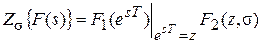

Пример. Пусть .

.

.

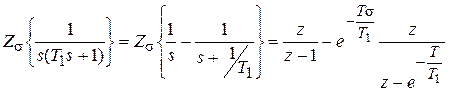Окончательно

.

Дата добавления: 2014-10-31