Поняття про процесовий ансамбль частинок

Будь-який процес можна подати послідовністю перетворень (розриву, сполучення, рекомбінації тощо) зв’язків під впливом якихось сил. У реальних процесах із участю великих кількостей речовин, у будь-якій частині об’єму реактора щосекунди видозмінюються міріади зв’язків між такого ж порядку кількістю частинок. У таких умовах простежувати поведінку кожної частинки, а тим більше керувати нею є справою безнадійною.

На щастя поведінка частинок-учасниць процесу не є довільною, а є обмеженою взаємодією між ними. Тому, як і у великому оркестрі, де кожна група музичних інструментів, підпорядковуючись єдиному зв’язуючому їх керуванню, виконує частину музичної фрази, так і кожна група частинок, відмінних за природою, складом, енерґією, стереометрією, виконує свою частину окремої хімічної дії. Така множина частинок, об’єднаних єдиною самоузгодженою чи керованою дією – процесом, і називається процесовим ансамблем.

У підсумку процесу всередині ансамблю перерозподіляється енерґія, змінюється імпульс частинок, змінюються їхні маґнітні та електричні характеристики. Однак із курсу фізики відомо, що середньостатистичною мірою енерґії частинок ансамблю є температура T [K] ансамблю; його об’єм V [м³] відображує середньостатистичне співвідношення кінетичної та потенціальної енерґії; тиск р [Па] відповідає середнім значенням імпульсу; напруженості електричного Е [B/м] та маґнітного Н [A/м] полів визначають середньостатистичні електричні й маґнітні характеристики частинок, концентрація С_і [мас. %; моль/л; моль/кг; мольн.%] відображує кількісне співвідношення частинок різного типу. Безпосередньо вимірювані величини, такі як Т, р, V, С_і , Н, Е, тощо, які середньостатистично відображують якусь із якостей частинок, що складають ансамбль, називаються параметрами. Набір числових значень параметрів визначає стан ансамблю. Оскільки параметри будь-якого ансамблю пов’язані рівнянням стану, то частина параметрів виявляється залежною, тобто визначається з рівняння стану, за умови, що інші параметри – незалежні – задано чи визначено дослідним шляхом. Очевидно, що контролюючи та керуючи змінами параметрів, ми встановлюємо чи спрямовано змінюємо стан ансамблю й, таким чином, контролюємо чи скеровуємо середньостатистичний перебіг процесу. При цьому, щоб задати стан ансамблю нам необхідно задати (чи знати) рівняння стану та числові значення незалежних параметрів. Щоб довільно змінювати стан необхідно змінити хоча б один із параметрів. Для спрямованої зміни стану необхідно змінити значення незалежних параметрів.

Хімічна термодинаміка вивчає взаємоперетворення різних форм енерґії та її обмін між системою та зовнішнім середовищем, а також енерґетичні ефекти, що супроводжують хімічні та фазові процеси, можливість і напрямок їх самочинного перебігу. Вона розглядає лише початковий та кінцевий стани, не враховуючи шлях перебігу процесу та його розвиток у часі. Хімічна термодинаміка неначе ділить світ на дві частини – систему та зовнішнє середовище.

Функція стану – це така властивість системи, зміну якої можна обчислити, беручи до уваги лише початковий та кінцевий стани системи, не враховуючи механізму процесу. До функцій стану належить повна енерґія Е, що складається з енерґії кінетичної Е_k, енерґії потенціальної Е_р та внутрішньої енерґії U; ентальпія (тепловміст) H; ентропія (міра безладу) S; енерґія Ґіббса(дієздат-ність, роботоздатність) G, тощо. Зміна функцій стану дає уявлення про енерґетику процесів.

Розділ хімічної термодинаміки, що вивчає енерґетичні ефекти реакцій, називають термохімією. У термохімії розрізняють два типи хімічних реакцій: екзотермічні (тепловміст системи зменшується) ендотермічні (тепловміст системи збільшується).

Речовини містять енерґію у прихованому вигляді, запас якої залежить від кількості, складу та стану речовини. Вона вивільняється під час хімічних і деяких фізичних процесів і називається внутрішньою енерґією. Внутрішня енерґія – це усі види енерґії руху та взаємодії частинок системи, крім кінетичної та потенціальної енерґії системи загалом. Для термодинамічного аналізу важливе не саме значення енерґії (абсолютну величину якої встановити неможливо), а її зміна за зміною стану та умов існування системи, ΔU.

Кількісною мірою зміни внутрішньої хімічного процесу є тепловий ефект реакції Q – кількість енерґії, що виділяється або поглинається системою у процесі необоротної хімічної реакції (за умов сталості об'єму, тиску чи температури протягом процесу). Хімічні реакції звичайно відбуваються при сталому тиску (у відкритій посудині) або за сталого об’єму (в автоклаві), тобто є ізобарними або ізохорними процесами. У першому випадку (p = const) тепловий ефект реакції складатиметься зі зміни внутрішньої енерґії (ΔU) та виконання системою роботи (pΔV) таким чином Q = ΔU + pΔV = ΔН, отже тепловий ефект реакції дорівнює зміні ентальпії системи. У другому випадку (V = const) уся теплота йде на зміну внутрішньої енерґії системи (ΔU), таким чином Q = ΔU.

5.2. Перший закон термодинаміки

Зовнішній енерґетичний вплив на систему порушує рівноважні чи динамічні умови, що склалися у ній, змінює енерґію системи, яка частково перетворюється у роботу. Таке міркування дозволило Ю.Р.Майєрові сформулювати закон, який є у сутності законом збереження енерґії: “Енерґія, що підводиться до системи, витрачається на зміну внутрішньої енерґії системи та на здійснення нею зовнішньої роботи.”

Якщо записати вираз математично одержимо тепловий ефект реакції в ізобарній системі: ΔН = ΔU + pΔV (5.1)

Як і значення внутрішньої енерґії абсолютну величину ентальпії встановити неможливо (бо невідомі її значення за абсолютного нуля), визначають лише зміни цих величин за теплоємністю:

ΔН = υС_pΔТ та ΔU = υС_VΔТ (5.2)

де υ – кількість речовини (моль), С_p та С_V – молярні теплоємності за сталих тиску та об’єму.

Оскільки внутрішня енерґія та ентальпія є функціями стану не має значення як змінюються параметри системи протягом процесу, а має значення тотожність цих параметрів щодо початкових.

Для порівняння теплових ефектів різних процесів термохімічні розрахунки роблять відносно одного моля речовини за стандартних умов – температури 298 К (25 ^оС) та тиску 101325 Па (1 атмосфера).

Стандартна ентальпія утворення складної речовини – зміна ентальпії у процесі утворення одного моля її з простих речовин у найбільш термодинамічно стійкому стані за стандартних умов. Оскільки значення ентальпії залежить не лише від температури, а й від аґреґатного стану речовини, то у термохімічних рівняннях зазначають аґреґатний стан речовини. Наприклад:

Н₂(г) + 1/2O₂(г) = Н₂О(р); ΔН = – 286 кДж/моль;

Н₂(г) + 1/2O₂(г) = Н₂О(г); ΔН = – 242 кДж/моль.

Перехід енерґії зі системи у зовнішнє середовище супроводжується зменшенням тепловмісту. Цим можна пояснити, що зміна ентальпії для екзотермічних процесів є від’ємною, відповідно для ендотермічних процесів – додатною. (Аналогічними будуть знаки зміни внутрішньої енерґії для ізохорних процесів).

5.3. Закони термохімії

Ще одним проявом закону збереження енерґії є закони термохімії:

1. Закон Лавуазьє-Лапласа (1780): Зміна ентальпії прямої реакції за абсолютною величиною дорівнює ентальпії зворотної реакції та протилежна за знаком. ΔН_пр. = – ΔН_зв.. Тобто, чим більше теплоти виділяється у певній реакції, тим більше теплоти поглинатиметься при проведенні зворотної до неї реакції, а також і у випадку з протилежним тепловим ефектом.

2. Закон Ґесса (1840): Зміна ентальпії реакції залежить лише від початкового та кінцевого стану реаґентів, але не залежить від шляху перебігу процесу (тобто від числа і характеру проміжних стадій).

Наприклад водний розчин хлориду амонію можна одержати двома шляхами: І) NH₃ + H₂O Û NH_3,aq, Q₁; HCl + H₂O Û HCl_aq, Q₂;

NH_3,aq + HCl_aq, Û NH₄Cl_aq, Q₃.

ІІ) NH₃(г) + HCl(г) Û NH₄Cl(г), Q₄; NH₄Cl(г) + H₂O Û NH₄Cl_aq, Q₅.

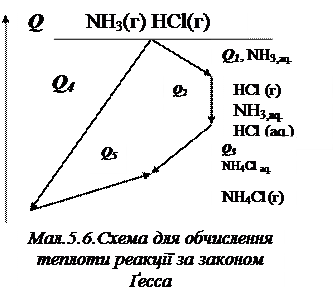У наведених реакціях “aq” означає водний розчин даної речовини, Q_i – відповідне значення теплового ефекту.

Для наведених процесів властива схема, подана на малюнку 5.6. Зі схеми випли-ває, що, оскільки початковий та кінцевий стани однакові, то справедливо:

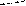
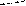Q₁ + Q₂ + Q₃ = Q₄ + Q₅.

Перед тим, як зробити висновок із закону Ґесса введемо наступні визначення:

1. Енерґія, яка виділяється при утворенні 1 моля даної речовини з вихідних прос-тих речовин, називається енерґією утворення даної речовини.

Із закону Ґесса випливають два важливі наслідки:

1. Ентальпія утворення речовин не залежить від способу одержання сполуки.

2. Зміна ентальпії реакції дорівнює різниці суми змін ентальпій утворення продуктів реакції та суми змін ентальпій вихідних речовин (з урахуванням стехіометричних коефіцієнтів).

ΔН (хім. р-ції) = Σ ΔН (прод. р-ції) – Σ ΔН (вих. речовин) (5.3)

5.4. Поняття про ентропію

Як відомо, кожна система намагається перейти до стану з найменшим запасом енерґії. Тому самочинний (мимовільний) перебіг будь-якої реакції супроводжується зменшенням внутрішньої енерґії. Згідно принципом максимальної роботи Томсена – Бертло (1867) мірою хімічної спорідненості є тепловий ефект реакції: реакція самочинно відбувається лише тоді, коли вона супроводжується виділенням теплоти (тобто є екзотермічною). Однак хімічна форма руху матерії є складнішою за механічну, тому ще одним чинником спрямованості процесу є тенденція до переходу до найбільш імовірного стану (тобто стану з найбільшою невпорядкованістю). Функцією стану, яка визначає невпорядкованість є ентропія: S = k · lnW (5.4),

де k – константа Больцмана, W – термодинамічна ймовірність.

Для молярної ентропії S = R · lnW (5.5),

R – універсальна газова стала: k = R/N_A

Функція від імовірності може бути лише логарифмічною, бо ймовірності на відміну від енерґій не додаються, а перемножуються. Загальна ентропія кількох складових системи є сумою ентропій цих складових S_Σ = Σ S_і, а загальна ймовірність дорівнює добутку їхніх імовірностей W_Σ = Π W_і.

5.5. Другий закон термодинаміки

Другий закон був уперше сформульований Р. Клаузіусом у 1854 році, однак і досі не стихають суперечки щодо його сутності. Сутність же зводиться до того, що закон пояснює, у якому напрямку перепливає енерґія та що при цьому з нею відбувається.

На сьогодні відомо близько 80 формулювань другого закону, однак, якщо формулювань багато, то жодне з них не є повним і не здатне відобразити всю багатоманітність розглядуваних явищ. За таких обставин можна подати ориґінальне визначення, що синтезує узагальнюючу сутність вищезазначених визначень: “Будь-який тип енерґії, самочинно (спонтанно) поширюючись від більшого значення свого потенціалу до меншого частково витрачається на виконання роботи, а частково розсіюється у вигляді тепла”.

5.6.Третій закон термодинаміки

Перехід системи із більш упорядкованого стану у менш упорядкований супроводжується збільшенням ентропії. Але якщо температура прямує до нуля ентропія речовин у стані ідеальних кристалів також прямує до нуля.

У цьому суть третього закону термодинаміки (Нернст, 1906). Виходячи з цього, на відміну від ентальпії та внутрішньої енерґії, можна обчислити абсолютні значення ентропії за різних температур.

Проте для різного роду перетворень важливо знати не абсолютне значення ентропії, а її зміну, якай характеризує можливість перебігу процесу та так само, як і енерґетичні функції стану підпорядкована наслідкові зі закону Ґесса:

ΔS (хім. р-ції) = Σ S (прод. р-ції) – Σ S (вих. речовин) (5.6)

При цьому слід мати на увазі, що для простих речовин ентропію не приймають рівною нулеві Для термодинамічно оборотних процесів зміна ентропії пов’язана з поглинутою теплотою рівнянням:

ΔS = Q/T (5.7)

За допомогою цього рівняння можна визначити зміну ентропії, зокрема при фазових переходах. Щоб значення ентропії можна було порівнювати, їх також відносять до стандартних умов (S^о₂₉₈).

Ентальпія відображає виграш в енерґії внаслідок зміни хімічних зв’язків, тобто фактично є енерґією сполучення. Ентропія – навпаки – відображає енерґію роз’єднання (дезорґанізації). Оскільки ентропія е похідною від енерґії за температурою, то умовою рівноваги є рівність цих енерґій, а саме:

ΔН = TΔS.

5.7. Вільна енергія Ґіббса

Самочинно відбуваються процеси, які перебігають зі зменшенням потенційної енерґії. Тому, якщо немає рівноваги, напрямок перебігу процесу визначатиме величина потенційної енерґії (за сталих тиску та температури), яка й становить різницю зміни ентальпії та добутку абсолютної температури й зміни ентропії, яку називають зміною ізобарно-ізотермічного потенціалу або зміною вільної енерґії Ґіббса (на честь Дж. Ґіббса, який увів це поняття у термодинаміку у 1874 році): ΔG = ΔН – TΔS (5.8).

А саме рівняння 5.8 також було названа на честь цього вченого рівнянням Ґіббса. Енерґія Ґіббса визначає здатність системи виконувати зовнішню роботу, а саме: – ΔG = А_max..

Загалом термодинамічною умовою можливості самочинного перебігу процесу є від’ємне значення зміни вільної енерґії Ґіббса (ΔG_р,Т < 0), тобто реакції самочинно відбуваються лише зі зменшенням потенціалу Ґіббса.

За низьких температур ΔН >> TΔS, тому у визначенні можливості та напрямку процесу вирішальне значення має ентальпійний чинник, що можна виразити як ΔG ≈ ΔН.

За дуже високих температур TΔS >> ΔН. Тоді, навпаки, вирішальним стає ентропійний чинник і ΔG ≈ – TΔS. Проте у будь-якому разі зміна енерґії Ґіббса у певному процесі так само як і зміна ентальпії чи зміна ентропії не залежить від шляху перебігу процесу, а отже є підпорядкованою наслідкові з закону Ґесса: ΔG (хім. р-ції) = Σ ΔG (прод. р-ції) – Σ ΔG (вих. речовин) (5.9).

Так само як і для змін ентальпій утворення і для ентропій індивідуальних речовин існують стандартні зміни енерґій Ґіббса занесені у таблиці термодинамічних констант. За допомогою цих величин можна визначити можливість і напрямок того чи іншого процесу за стандартних умов.

Питання для самоперевірки

1. Що таке тепловий ефект реакції? У яких одиницях його вимірюють?

2. Які реакції називаються екзотермічними, а які ендотермічними? Яке значення має ΔН для цих процесів?

3. Як формулюється закон Ґесса та які наслідки з нього випливають?

4. Що таке стандартна теплота утворення хімічної сполуки?

5. Що називається внутрішньою енерґією системи?

6. Що таке ентропія? Як вона залежить від агрегатного стану речовини та температури?

7. Що таке енерґія Ґіббса? Як пов’язана зміна енерґії Ґіббса з термодинамічною можливістю перебігу процесу?

8. Якими рівняннями пов’язані між собою величини ΔG, ΔН і ΔS?

КОНТРОЛЬНІ ЗАВДАННЯ

1. Обчисліть DН⁰₂₉₈ хімічної реакції при спалюванні 38 г сірковуглецю: CS₂(р) + 3O₂(г) = CO₂(г) + 2SO₂(г).

Відповідь: – 537,56 кДж.

2. Обчисліть DН⁰_298,утв. пероксиду водню за термохімічним рівнянням: H₂O₂(р) = H₂O(р) + 1/2O₂(г); DН⁰_{298, х.р.} = – 98,5 кДж.

Відповідь: – 187,34 кДж / моль.

3. Обчисліть DН⁰₂₉₈ хімічної реакції:

Fe₂O₃(к) + 3CO(г) = 2Fe(к) + 3CO₂(г).

Зробіть висновок про тип даної термохімічної реакції.

Відповідь: +10,96 кДж.

4. Обчисліть DН⁰₂₉₈ хімічної реакції та зробіть висновок про тип даної термохімічної реакції: 2Mg(к) + CO₂(г) = 2Mg(к) + C(к).

Відповідь: – 808,98 кДж.

5. Обчисліть DН⁰₂₉₈ хімічної реакції і зробіть висновок про тип даної термохімічної реакції: SiО₂(к) + 2Mg(к) = 2MgО(к) + Si(к).

Відповідь: – 343,18 кДж.

6. Обчисліть DН⁰_298,утв. пропану, якщо відомо, що при згорянні 11 г пропану в кисні з одержанням рідкої води виділяється 559,8 кДж теплоти.

Відповідь: – 84,68 кДж / моль.

7. Обчисліть DН⁰₂₉₈ згоряння 10 л етилену за нормальних умов з утворенням рідкої води.

Відповідь: – 629,9 кДж.

8. За термохімічними рівняннями реакцій:

KClО₃(к) = KCl(к) + 3/2O₂(г), DН⁰_{298, х.р.} = – 44,65 кДж;

KClО₄(к) = KCl(к) + 2O₂(г), DН⁰_{298, х.р.} = – 2,39 кДж;

обчисліть DН⁰₂₉₈ хімічної реакції: 4KClО₃(к) = 3KClО₄(к) + KCl(к).

Відповідь: – 171,38 кДж.

9. Обчисліть DН⁰_{298,розкл.} аміаку за термохімічним рівнянням:

2NH₃(г) + 3/2O₂(г) = N₂(г) + 3H₂O(р); DН⁰_{298, х.р.} = – 776 кДж.

Відповідь: +45,76 кДж / моль.

10. При взаємодії 2,1 г заліза з надлишком сірки виділилося 3,77 кДж теплоти. Складіть термохімічне рівняння цього процесу. Обчисліть DН⁰₂₉₈ (утв.) FeS.

Відповідь: – 100,53 кДж / моль.

11. Обчисліть DН⁰_298,утв. PH₃ за термохімічним рівнянням реакції:

2PH₃(г) + 4O₂(г), = P₂O₅(к) + 3H₂O(р); DН⁰_{298, х.р.} = – 3851,52 кДж.

Відповідь: +5,0 кДж / моль.

12. Обчисліть DН⁰_{298,розкл.} 31 г Ca₃(PO₄)₂ за термохімічним рівнянням реакції: 3CaО(к) + P₂O₅(к) = Ca₃(PO₄)₂(к); DН⁰_{298, х.р.} = – 739 кДж.

Відповідь: +73,9 кДж.

13. Визначте DН⁰₂₉₈ утворення CuО (к), якщо при відновленні 12,7 г CuО (к) вугіллям з одержанням чадного газу (СО) поглинається 7,25 кДж теплоти.

Відповідь: – 156,2 кДж / моль.

14. Складіть термохімічне рівняння реакції утворення NO з азоту та кисню, якщо при цьому поглинається 90,37 кДж теплоти.

15. Обчисліть DН⁰₂₉₈ хімічної реакції Зазначте тип даної термохімічної реакції: SO₂(г) + 2H₂O(г) + Br₂(г) = H₂SO₄(р) + 2HBr(г).

Відповідь: – 45,36 кДж.

16. Обчисліть DН⁰₂₉₈ розкладу 1 кг натрій хлориду.

Відповідь: 7023,9 кДж.

17. Обчисліть DН⁰₂₉₈ хімічної реакції:

Na₂CO₃(к) + SiО₂(к) = Na₂SiО₃(к) + CO₂(г).

Зазначте тип даної термохімічної реакції.

Відповідь: 76,8 кДж.

18. Складіть термохімічне рівняння реакції взаємодії Nа(к) з Н₂O(р), якщо при цьому виділяється 283,7 кДж теплоти.

19. Визначте DН⁰₂₉₈ утворення H₂S за термохімічним рівнянням реакції:

H₂S(г) + 3/2O₂(г) = H₂O(г) + SО₂(г); DН⁰_{298, х.р.} = – 518,59 кДж.

Відповідь: 20,15 кДж / моль.

20. Обчисліть DН⁰₂₉₈ розкладу 16 г сірчаної кислоти.

Відповідь: 132,46 кДж.

21. Обчисліть значення величин DН⁰_298, DG^о_298, DS^о_298, для реакції: C₂H₄(г)+H₂O(р) = C₂H₅OH(р). Зробіть висновок про можливість мимовільного перебігу даної реакції при 298 К.

Відповідь: 133,09 кДж; 171,34 кДж; – 128,36 Дж / К.

22. Без обчислень визначте знак DS^о наступних реакцій:

а) AB(к) + B₂(г) = AB₃(к); в) 4HCl(г) + O₂(г) = 2Cl₂(г) + 2H₂O(г);

б) NO₂(г) = NO₂(к); г) CaCO₃(к) = Ca(к) + CO₂(г).

23. Обчисліть DG^о₂₉₈ хімічної реакції: CaSO₄(к) + 4C(граф.) = Ca(к) + 4CO(г),

використовуючи значення DН⁰₂₉₈ і DS^о₂₉₈ для даної реакції.

Відповідь: 287,13 кДж.

24. Визначте можливість мимовільного перебігу реакції при 373 К:

TiО₂(к) + 2C(граф.) = Ti(к) + 2CO(г).

Відповідь: не можлива.

25. Визначте за DG^о_298,х.р. можливість самочинного перебігу р-ції при 500 К: Fe₂O₃(к) + 3H₂(г) = 2Fe(к) + 3H₂O(г).

Відповідь: не можлива.

26. Визначте температуру (Т, К), за якої настане рівновага у системі:

С₂Н₆(г) + 2СО₂(г) = 4СО(г) + 3H₂(г).

Відповідь: 819,5 К.

27. Визначте, за якої температури (Т, К), настане рівновага в системі:

N₂(г) + 3H₂(г) = 2NН₃(г).

Відповідь: 465,86 К.

28. Виходячи зі значень DН⁰₂₉₈ і DS⁰₂₉₈ хімічної реакції NН₃(г) + HСl(г) = =NН₄Cl(к), обчисліть DG⁰_298,х.р.. Чи може ця реакція перебігати за стандартних умов?

Відповідь: – 92,1 кДж.

29. Поясніть, у якому випадку реакція термодинамічно неможлива за будь-якої температури: а) DН⁰ < 0, DS⁰ < 0; б) DН⁰ < 0, DS⁰ > 0; в) DН⁰ > 0, DS⁰ < 0.

30. Які з перерахованих оксидів можуть бути відновлені дією металевого алюмінію при 298 К: CaО, FeО, CuО, PbО, Fe₂O₃, Cr₂O₃ ?

31. У якому з наступних випадків реакція термодинамічно можлива за будь-якої температури: а) DН⁰ < 0, DS⁰< 0; б) DН⁰ > 0, DS⁰ > 0; в) DН⁰ < 0, DS⁰> 0.

32. Зазначте, які з перелічених оксидів – CaО, ZnО, SnО₂, NiО, Al₂O₃ – можна відновити воднем до вільного металу при 298 К.

33. Поясніть, чому за високих температур (Т > 1200 К) критерієм, що визначає мимовільний перебіг реакцій є DS⁰ хімічної реакції.

34. Обчисліть DG^о₂₉₈ хімічних реакцій:

Cu(к) + ZnО(к) = CuО(к) + +Zn(к);

N₂(г) + 2O₂(г) = 2NO₂(г);

та поясніть, чому їхній перебіг термодинамічно неможливий за стандартних умов.

Відповідь: 191,0 кДж; 103,68 кДж.

35. Визначте, при якій температурі (Т, К) можливий мимовільний перебіг реакції: СаСО₃(к) = СаО(к) + 2СО₂(г).

Залежністю DН⁰₂₉₈ і DS⁰₂₉₈ від температури знехтувати.

Відповідь: 1106,6 К.

36. Обчисліть значення DG^о₂₉₈ хімічних реакцій:

FeО(к) + 1/2C(граф.) = Fe(к) + 1/2CO₂(г),

FeО(к) + C(граф.) = Fe(к) + CO(г),

FeО(к) + CO(г) = Fe(к) + CO₂(г).

Зазначте, яка з даних реакцій перебігає за стандартних умов.

Відповідь: 46,45 кДж; 107,08 кДж; – 12,76 кДж.

37. Обчисліть DS^о₂₉₈ і DG^о₂₉₈ реакції:

C₂Н₄(г) + 3O₂(г) = 2CO₂(г) + 2Н₂О(г);

Чи можливий її мимовільний перебіг за стандартних умов.

Відповідь: – 31,01 Дж / К; – 1314,08 кДж.

38. Обчисліть DS^о₂₉₈ і DG^о₂₉₈ реакції: 4NН₃(г) + 5O₂(г) = 4NO(г) + 6Н₂О(p),

та визначте можливість її мимовільного перебігу при 298 К.

Відповідь: – 533,5 Дж / К; – 1012,28 кДж.

39. Не здійснюючи обчислень, визначте знак DS⁰ наступних реакцій:

а) СО₂(к) = СО₂(г); б) 2CH₃OH(г) + 3O₂(г) = 4H₂O(г) + 2CO₂(г);

в) 2NH₃(г) = N₂(г) + 3H₂(г); г) 2H₂S(г) + 3O₂(г) = 2H₂O(г) + 2SO₂(г).

40. Обчисліть значення DG^о₂₉₈ наступних процесів: 2NO(г) + O₂(г) = 2NO₂(г);

NiО(к) + Pb(к) = Ni(к) + PbО(к); Pb(к) + CuО(к) = Cu(к) + PbО(к).

У якому напрямку кожний з них перебігає мимовільно (ст. у.).

Відповідь: – 69,7 кДж; 23,51 кДж; – 61,3 кДж.

Приклади розв’язання задач

Приклад 1. Складіть термохімічне рівняння реакції горіння 1 моль ацетилену, якщо при цьому виділяється 1255,61 кДж теплоти.

Розв’язання. Рівняння хімічної реакції горіння ацетилену має вигляд: 2С₂Н₂ + 5О₂ = 4CO₂ + 2Н₂О. У термохімічному рівнянні слід зазначити агрегатний стан кожної речовини (газоподібний – (г), рідкий – (р), твердий – (т), кристалічний – (к)) та зміну ентальпії (DН) у процесі реакції. Ентальпія утворення (DН⁰ _утв.) даної сполуки – це тепловий ефект реакції одержання 1 моль цієї сполуки з простих речовин, узятих у їхньому найбільш стійкому стані за даних умов. Звичайно DН⁰ _утв. відносять до стандартних умов: Т = 298К и р = 101,32 кПа, і позначають DН⁰ ₂₉₈. Якщо DН⁰ _298,х.р.> 0, то реакція ендотермічна і супроводжується поглинанням тепла, якщо DН⁰ _298,х.р.< 0, то реакція є екзотермічною та супроводжується виділенням теплоти. Скористаємось даними задачі й одержимо: С₂Н₂(г) + 2,5О₂(г) = 2CO₂(г) + Н₂О(г); DН⁰ _298,х.р. = – 1255,61 кДж,

що означає те, що реакція є екзотермічною.

Приклад 2. Обчислити ентальпію утворення CS₂ за стандартних умов з рівняння: CS₂(р) + 3О₂(г) = CO₂(г) + 2SО₂(г). DН⁰ _х.р. = – 1075 кДж,

DН⁰ (CO₂) = – 393,5 кДж/моль, DН⁰ (SО₂) = – 296,9 кДж/моль.

Розв’язання. За наслідком із закону Ґесса тепловий ефект реакції (DН⁰_х.р.) дорівнює сумі теплот утворення продуктів реакції, зменшеній на суму теплот утворення вихідних речовин з урахуванням коефіцієнтів перед формулами цих речовин у рівнянні реакції:

DН⁰ _х.р. = SDН⁰ _прод. – SDН⁰ _{вих.реч.}

У даному випадку: DН⁰ _298,х.р. = (DН⁰ ₂₉₈(CO₂) + 2 DН⁰ ₂₉₈(SО₂)) – (DН⁰ ₂₉₈(CS₂) + 3 DН⁰ ₂₉₈(O₂)); оскільки DН⁰ ₂₉₈ простих речовин дорівнюють 0, то DН ⁰_298,х.р. = =(DН⁰ ₂₉₈(CO₂) + 2 DН⁰ ₂₉₈(SО₂)) – DН⁰ ₂₉₈(CS₂).

Звідси DН⁰ ₂₉₈(CS₂)=(DН⁰ ₂₉₈(CO₂) + 2 DН⁰ ₂₉₈(SО₂)) – DН⁰ _298,х.р. = –393,5 кДж/моль+ + 2 × (–296,9 кДж/моль) – (–1075 кДж) = 87,8 кДж/моль.

Приклад 3. Не здійснюючи обчислень, поясніть, як змінюється ентропія системи (DS): а) при переході води в пару; б) у реакції:

N₂(г) + 3H₂(г) = 2NH₃(г).

Відповідь. Ентропія (S) є мірою невпорядкованості стану речовини і характеризує ймовірність даного мікростану (W) даної макросистеми: S = k × lnW, де стала Больцмана k = 1,38 × 10^-23 Дж/К.

Ентропія залежить від температури, тиску, об’єму і маси системи. S_газу > >S_рідк. > S_ам.тв. > S_крист., оскільки при переходах кристал ® рідина і рідина ® газ (пара) взаємодія між частинками слабшає, і невпорядкованість у системі зростає. У даному випадку при переході води в пару об’єм системи збільшується, можливість хаотичного руху молекул різко зростає, отже, ентропія системи збільшується. Якісно про зміну ентропії судять зі зміни об’єму: якщо зміна об’єму (DV) більше нуля, то й DS > 0, якщо DV < 0, те і DS < 0, якщо DV = 0, то і DS ≈ 0.

У системі N₂(г) + 3H₂(г) = 2NH₃(г) до реакції 1 + 3 = 4 об’єми газоподібних речовин, а після реакції 2 об’єми, тобто, у процесі реакції об’єм системи зменшується, отже, й ентропія системи теж зменшується (DS < 0).

Приклад 4. Обчисліть зміну енерґії Ґіббса у хімічній реакції

4NH₃(г) + 5O₂(г) = 6H₂O(г) + 4NО(г)

і зробіть висновки про можливість мимовільного перебігу даної реакції за стандартних умов.

Розв’язання. Енерґія Ґіббса (G) – термодинамічна функція стану системи, тому зміну енерґії Ґіббса (DG_х.р.) можна розрахувати за наслідком із закону Ґесса за стандартних умов DG⁰_х.р. = SDG⁰_прод. – SDG⁰_{вих.реч.},

де DG⁰_прод. – зміни енерґій Ґіббса продуктів реакції, DG⁰_{вих.реч.} – зміни енерґій Ґіббса вихідних речовин.

Стандартні зміни енерґій Ґіббса простих речовин прийнято вважати рівними нулю. Для даної системи:

DG⁰_298,х.р. = (6 DG⁰₂₉₈ (Н₂О) + 4 DG⁰₂₉₈ (NО)) – (4 DG⁰₂₉₈ (NH₃) + 5 DG⁰₂₉₈ (О₂));

оскільки DG⁰₂₉₈ (О₂) = 0,

то DG⁰_298,х.р. = (6 DG⁰₂₉₈ (Н₂О) + 4 DG⁰₂₉₈ (NО)) – 4 DG⁰₂₉₈ (NH₃).

Взявши в таблиці 1 потрібні дані DG⁰₂₉₈, знаходимо:

DG⁰_298,х.р. = 6 × (–228,8) + 4 × (86,89) – 4 × (–16,64) = –959,48 кДж.

Величина DG_х.р. є мірою хімічної спорідненості реагуючих речовин. Мимовільно перебігають хімічні процеси, для яких зміна енерґії Ґіббса менше нуля. Якщо DG_х.р. > 0, процес за даних умов термодинамічно неможливий, а якщо DG_х.р = 0, то система знаходиться у термодинамічній рівновазі. У даному випадку DG⁰_298,х.р. < 0, отже, цей процес термодинамічно можливий за стандартних умов.

Приклад 5. Обчисліть, за якої температури пряма та зворотна реакції в системі стануть рівноймовірними: Н₂(г) + І₂(к) = 2HІ(г).

Розв’язання. За рівнянням Ґіббса: DG = DН – ТDS, де DН – зміна ентальпії у процесі реакції; DS – зміна ентропії в процесі реакції; Т – абсолютна температура, К. Якщо система знаходиться в стані рівноваги, то DG = 0, тоді

DН = ТDS; Т = DН/DS.

Використовуємо табличні дані для обчислення DН_х.р. і DS_х.р. за наслідком із закону Ґесса: DН_х.р. = 2 DН⁰₂₉₈ (HІ) = 2 × 26,55 = 53,1 кДж.

DS_х.р. = 2 S⁰₂₉₈ (HІ) – (S⁰₂₉₈ (H₂) + S⁰₂₉₈ (І₂(к)) = 2 × 206,3 – (130,6 + 116,1) =

=165,9 Дж/К. Т = 53100 Дж: 165,1 Дж/К = 320,1 К.

Приклад 6. Використовуючи табличні дані, обчисліть ентальпію розкладу 4 г NaOH. DН⁰₂₉₈ (NaOH) = – 426,6 кДж/моль.

Розв’язання. Із закону Лавуазьє-Лапласа випливає, що ентальпія розкладу дорівнює ентальпії утворення зі зворотним знаком: – DН⁰_утв. (NaOH) = = DН⁰_розкл. (NaOH). Знаючи, що DН⁰₂₉₈ відноситься до 1 моль, визначимо число молів NaOH: n = m (NaOH)/ M (NaOH) = 4: 40 = 0,1 моль. Таким чином, ентальпія розкладу 4 г NaOH: DН⁰_розкл. (NaOH) = 426,6 × 0,1 = 42,66 кДж.

Приклад 7. Теплота (DН⁰) утворення НСl становить – 92,3 кДж/моль. Обчисліть енерґію зв’язку Н–Сl, якщо відомо, що енерґії дисоціації молекул Н₂ та Сl₂ на атоми становлять 43,6 і 242,6 кДж/моль відповідно.

Розв’язання. Процес утворення молекул НСl із простих речовин можна подумки розбити на стадії: 1) дисоціація молекул Н₂ та Сl₂ на атоми; 2) утворення молекул НСl із атомів. 1) ½Н₂ = H; DН=½DН_дис. (Н₂);

½Сl₂ = Сl; DН = ½DН_дис. (Сl₂);

2) ½Н₂ + ½Сl₂ = НСl ; DН = DН⁰_утв.. (НСl);

У відповідності з законом Ґесса алгебраїчна сума теплових ефектів проміжних стадій утворення НСl із простих речовин дорівнює ентальпії утворення НСl: ½DН_дис. (Н₂) + ½DН_дис. (Сl₂) + DН (Н–Сl) = DН⁰_утв. (НСl);

DН (Н–Сl) = DН⁰_утв. (НСl) – ½(DН_{дис .} (Н₂) + DН_дис. (Сl₂)) =

= – 92,3 – ½(43,6 + 242,6) = – 431,6 кДж/моль.

Отже, енерґія зв’язку Е (Н–Сl) = – 431,6 кДж/моль.

Приклад 8. Визначте енерґію зв’язку гідроґен-оксиґен у молекулі Н₂О, якщо енерґії зв’язків Н–Н і О–О відповідно становлять 435,9 і 498,7 кДж/моль, а при згорянні 2 моль водню виділяється 483,68 кДж теплоти.

Розв’язання. Процес утворення води можна подати наступним чином: руйнуються зв’язки Н–Н і О–О, а утворені атоми гідроґену та оксиґену сполучаються у молекули Н₂О, кожна з яких містить два зв’язки Н–О.

1) 2Н₂(г) = 4H(г); DН₁ = 2 × (– 435,9 кДж/моль);

О₂(г) = 2О(г); DН ₂ = – 498,7 кДж/моль;

2) 2Н₂(г) + О₂(г) = 2Н₂О(г); DН = 2 DН⁰_утв. (Н₂О) = 2 × (– 483,68 кДж/моль);

4Н(г) + 2О(г) = 2Н₂О(г); DН = – 1854,18 кДж.

У двох молекулах Н₂О 4 зв’язки гідроґен-оксиґен, отже середня енерґія зв’язку гідроґен-оксиґен Е (Н–О) = (– 1854,18 кДж): 4 = – 463,54 кДж.

Глава 6. ХІМІЧНА КІНЕТИКА.

Для відповіді на найважливіше для хіміка питання – перебігатиме чи не перебігатиме та чи інша реакція? – необхідно оцінити можливість її перебігу не лише з точки зору термодинаміки, але й також одержати про її швидкість, її кінетику. Про принципову здійсненність процесу судять за значенням зміни енерґії Ґіббса у системі. Однак це значення нічого не говорить про реальну можливість перебігу реакції у даних конкретних умовах, не дає ніякої уяви про швидкість і механізм процесу. Наприклад, взаємодія нітроґен (ІІ) оксиду із киснем:

2NO(г) + O₂(г) → 2NO₂(г); ΔG = – 70 кДж,

перебігає дуже швидко при кімнатній температурі, у той час як реакція:

2Н₂(г) + O₂(г) → 2Н₂О(г); ΔG = – 458 кДж,

що характеризується значно більшим зменшенням енерґії Ґіббса, за звичайних умов практично не перебігає. Суміш водню з киснем зберігає ся при кімнатній температурі без помітної взаємодії дуже тривалий час, але у присутності каталізатора чи при 700^оС процес перебігає практично миттєво (з вибухом).

Таким чином для повного опису хімічної реакції необхідно знати також закономірності її перебігу за часом, тобто її швидкість і детальний механізм. Швидкість і механізм хімічних реакцій вивчає хімічна кінетика.

Перебіг будь-якої реакції можна подати схемою:

Вихідні реаґенти → Проміжні речовини → Продукти реакції.

(перехідний стан)

Виявлення та дослідження перехідного стану, що не має ніякого значення для обчислення ΔН_r, ΔS_r і ΔG_r процесу, але визначає швидкість реакції є складною проблемою, оскільки проміжні продукти вдається виділити та дослідити досить рідко. У більшості випадків механізм процесу й, особливо, характер перехідного стану є результатом більш чи менш правдоподібної гіпотези.

6.1. Поняття про швидкість хімічної реакції

Вихідним та наріжним поняттям хімічній кінетиці є поняття про швидкість хімічної реакції.

Швидкість хімічної реакції дорівнює зміні кількості речовини за одиницю часу в одиниці реакційного простору. У залежності від типу хімічної реакції (гомоґенна чи гетероґенна) змінюється характер реакційного простору. Гомоґенною реакцією називається реакція, що перебігає в однорідному середовищі (одній фазі). Гетероґенні реакції перебігають на межі поділу фаз, наприклад твердої та рідкої, твердої та газоподібної, двох рідких, що обмежено змішуються, тощо. Реакційним простором гомоґенних реакцій є об’єм, заповнений реагуючими речовинами. Оскільки відношення кількості речовини до одиниці об’єму називається концентрацією (С), то швидкість гомоґенної реакції дорівнює зміні концентрації продуктів чи вихідних речовин за часом. Розрізняють середню та миттєву швидкості реакції.

Середня швидкість реакції ávñ визначається за формулою:

ávñ = ± 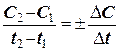(6.1.)

де С₂ та С₁ концентрації вихідної речовини (чи продукту реакції) у моменти часу t₂ та t₁. Якщо у рівнянні стоїть концентрація вихідної речовини, яка зменшується, то перед відношенням має стояти мінус, якщо ж у рівнянні розглядається концентрація продукту, яка з часом зростає, то має бути плюс.

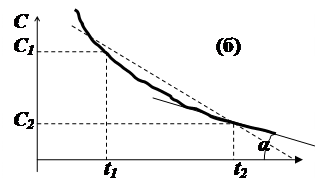
Концентрація вихідної речовини (С) в залежності від хімічної природи взаємодії може змінюватися з часом як лінійно, та і відповідно до більш складних закономірностей (параболічних, гіперболічних, експоненційних, тощо). Для лінійної залежності середня швидкість однозначно характеризує перебіг процесу (мал.6.1(а)), оскільки вона визначається танґенсом кута нахилу прямої до осі часу (ΔC/Δt = tg (α)).

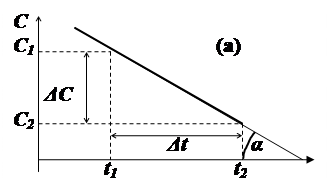Для нелінійної залежності концентрації від часу (мал.6.1(б)) середня швидкість є грубим наближенням, оскільки в інтервалі часу t₂ – t₁, вона не залишається сталою.

Мал..6.1. Залежність концентрації реагуючої речовини від часу для

лінійного (а) та нелінійного (б) процесів.

Чим менше інтервал часу Δt, тим ближче значення середньої швидкості процесу до її істинного значення у момент часу t. У граничному випадку Δt → 0 одержимо: v = 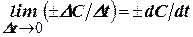(6.2.)

Таким чином, істинна швидкість реакції (v)дорівнює першій похідній від концентрації за часом і визначається тангенсом кута нахилу дотичної до графіка С = f(t) у точці, що відповідає даному моментові часу dC/dt = tg(α).

Швидкість реакції вважається завжди додатною, тому похідна концентрацій вихідних речовин береться зі знаком мінус, а продуктів реакції – зі знаком плюс.

З визначення швидкості реакції випливає, що швидкість реакції у SI має одиницю вимірювання [моль · м^-3 · с^-1], однак також використовуються й інші одиниці вимірювання [моль · л^-1 · с^-1], [моль · см^-3 · с^-1], [моль · см^-3 · хв^-1], тощо.

На швидкість реакції впливає багато чинників: концентрація реаґентів, температура, природа реагуючих речовин, тиск (для реакцій із газами), каталізатори. Окрім того на перебіг реакцій впливають: форма та матеріал посудини (для ланцюгових реакцій), ступінь подрібнення реаґентів (для гетероґенних реакцій), природа розчинника для реакцій у розчинах, швидкість перемішування, освітлення та інші дії електромагнітних полів.

6.2. Основний закон хімічної кінетики – закон діючих мас.

Норвезькі хіміки К.Гульдберг і П.Вааге у 1879 році запропонували загальний вираз кінетичної форми закону діючих мас, який базується на положенні, що швидкість реакції визначається ймовірністю зіткнення реагуючих частинок.

Згідно законові діючих мас швидкість необоротної реакції:

аА + bB → продукти (6.3.)

що перебігає при сталій температурі у гомоґенному середовищі та в одну стадію, пропорційна добуткові концентрацій реагуючих речовин, узятих у ступенях їхніх стехіометричних коефіцієнтів:

v = k · C_A^a · C_B^b, (6.4.)

де C_А та C_B – концентрації реагуючих речовин, а a та b стехіометричні коефіцієнти у даному рівнянні реакції; k – коефіцієнт пропорційності, який було визначено як константу швидкості реакції. Рівняння (6.4.) називається кінетичним рівнянням реакції (6.3.)

Фізичний зміст константи швидкості стає зрозумілим, якщо прийняти, що C_А = C_B = 1 моль/л, тоді v = k, тобто константа швидкості – це швидкість реакції при концентраціях реагуючих речовин рівних одиниці. Константа швидкості реакції k не залежить від концентрації реаґентів, але залежить від їхньої природи та температури.

Межі застосування закону діючих мас.

Закон є справедливим:

1) для найпростіших реакцій, тобто таких що перебігають в одну стадію; якщо реакція перебігає у кілька стадій, то загальна швидкість реакції визначається швидкістю найповільнішої стадії;

2) для реакцій, що перебігають у газовій фазі, лише у межах застосовності законів ідеальних газів;

3) для реакцій, що перебігають у розчинах, тільки при великих розведеннях (низьких концентраціях) розчинених речовин.

6.3. Молекулярність реакції.

Хімічні реакції поділяють на елементарні (одностадійні) та складні (багатостадійні).

Механізм реакції описується таким поняттям як молекулярність реакції. Число молекул, яке беру участь у елементарному акті хімічної взаємодії, називається молекулярністю реакції.

Мономолекулярна реакція – реакція, в елементарному акті якої бере участь одна молекула. Наприклад: Н₂(г) → 2Н(г); v = .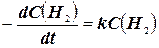

Бімолекулярна реакція – реакція, в елементарному акті якої беруть участь дві молекули, наприклад: 2НІ(г) → Н₂(г) + І₂(г); v = .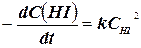

Тримолекулярна реакція – реакція, в елементарному акті якої беруть участь три молекули, наприклад:

Cl₂(г) + 2NO(г) → 2NOCl(г); v = k C( Cl₂ )C( NO )²;

2NO(г) + Н₂(г) → N₂O(г) + Н₂О(г); v = k C( NO )²C( Н₂ );

2NO(г) + О₂(г) → 2NО₂(г); v = k C( NO )²C( О₂ ).

Тримолекулярні реакції дуже рідкісні, оскільки одночасне зіткнення трьох молекул дуже малоймовірне. Молекулярності реакцій вище трьох невідомі. Молекулярність реакції являє собою молекулярно-кінетичну характеристику системи.

6.4. Порядок реакції.

Поняття про порядок реакції випливає з формально-кінетичного опису. Показник ступеню концентрації реагуючої речовини у кінетичному рівнянні:

аА + bB → продукти; v = k · C_A^a · C_B^b

Коефіцієнти a та b називаються порядками реакції за даною речовиною А чи В, відповідно. Загальним порядком хімічної реакції чи просто порядком реакції називається величина, що дорівнює сумі показників ступенів концентрацій реаґентів у кінетичному рівнянні реакції (для даної реакції ця величина дорівнює a + b).

Для простих гомоґенних реакцій, що перебігають в одну стадію порядок і молекулярність співпадають. Для складних реакцій, які перебігають у декілька стадій, у яких можуть брати участь не лише молекули, а й іони, вільні радикали, активні комплекси, порядок реакції з молекулярністю чисельно не співпадає.

У випадку складних реакцій рівняння реакції лише фіксує вихідний та кінцевий стани системи, не розкриваючи механізму процесу. Для багатостадійних реакцій порядки реакцій за реаґентами, як правило не співпадають зі стехіометричними коефіцієнтами, а загальний порядок не дорівнює сумі стехіометричних коефіцієнтів. У випадку складних реакцій різноманітні елементарні стадії накладаються одна на одну, даючи складну концентраційну залежність швидкості.

Кінетичне рівняння вигляду (6.4.) не має універсального характеру: не завжди швидкість реакції є ступеневою функцією концентрації, іншими словами, не завжди існує порядок реакції. Останній має фізичний зміст молекулярності лише для елементарних реакцій. В усіх інших випадках це емпіричний параметр, що показує залежність швидкості сумарного процесу від концентрацій реаґентів.

Тому існують реакції нульового порядку, наприклад каталітичний розклад аміаку на поверхні вольфраму:

NН₃(г) – cat W → ½N₂(г) + 1½Н₂(г);

v = k; розклад NН₃ відбувається на поверхні каталізатора (W) й швидкість розпаду NН₃ не залежить від його концентрації в об’ємі. З цієї ж причини бувають реакції дробового порядку, наприклад, при багатостадійних процесах, якщо найбільш повільні стадії мають різний порядок, але їхні швидкості співставні. Наприклад швидкість реакції СО(г) + Cl₂(г) → COCl₂(г) описується емпіричним рівнянням: v = kС (СО) С (Cl₂)^3/2, згідно з яким порядок реакції за Cl₂ становить 3/2, а загальний порядок реакції дорівнює 5/2. Причиною порушення простої залежності (6.4.) є участь у реакції її продуктів, наприклад, у якості каталізаторів. Прикладом такої реакції може слугувати синтез бромоводню: Н₂(г) + +Br₂(г) → 2HBr(г), яка спочатку описується рівнянням: v = kС (Н₂) С (Br₂)^1/2, а потім, коли утворюються значні кількості бромоводню:

v = k₁ С (Н₂) С (Br₂)^3/2 /(k₂С (Br₂) + C (HBr) ).

Експериментальна оцінка формального порядку має велике значення у хімічній кінетиці, оскільки дозволяє припустити ймовірний механізм перебігу реакції.

6.5. Особливості кінетики гетероґенних реакцій.

Гетероґенні реакції йдуть на поверхні поділу фаз, яка й слугує реакційним простором (поверхнею). Тому першою особливістю кінетики цих реакцій є вплив площі реакційної поверхні на швидкість реакції. Якщо сумарна площа поверхні дорівнює S, то загальна швидкість гетероґенної реакції першого порядку описується рівнянням:

v = kСS, (6.5.)

де C – концентрація реаґента (газоподібного чи рідкого).

Одиниці вимірювання швидкості та константи швидкості гетероґенної реакції відрізняються від одиниць вимірювання відповідних величин гомоґенної реакції. Одиниця вимірювання швидкості гетероґенної реакції – [моль · с^-1], константи швидкості реакції першого порядку – [моль · с^-1]. Якщо у реакції безпосередньо бере участь тверда речовина (або інша рідка фаза), то у кінетичне рівняння не входить його концентрація оскільки вона є сталою. Роль твердого тіла у кінетиці відображують шляхом введення у кінетичне рівняння площі поверхні цього тіла, на якій іде реакція. Наприклад, кінетика гетероґенної реакції:

СаО(к) + СО₂(г) → СаСО₃(к) описується рівнянням v = k С (СО₂) S.

Іноді важливо знати питому швидкість реакції віднесену до одиниці площі реакційної поверхні, яка для реакції першого порядку описується рівнянням: v = v/S = kС. В одиницю вимірювання питомої швидкості реакції входять одиниця вимірювання площі, наприклад [моль · м^-2 · с^-1].

Швидкість деяких гетероґенних реакцій не залежить від концентрації реаґентів у розчині, але в ході реакції зменшується їх концентрація у зоні реакції С_S у порівнянні з їх концентрацією в об’ємі C_V з-за витрати реаґентів. Тому у рівняння швидкості реакції входить концентрація реаґента реакції С_S:

v = k С_S S або v_S = kC_S.

Тому швидкість гетероґенної хімічної реакції залежить від швидкості підведення реаґентів у зону хімічної реакції, що є другою особливістю цих реакцій.

6.6. Механізм хімічних реакцій.

Знання кінетичних рівнянь та їхніх констант дуже корисне для розуміння механізму хімічних реакцій, тобто послідовностей перебігу найпростіших (елементарних) стадій утворення короткоживучих проміжних частинок (інтермедіатів) реакції. Визначення механізмів хімічних реакцій є найважливішим фундаментальним завданням хімії.

Усі реакції можна поділити на прості та складні. Прості реакції перебігають в одну стадію та називаються одностадійними. Складні реакції йдуть або послідовно (багатостадійні реакції), або паралельно, або послідовно паралельно. У свою чергу, у кожній стадії реакції може брати участь одна молекула, дві молекули чи три молекули.

Одностадійні реакції. Відносно невелике число реакцій перебігає в одну стадію. До одно стадійних реакцій відносяться, наприклад,

- реакції дисоціації: Н₂ → 2Н; Cl₂ → 2Cl; 2HI → H₂ + I₂;

- взаємодія йоду та водню: H₂ + I₂ → 2НІ;

- взаємодія нітроґен монооксиду з воднем та озоном:

2NO + H₂ → N₂O + H₂O; NO + O₃ → NO₂ + O₂.

Одностадійні реакції, як і складні, перебігають через утворення активованого комплексу.

Складні реакції. До складних відносяться реакції, що перебігають послідовно (через кілька стадій) або паралельно. Більшість реакцій є багатостадійними.

Послідовні реакції – пов’язана система реакцій, у яких продукт попередніх стадій витрачається у наступних. Наприклад реакція:

2N₂O₅ → 4NO₂ + O₂

перебігає через наступні стадії:

N₂O₅ ↔ NO₂ + NO₃ (швидка реакція);

NO₂ + NO₃ → NO₂ + NO + O₂ (повільна реакція);

NO + NO₃ → 2NO₂ (швидка реакція).

Швидкість лімітуючої реакції (друга стадія) визначає швидкість усієї складної реакції, що розглядається. Швидкість даної реакції дорівнює:

v = k С (N₂O₅).

Паралельні реакції – пов’язана система реакцій, що мають одні й ті ж вихідні реаґенти, але відмінні продукти реакції. Наприклад реакція розкладу KClO₃ може йти двома паралельними шляхами:

4KClO₃ ® .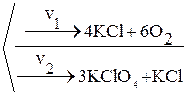

Кожна з реакцій мономолекулярна (в одиничному акті розкладу бере участь одна формульна одиниця KClO₃). Таким чином v₁ = k₁С (KClO₃),

v₂ = k₂С (KClO₃). Сумарна ж швидкість процесу v становитиме:

v = v₁ + v₂ = (k₁ + k₂)С (KClO₃).

Спряжені реакції. Якщо з одним і тим же реаґентом одночасно взаємодіє дві чи більше речовин, то такі реакції називаються спряженими, наприклад: А + В → АВ; A + D → AD.

У деяких випадках спряження реакцій може викликати їх прискорення. Прискорення може бути спричинене утворенням інтермедіатів у перебігу однієї з реакцій, які прискорюють іншу реакцію. Наприклад:

6FeO + 2H₂CrO₄ → 3Fe₂O₃ + Cr₂O₃ + 2H₂O;

6HI + 2H₂CrO₄ → 3I₂ + Cr₂O₃ + 5H₂O.

НІ безпосередньо не взаємодіє з H₂CrO₄.

Спряження реакцій може впливати на термодинаміку процесів. Наприклад, якщо для реакцій: А + В → АВ; ∆G₁ > 0; A + D → AD; ∆G₂ < 0;

|∆G₂ | буде більше |∆G₁ |, то у цих умовах стає можливим перебіг першої реакції, оскільки енерґія Ґіббса сумарної реакції буде менше нуля:

2А + В + D → АВ + AD; ∆G_Σ < 0.

Багато біохімічних реакцій, особливо у живих орґанізмах перебігають за механізмом спряжених хімічних реакцій.

Ланцюгові реакції – пов’язана система складних реакцій, що перебігають послідовно, паралельно та спряжено з участю вільних радикалів. Швидкість їх залежить від природи та об’єму посудини, для деяких із них характерний поріг тиску, нижче якого реакція не відбувається. За певних умов реакція прискорюється лавиноподібно. Вперше ідею про можливість ланцюгового механізму висловив російський вчений М.О.Шилов у 1905 році. Великий внесок у розробку теорії ланцюгових реакцій внесли М.М.Семенов (Росія) та С.Гіншельвуд (Велика Британія).

Ланцюгові реакції починаються зі стадії ініціювання, тобто утворення активних частинок – вільних радикалів. Вільні радикали являють собою уламки молекул, що мають неспарені електрони. Деякі вільні радикали є стабільними речовинами за звичайних умов, наприклад ·ClO₂, Ph₃C·, тощо (вільним бірадикалом є навіть молекула кисню), інші – при

Дата добавления: 2014-10-15