Пересечение прямой линии общего положения с плоскостью общего положения

Точку пересечения прямой с плоскостью общего положе­ния (рис. 4.10, а) строят в следующем порядке (рис. 4.10, б):

а) через заданную прямую АВ проводят вспомогательную плос­
кость Т;

б) строят линию пересечения 1—2 вспомогательной плоско­
сти Т и заданной плоскости Q;

в) в пересечении построенной линии 1—2 с заданной прямой
АВ отмечают искомую точку К.

На рисунке 4.11 дано построение на чертеже проекций точки
пересечения прямой, заданной проекциями d'e', de, с плос­
костью общего положения, задан­
ной проекциями a'b'c', abc тре­
угольной пластины. Проекции _в А.
точки пересечения строят в следу- / М-^:$\
ющем порядке: а/ гд жУ

через прямую DE проводят / / ~) /\Ш/~) вспомогательную плоскость, на- / 6_К / /. кЩ/ /

пример фронтально-проецирую- ^-------- ' *-------- у~/

щую Р (на рис. 4.11, б показан _а) 6)

только след Д); Рис. 4.ю

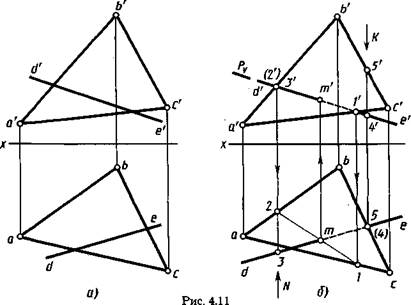
строят проекции 1'2', 1—2 линии пересечения этой плос­кости с плоскостью треугольника, заданной проекциями а'Ь'с', abc; при этом по фронтальным проекциям точек Г и 2' нахо­дят горизонтальные проекции точек 1 и 2;

находят проекции т', т точки пересечения заданной пря­мой с плоскостью треугольника. Для этого в пересечении про­екций de и 1—2 отмечают горизонтальную проекцию т искомой точки и с помощью линии связи строят ее фронтальную проек­цию т' на проекции d'e' прямой. Прямые БЕи 1—2 пересека­ются, так как принадлежат одной плоскости Р;

определяют видимые участки прямой DE.

Для определения видимых участков прямой DE анализируют положение точек на скрещивающихся прямых. Так, точки с проекциями 3', 3 и 2', 2 находятся на скрещивающихся пря­мых с проекциями d'e', de и a'b', ab соответственно. Их фрон­тальные проекции 2' и 3' совпадают. По горизонтальной проек­ции при взгляде по стрелке N видно, что точка 3 находится перед точкой 2, т. е. она закрьшает точку 2. Следовательно, прямая DE слева от точки М расположена перед треугольником ABC Поэтому фронтальная проекция d'm' ее показана как видимая. От точки М вправо прямую DE закрьшает треугольник ABC до точки 7, соответственно отрезок т'Г показан как невидимый.

Невидимый участок на горизонтальной проекции прямой DE выявляют анализом положения точек с проекциями 5', 5 и 4', 4, лежащих на скрещивающихся прямых с проекциями b'c', be и d'e', de. По фронтальной проекции очевидно, что если смотреть по стрелке К, то вначале видят точку 5, распо­ложенную выше точки 4. Она закрывает точку 4. Следователь­но, в этом месте прямая DE закрыта треугольником ABC до точки их пересечения М (участок с проекцией т—5). Слева от точки пересечения М прямая DE находится над треугольником ABC и, естественно, видима (участок с проекцией dm).

Дата добавления: 2014-11-06