Прямые особого положения в плоскости — главные линии плоскости

К прямым, занимающим особое положение в плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций. Эти линии на­зывают главными линиями плоскости.

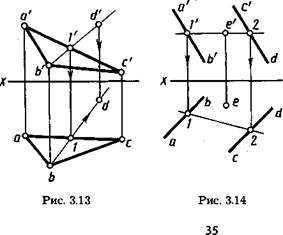
Горизонталь— прямая, лежащая в плоскости и параллельная плоскости проекций Н. На рисунке 3.15 проекции горизонтали проведены через проекции с', с точки С и Г, 1 точки 1 прямой АВ плоскости, заданной проекциями точки С и прямой АВ. Фронтальная проекция с', Г горизонтали параллельна оси х.

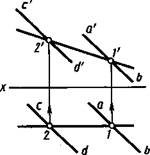
Фронталь — прямая, лежащая в плоскости и параллельная плоскости проекций V. На рисунке 3.16 проекции фронтали проведены через проекции Г, 1 и 2', 2 точек 1 и 2 проекций а'Ъ', ab, c'd', cd параллельных прямых АВ и СВ заданной

Г ^х	V
	'	V.'
	>	к

Рис. 3.15

плоскости. Горизонтальная проекция 1—2 фронтали параллель­на оси х.

Линиями наибольшего наклона плоскости к плоскостям Н, V и W называют прямые, лежащие в ней и перпендикулярные или к горизонталям плоскости, или к ее фронталям, или к ее про­фильным прямым. Соответственно определяется наклон плос­кости к плоскостям Н, Гили W.

Рассмотрим линию наибольшего наклона к плоскости Н, называемую линией ската.

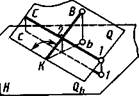
Линия ската ВК плоскости Q и горизонталь С—1 показаны на рисунке 3.17: BK±Q_h. Согласно правилам проецирования прямого угла (см. 1.3, 2.4, рис. 1.10, 2.16) МТ перпендику­лярна Q_h и с—1. Поэтому /LBKb есть линейный угол двугран­ного угла, образованного плоскостями Q и Н. Следовательно, линия ската плоскости может служить для определения угла наклона этой плоскости к плоскости проекций Н. На рисун­ке 3.18 линия ската А— 2 в плоскости треугольника с проекция­ми a'b'c', abc проведена перпендикулярно к горизонтали с проек­циями с'Г, с—1.

Вначале на горизонтальной проекции а проведен перпенди­куляр а—2 к проекции с—1 горизонтали, построена фронталь­ная проекция 2' точки 2 и через нее проведена фронтальная проекция а'2' линии ската.

Рис. 3.16

Рис. 3.17

С'	/}\		Г	Г
					>ь'
X с<	k	\	а	к	>ь

Рис. 3.18

Угол между линией ската и ее горизонтальной проекцией является линейным углом между плоскостью, которой принад­лежит линия ската, и плоскостью проекций Н.

ш

1. Как может быть задана плоскость на чертеже?

2. Что называют следом плоскости на плоскости проекций?

3. Где располагаются фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа плоскости?

4. Как определяют на чертеже, принадлежит ли прямая плоскости?

5. Как строят на чертеже точку, принадлежащую плоскости?

6. Какие линии называют фронталью, горизонталью и линией ската плоскости?

7. Определяет ли прямая линия плоскость, для которой эта прямая является линией ската?

Глава четвертая

Дата добавления: 2014-11-06