Взаимное положение прямых

Как известно, прямые в пространстве могут быть пересека­ющимися, параллельными или скрещивающимися. Рассмот­рим эти случаи.

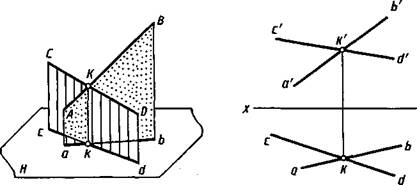
Пересекающиеся прямые. Наглядное изображение двух пря­мых АВ и CD, пересекающихся в точке К, приведено на ри­сунке 2.10, их чертеж в системе V, Н — на рисунке 2.11.

Рис. 2.10 Рис. 2.11

Если прямые пересекаются, то их одноименные проекции пе­ресекаются между собой, а проекции точек пересечения лежат на одной линии связи.

				г
	< b'	i	d'	<	\	f
с>	i				\>^b"
X	^а\	i					У
сХ	к
	ь	i	d	V

Рис. 2.12

Для прямых, кроме профильных, в системе V, Н справед­ливо и обратное утверждение:

если в системе V, Н точки пересечения одноименных проекций прямых, кроме профильных, лежат на одной линии связи, то прямые пересекаются.

Если в системе V, Я одна из рассматриваемых прямых про­фильная, то, чтобы ответить на вопрос, пересекаются ли пря­мые, следует построить их профильные проекции.

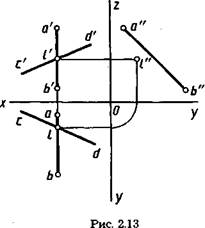
Примеры чертежей пересекающихся и непересекающих­ся (скрещивающихся) прямых, из которых одна с проекци­ями a'b', ab, a"b" — профильная, показаны на рисунках 2.12 и 2.13.

На рисунке 2.12 все три проекции к', к, к" точки Упрямой CD принадлежат и трем одноименным проекциям a'b', ab и а"Ь" прямой АВ, т. е. прямые пересекаются.

На рисунке 2.13 профильная проекция /" точки L прямой CD не принадлежит профильной проекции а"Ь", следователь­но, прямые АВ и CD не пересекаются (см. также рис. 2.7, а).

На рисунке 2.14 показаны прямые, две проекции которых пересекаются в одной точке, а две другие проекции сливаются в одну линию. Это означает, что обе прямые принадлежат плос­кости Р, перпендикулярной плоскости Н (рис. 2.15).

Частный случай ортогональной проекции двух взаимно пер­пендикулярных прямых, из которых одна параллельна плоско­сти проекций, а другая не перпендикулярна ей, рассмотрен в §1.3 (см. рис. 1.10).

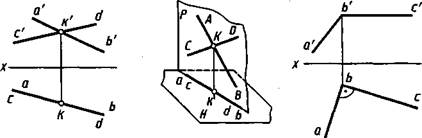
Рис. 2.14 Рис. 2.15 Рис. 2.16

Чертеж прямого угла ABC со стороной ВС, параллельной плоскости Н, приведен на рисунке 2.16. Горизонтальная про­екция Ьа стороны ВА перпендикулярна горизонтальной проек­ции be стороны ВС.

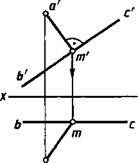
Эта особенность проецирования прямого угла упрощает реше­ние ряда задач. Например, пусть требуется начертить перпенди­куляр из точки с проекциями о', о к прямой с проекциями Ь'с', be, параллельной плоскости V (рис. 2.17). Для этого из точки а' проводим перпендикуляр а'т' к Ь'с'. Построив проекцию т, проводим горизонтальную проекцию am перпендикуляра.

Это свойство будет широко использовано в дальнейшем.

Заметим, что проекция любого угла в зависимости от по­ложения его плоскости может представлять собой острый, пря­мой или тупой угол (или прямую линию, если плоскость угла перпендикулярна плоскости проекций). Если угол не прямой и одна сторона его параллельна плоскости проекций, то на эту плоскость острый угол проецируется также в виде острого угла меньшей величины, тупой угол — в виде тупого угла большей величины.

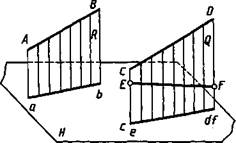
Параллельные прямые. Если в пространстве прямые парал­лельны, то их одноименные проекции параллельны между собой. Действительно (рис. 2.18), проецирующие плоскости Р и Q, проведенные через параллельные прямые АВ и CD, параллель­ны между собой. С плоскостью проекций Н они пересекаются по параллельным прямым ab и cd — проекциям прямых АВ и CD на плоскости Н. Однако из параллельности проекций не всегда следует параллельность прямых.

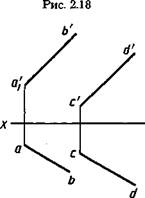
В примере на рисунке 2.19 проекции a'b', e'f, ab, ^"про­фильных прямых АВ и EF между собой параллельны. Однако

из взаимного положения их профильных проекций видно, что сами прямые не параллельны.

Для прямых общего положения эти условия параллельности следующие:

если одноименные проекции прямых общего положения парал­лельны в системе двух плоскостей проекций, то прямые парал­лельны (рис. 2.20).

Для прямых частного положения:

если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой па­раллельны прямые.

По рисунку 2.21 заключаем, что профильные прямые 5—6 и 7—8 параллельны, так как параллельны их профильные про­екции 5" 6" и 7" 8"

Рис. 2.17

ь'	г	а*"
о'<		\	Ч°"
	г		^f>^	у°е"
<	f . 1			У

Рис. 2.19

Рис. 2.20

5'			z 5"
Т 8'		А
6'
X

Рис. 2.21

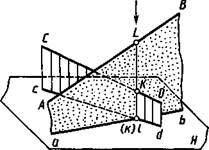
Скрещивающиеся прямые. Скрещи­вающиеся прямые не имеют общих то­чек. Наглядное изображение двух скрещивающихся прямых АВ и CD общего положения дано на рисун­ке 2.22, их чертеж — на рисунке 2.23. С точкой пересечения одноименных проекций аЪ и cd (рис. 2.22) совпада­ют проекции к и / двух точек К и L, принадлежащих различным прямым CD и АВ.

Точки пересечения одноименных проекций скрещивающихся пря­мых не лежат на одной линии связи (рис. 2.23).

Интересен вопрос: какая из изображенных на чертеже пря­мых выше другой или ближе другой к наблюдателю? Это опре­деляют путем анализа положения определенных точек этих прямых.

На рисунке 2.22 видно, что при взгляде сверху по указан­ной стрелке точка L на прямой АВ закрывает точку К (проек­ция точки К на плоскости Н показана поэтому в скобках). Соответственно и на чертеже, приведенном на рисунке 2.23, видно, что фронтальная проекция /' выше фронтальной про­екции к', и при взгляде сверху по стрелке N при проецирова­нии на плоскость # точка L закрывает точку К (горизонтальная проекция к показана в скобках). На плоскости V совпадают фронтальные проекции Г и 2' точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка 1 прямой АВ

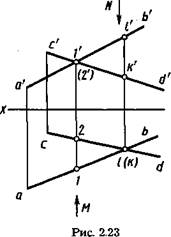
Рис. 2.22

находится ближе к наблюдателю, и при проецировании на плос­кость Гточка 1 прямой АВ закрывает точку 2 прямой CD (фрон­тальная проекция 2' точки 2 показана в скобках).

Рассмотренные точки скрещивающихся прямых, проекции которых на одной из плоскостей совпадают, в литературе иногда называют конкурирующими точками.

Ш

1. При каком положении относительно плоскостей проекций прямую называют прямой общего положения? 2. Как выражается соотношение между проекцией отрезка прямой и самим отрезком?

3. Как расположена прямая в системе Н, V, W, если все три проекции
отрезка этой прямой равны между собой?

4. Как построить профильную проекцию отрезка прямой общего по­
ложения по данным фронтальной и горизонтальной проекциям?

5. Как располагается фронтальная проекция отрезка прямой линии,
если его горизонтальная проекция равна самому отрезку?

6. Как располагается горизонтальная проекция отрезка прямой линии,
если его фронтальная проекция равна самому отрезку?

7. Как разделить на чертеже отрезок прямой линии в заданном отно­
шении?

8. Как построить на чертеже треугольники для определения длины
отрезка прямой линии общего положения и ее углов с горизонталь­
ной и фронтальной плоскостями проекций?

9. Какое свойство параллельного проецирования относится к парал­
лельным прямым?

10. Можно ли по фронтальной и горизонтальной проекциям двух про­
фильных прямых определить, параллельны ли между собой эти
прямые?

11. Как следует истолковать точку пересечения проекций двух скрещи­
вающихся прямых?

12. В каком случае прямой угол проецируется в виде прямого угла?

Глава третья ПЛОСКОСТЬ

Дата добавления: 2014-11-06