К плоскостям проекций

Прямой общего положения и углов его наклона

Определение натуральной величины отрезка

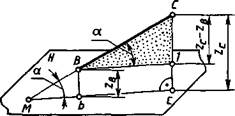
На рисунке 2.8 видно, что натуральная величина отрезка ВС прямой общего положения является гипотенузой прямоуголь­ного треугольника ВС—1. В этом треугольнике один катет В—1 параллелен плоскости Н и равен по длине горизонтальной проекции отрезка ВС ([В—1] ^ [be]), а величина второго кате­та равна разности расстояний точек С и В до плоскости проек­ций Н (| С-1 1 = Zc~Zb=Az).

Построения на чертеже для определения натуральной вели­чины отрезка ВС прямой общего положения приведены на ри­сунке 2.9. В качестве одного катета принята горизонтальная проекция be, длина другого катета |сС|=|с'/'|=Дг. Длина ги­потенузы be равна длине отрезка ВС ([ЬС] ^ [ВС]).

Другое построение выполнено на фронтальной проекции. Проекция Ь'с' отрезка взята за один катет прямоугольно­го треугольника. Длина другого катета равна разности рас­стояний от концов отрезка до плоскости V(\Bb'\~Y_b— Y_c= AY). Длина гипотенузы Be' равна длине отрезка ВС ([Вс'] Ш [ВС]).

	jU^f	с'
'%		■Az
b '	г	У
X		с
uyl	U— Tot

Рис. 2.8

Рис. 2.9

Итак, натуральную величину отрезка определяют как гипо­тенузу прямоугольного треугольника, одним из катетов кото­рого является горизонтальная (фронтальная) проекция отрезка, другим — разность координат концов отрезка до горизонталь­ной (фронтальной) плоскости проекций. Этот метод иногда называют способом прямоугольного треугольника.

Угол между прямой и плоскостью проекций определяется как угол между прямой и ее проекцией на эту плоскость. На рисун­ке 2.8. таким углом между прямой ВСи плоскостью Яявляется угол a (Z-BMb). Угол а равен углу СВ—1, так как одна сторо­на МС общая, а две другие В— 1 и МС параллельны.

Величину угла а определяют из того же треугольника СВ—1, что и натуральную величину отрезка ВС. На рисунке 2.9 пока­зано, что z.oc ^ /LcbC. Угол р наклона прямой к фронтальной плоскости проекций определяется из треугольника Ъ'с'В, по­строенного на фронтальной проекции отрезка: Z.|3 ^ Z. Ъ'с'В.

Дата добавления: 2014-11-06