Проецирование на три взаимно перпендикулярные плоскости проекций

Для полного выявления наружных и внутренних форм слож­ных деталей и их соединений, для решения ряда задач бывает необходимо три и даже более изображений. Поэтому вводят три и более плоскостей проекций.

Система V, Н, W. Введем в систему V, Н третью вертикаль­ную плоскость проекций (рис. 1.18), перпендикулярную к оси х и соответственно к фронтальной и горизонтальной плоско­стям проекций. Ее называют профильной плоскостью проек­ций и обозначают W (см. также рис. 1.12). Такую систему плоскостей проекций называют системой V, Н, W. В этой системе оси проекций z и у являются линиями пересечения профильной плоскости проекций с фронтальной и горизон­тальной. Точка О — пересечение всех трех осей проекций.

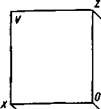
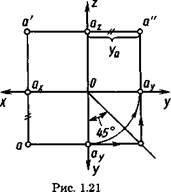
Схема совмещения трех взаимно перпендикулярных плос­костей проекций в одну плоскость чертежа показана на рисун­ке 1.19. При этом ось у занимает два положения. Наглядное изображение некоторой точки А и ее проекции а', а, а" в системе V, Н, W приведено на рисунке 1.20, ее чертеж — на рисунке 1.21.

Профильной проекцией точки называется прямоугольная про­екция точки на профильной плоскости проекций (например, проекция а" на рис. 1.21). Фронтальная и профильная проек-

Рис. 1.18

w

V	N 0	[_90° W
\	\	У
^Л[9Г)
H	У	Рис. 1.19

ции точки (а' и а") лежат на одной линии связи (а'а"), пер­пендикулярной оси z- Профильную проекцию точки строят не­сколькими способами (рис. 1.21).

Через фронтальную проекцию проводят линию связи, пер­пендикулярную к оси z, и от оси z отмечают координату у_а (отрезок аа_х).

Это построение можно выполнить также с помощью дуги окружности, проведенной из центра О, или с помощью пря­мой, проведенной под углом 45° к оси у. Первый из указанных способов предпочтителен как более точный.

Точки в четвертях и октантах пространства. Необходимость использования четвертей и октантов пространства возникает при решении некоторых задач, например при нахождении проекций точки пересечения прямых или прямой и плоскости, которые пересекаются за пределами первого октанта. Плоскости V и Н

У	а' X °х	А	г %	> 'о" (fly
\	е	а	\

Рис. 1.20

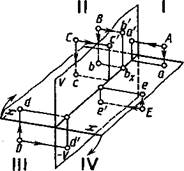
при пересечении образуют четыре двугранных угла, кото­рые называют квадрантами или четвертями пространства. На ри­сунке 1.22, а указан принятый порядок отсчета четвертей I, II, III, IV. Ось проекций делит плоскости Ки Яна полуплос­кости, условно обозначаемые Я и —Я, Уи —V. На рисун­ке 1.22,6 приведен чертеж точек А, В, С, D, Е, расположенных в различных четвертях пространства (рис. 1.22, а).

Точка А расположена в первой четверти. Ее проекции на чертеже (рис. 1.22, 6) аналогичны чертежу на рисунке 1.17. Точка В ближе к V, чем к —Я; на чертеже bb_x<b'b_x. Точка С одинаково удалена от —Я и от V; проекции с' и с совпадают между собой. Точка D расположена в третьей четверти. Гори­зонтальная проекция d получается над осью проекций, фрон­тальная d'— под осью проекций. Точка D расположена от — V дальше, чем от —Я, поэтому на чертеже dd_x>d'd_x. Точка Е расположена в четвертой четверти. Точка Е ближе к Я, чем к — V; е'е_х<ее_х. Точка /"(на рис. 1.22, а не показана) одинако­во удалена от — Ки от Я, поэтому ее фронтальная/' и горизон­тальная/проекции совпадают.

Система из трех плоскостей проекций показана на рисун­ке 1.23. В своем пересечении они образуют восемь трехгранных углов — восемь октантов. Их нумерация — I, II, III, IV, V, VI, VII, VIII — приведена на рисунке 1.23. Из рисунков 1.22, а и 1.23 видно, что четверти пространства нумеруются как I—IV октанты.

Система знаков для отсчета координат х, у* z точек в октантах (в соответствии с рис. 1.23) будет следующая:

Ь'

х —?

d

р

б' f'bf

с' с

о

а'

ьа

а)

6)

Рис. 1.22

октант I (+, +, +);

октант II (+, —, +);

октант III (+, —, —);

октант IV (+, +, —);

октант V (—, +, +);

октант VI (—, —, +);

октант VII (—, —, —);

октант VIII (—, +, —).

VIII

Например, точка (—25; +15; —10) находится в октанте VIII, а точка (—25; —10; —10) — в ок­танте VII.

Рис. 1.23

Проекции точки, располо­женной в I октанте, не могут наложиться одна на другую. Это же относится к точкам, рас­положенным в VII октанте. Для остальных октантов две или все три (для II и VIII октантов) проекции одной и той же точки могут оказаться наложенными друга на друга.

Трехмерное пространство, в котором действуют аксиомы Евклида (III в. до н. э.), стали называть евклидовым пространством.

Дата добавления: 2014-11-06