Центральные проекции и их основные свойства

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Глава первая МЕТОД ПРОЕКЦИЙ

В основе правил построения изображений, рассматривае­мых в начертательной геометрии и применяемых в техническом черчении, лежит метод проекций (от латинского projectio — бросание вперед, вдаль). Изучение его начинают с построе­ния проекции точки, так как при построении изображения любой пространственной формы объекта рассматривается ряд точек, принадлежащих этой форме. Проекцией фигуры назы­вается совокупность проекций всех ее точек.

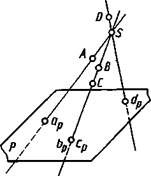
Центральные проекции. При центральном проецировании (по­строении центральных проекций) задают плоскость проекций и центр проекций — точку, не лежащую в плоскости проекций. На рисунке 1.1 плоскость Р — плоскость проекций, точка S — центр проекций.

Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пе­ресечения этой прямой с плоскостью проекций и является центральной про­екцией заданной точки на выбранной плоскости проекций.

На рисунке 1.1 центральной проек­цией точки А является точка а_р пересе­чения прямой SA с плоскостью Р. Так же построены центральные проекции Ь_р, с_р, d_p точек В, С, D на плоскости Р.

Прямые, проходящие через центр
проекций и проецируемые точки, на­
зывают Проецирующими Прямыми. Рис. 1.1

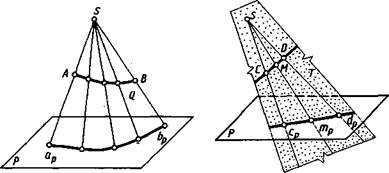
Рис. 1.2 Рис. 1.3

Центральные проекции Ь_р и с_р двух различных точек В и С в пространстве, которые располагаются на одной проецирующей прямой, совпадают. Все множество точек пространства, при­надлежащих одной проецирующей прямой, имеет при одном цен­тре проецирования одну центральную проекцию на заданной плоскости проекций.

Следовательно, при заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну централь­ную проекцию. Но одна центральная проекция точки не позво­ляет однозначно определить положение точки в пространстве.

Для обеспечения обратимости чертежа, т. е. однозначного определения положения точки в пространстве по ее проекции, нужны дополнительные условия, например, можно задать вто­рой центр проекций. Центральным проецированием может быть построена проекция любой линии или поверхности как мно­жество проекций всех ее точек (см. рис. 1.2, 1.3). При этом проецирующие прямые (в своей совокупности), проведенные через все точки кривой линии, образуют проецирующую ко­ническую поверхность (рис. 1.2) или могут оказаться в одной плоскости (см. рис. 1.3), которая называется проецирующей.

Проекция кривой линии представляет собой линию пересече­ния проецирующей конической поверхности с плоскостью про­екций. Так, на рисунке 1.2 проецирующая коническая поверхность Q пересекается с плоскостью проекций Рпо кривой aJo_p, являю­щейся проекцией линии АВ. Однако проекция линии не опреде­ляет проецируемую линию, так как на проецирующей поверхности может быть бесчисленное количество линий, проецирующихся в одну и ту же линию на плоскости проекций (рис. 1.4).

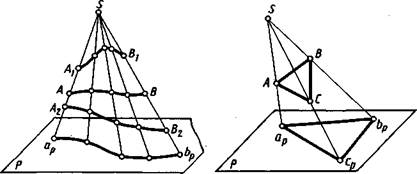
Рис. 1.4 Рис. 1.5

При проецировании прямой линии, не проходящей через центр проекций, проецирующей поверхностью служит плос­кость. Так, на рисунке 1.3 проецирующая плоскость Т, обра­зуемая проецирующими прямыми SCn SD, проходящими через точки Си D прямой, пересекает плоскость проекций Рпо пря­мой c_pd_p, которая и является проекцией прямой CD. Соответ­ственно проекция тп_р точки М прямой CD принадлежит и проекции Cpdp.

Для построения проекций линий, поверхностей или тел ча­сто достаточно построить проекции лишь некоторых характер­ных точек. Например, при построении на плоскости проекций Р проекции треугольника ABC (рис. 1.5) достаточно построить проекции а_р, Ь_р, с_р трех его точек — вершин А, В, С

Дата добавления: 2014-11-06