Параллельные проекции и их основные свойства

Свойства центрального проецирования.

1. При центральном проецировании:

а) точка проецируется в точку;

б) прямая, не проходящая через центр проекций, проеци­
руется в прямую (проецирующая прямая — в точку);

в) плоская (двумерная) фигура, не принадлежащая проеци­
рующей плоскости, проецируется в виде двумерной фигуры (фи­
гуры, принадлежащие проецирующей плоскости, проецируются
вместе с ней в виде прямой);

г) трехмерная фигура отображается двумерной.

2. Центральные проекции фигур сохраняют взаимную при­надлежность, непрерывность и некоторые другие геометричес­кие свойства.

3. При заданном центре проецирования проекции фигуры на параллельных плоскостях подобны.

4. Центральное проецирование устанавливает однозначное соответствие между фигурой и ее изображением, например изображения на киноэкране, фотопленке.

Центральные проекции применяют для изображения пред­метов в перспективе. Изображения в центральных проекциях наглядны, но для технического черчения неудобны, так как не соблюдается метрика.

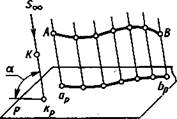
Параллельное проецирование (рис. 1.6) можно рассматри­вать как частный случай центрального проецирования, при котором центр проекций удален в бесконечность (Soo). При па­раллельном проецировании применяют параллельные проецирую­щие прямые, проведенные в заданном направлении относительно плоскости проекций. Если направление проецирования перпенди­кулярно плоскости проекций, то проекции называют прямоуголь­ными или ортогональными, в остальных случаях— косоугольными (на рис. 1.6 направление проецирования указано стрелкой под углом а ф 90° к плоскости проекций Р).

При параллельном проецировании сохраняются все свой­ства центрального проецирования, а также возникают следую­щие новые свойства.

1. Параллельные проекции взаимно параллельных прямых па­раллельны, а отношение длин отрезков таких прямых равно от­ношению длин их проекций.

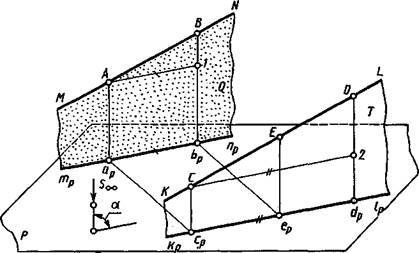
Если прямые MNn XL (рис. 1.7) параллельны, то проеци­рующие плоскости Q и Г параллельны, так как пересекающи­еся прямые в этих плоскостях взаимно параллельны: MN\ KL —

по условию, Аа_р\\ Сс_р\\ Soo. Сле­довательно, проекции т_рп_р и k_pl_p параллельны как линии пересече­ния параллельных плоскостей QnT с плоскостью Р.

Отметим на прямой MN произ­
вольный отрезок АВ и на прямой
KL — произвольный отрезок CD.
Проведем в плоскости Q через точ­
ку А прямую А— 1 1| а_рЪ_р и в плос-
Рис. 1.6 кости Т через точку С — нрямую

Рис. 1.7

С— 2 1| Cpdp. Отрезки [А—1] = [apbp], [С—2] = [Cpd_p] как отрезки параллельных между параллельными. Отрезки C—2\Cpd_p\apb_p и, следовательно, С—2\\А—1. Отрезки В—1\\ D—2\\ Soo, ААВ—1 со A CD—2, так как все их стороны взаимно парал­лельны. Из подобия треугольников АВ—\ и CD—2 следует:

\AB\:\CD\ = \A-l\:\C-2\ = \_apb_p\:\Cpdp\.

Из рассмотренного следует:

а) если длина отрезка прямой делится точкой в каком-либо
отношении, то и длина проекции отрезка делится проекцией
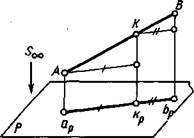
этой точки в том же отношении (рис. 1.8):

\АК\:\КВ\ = \аркр\:\крЬ_р\;

б) проекции равных по длине
отрезков взаимно параллельных
прямых взаимно параллельны и
равны по длине.

Рис. 1.8

Это очевидно, так как (см. рис. 1.7) при \АВ |: | CD \ = 1 бу­дет | а_рЬр\ = | Cpd_p\. Поэтому при косоугольном проецировании

в общем случае параллелограмм, ромб, прямоугольник, квад­рат проецируются в параллелограмм.

2. Плоская фигура, параллельная плоскости проекций, про­ецируется при параллельном проецировании на эту плоскость в такую же фигуру.

3. Параллельный перенос фигуры в пространстве или плос­кости проекций не изменяет вида и размеров проекции фигуры.

Параллельные проекции, как и центральные при одном цен­тре проекций, также не обеспечивают обратимости чертежа. Применяя приемы параллельного проецирования точки и ли­нии, можно строить параллельные проекции поверхности и тела. Параллельные проекции применяют для построения наглядных изображений различных технических устройств и их деталей, например аксонометрических проекций, рассматриваемых ниже.

Дата добавления: 2014-11-06