Положение плоскости относительно плоскостей проекций. Способы задания плоскости на чертеже

Способы задания плоскости на чертеже

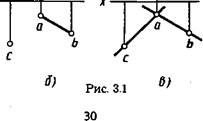
Положение плоскости в пространстве определяется: тремя точками, не лежащими на одной прямой, прямой и точкой, взятой вне прямой, двумя пересекающимися прямыми и дву­мя параллельными прямыми. Соответственно плоскость на чер­теже (рис. 3.1) может быть задана проекциями трех точек, не лежащих на одной прямой (а), прямой и точки, взятой вне прямой (б), двух пересекающихся прямых (в), двух параллель­ных прямых (г). Проекции любой плоской фигуры также могут служить заданием плоскости на чертеже, например на рисун­ке 3.6 дано изображение плоскости проекциями треугольника.

Плоскость относительно плоскостей проекций может зани­мать следующие положения: 1) не перпендикулярна плоско­стям проекций; 2) перпендикулярна одной плоскости проекций; 3) перпендикулярна двум плоскостям проекций.

Плоскость, не перпендикулярную ни к одной из плоскостей проекций, называют плоскостью общего положения (см. рис. 3.1).

а'

о

с'

9 Ь'

о

X ----------------------------

о

■о 6 Ь 6

а)

С' о

а' ф

у /f y V V

а

X

г)

Второе и третье положения плоскостей являются частными случаями. Плоскости в этом положении являются проецирую­щими плоскостями.

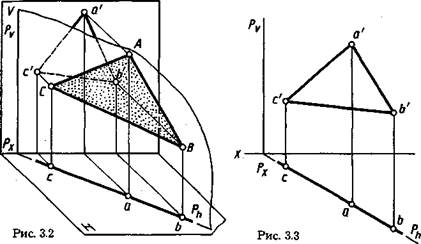
Плоскость перпендикулярна одной плоскости проекций. На­глядное изображение плоскости Р, заданной треугольником ЛВС и перпендикулярной плоскости Н, приведено на рисунке 3.2, ее чертеж — на рисунке 3.3. Такую плоскость называют гори­зонтально-проецирующей.

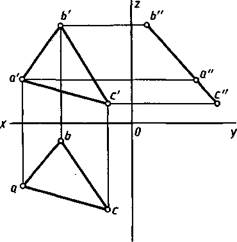
Наглядное изображение плоскости Q, заданной параллелог­раммом ABCD, перпендикулярной фронтальной плоскости про­екций, приведено на рисунке 3.4, ее чертеж — на рисунке 3.5. Такую плоскость называют фронтально-проецирующей.

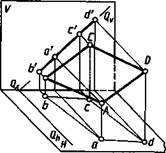
Чертеж плоскости в виде треугольника с проекциями а'Ь'с', abc, a"b"c", перпендикулярной профильной плоскости про­екций, показан на рисунке 3.6. Такую плоскость называют профиль­но-проецирующей.

Следы плоскостей. Линию пересечения плоскости с плоскостью проекций называют следом. Линия пересечения некоторой плоскости х Р, заданной треугольником ABC, с плоскостью Н обозначена P_h, с плоскостью V— P_v (см. рис. 3.2).

Линию пересечения плоскости
с плоскостью Н называют гори- Рис. 3.4

У Рис. 3.6 фронтальным следом,

				d'	У
C'r/
^аЯ
Ь'У
xV
	b,
	\	i
о„		0'	^		<d

Рис. 3.5

зонтальным следом, с плоскостью V с плоскостью W — профильным следом.

Для плоскости Р, перпендикулярной плоскости Н, гори­зонтальный след P_h (см. рис. 3.2, 3.3) располагается под уг­лом к оси х, соответствующим углу наклона этой плоскости к фронтальной плоскости проекций, а фронтальный след Р„ — перпендикулярно оси х.

Аналогично для некоторой плоскости Q, перпендикуляр­ной плоскости V (см. рис. 3.4, 3.5), фронтальный след Q_v располагается под углом к оси х, соответствующим углу накло­на этой плоскости к плоскости Н, а горизонтальный след Q_h — перпендикулярно оси х.

На чертежах тот след, который перпендикулярен оси про­екций, обычно, когда он не участвует в построениях, не изоб­ражают.

Свойство проекций геометрических элементов, лежащих в про­ецирующих плоскостях (см. 1.1, п. 1, в). Проецирующая плос­кость изображается прямой линией на той плоскости проекций, к которой она перпендикулярна. Следовательно, и любая гео­метрическая фигура, лежащая в проецирующей плоскости, про­ецируется на эту плоскость проекций в прямую линию.

Плоскость перпендикулярна двум плоскостям проекций. Если плоскость перпендикулярна двум плоскостям проекций, то она параллельна третьей плоскости проекций. Такую плоскость на-

VI

Ь'

'ШМ&.

Ч

а)

Qv Ь'	Z i	Y'Qw
		V	У
Ь		У

Рис. 3.8

а)

r-'i	Pv
С ' '	'■с
	С	V	У
к	У

6)

Рис. 3.9

зывают горизонтальной (параллельная плоскости Н), фрон­тальной (параллельная плоскости V) и профильной (парал­лельная плоскости W).

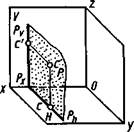
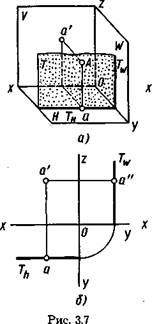
Примеры их наглядных изображений и чертежей приведены на рисунке 3.7, а, б (фронтальная плоскость Г и прнадлежащая ей точка А), на рисунке 3.8, а, б (горизонтальная плоскость Q и принадлежащая ей точка В), на рисунке 3.9, а, б (профильная плоскость Ри принадлежащая ей точка С).

Дата добавления: 2014-11-06