Прямая и точка в плоскости

К числу основных задач, решаемых на плоскости, относят: проведение любой прямой в плоскости, построение в плоско­сти некоторой точки, построение недостающей проекции точ­ки, проверка принадлежности точки плоскости.

Решение этих задач основывается на известных положениях геометрии:

прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости, или через одну точку этой плоскости параллельно прямой, лежащей в этой плоско-

зз

сти или ей параллельной. При этом используется известное условие, что если точка принадлежит плоскости, то ее проек­ции лежат на одноименных проекциях прямой, принадлежа­щей плоскости.

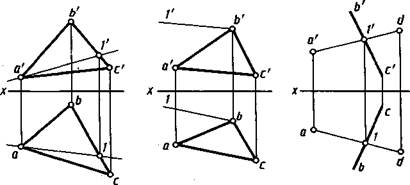
Проведение любой прямой в плоскости. Для этого достаточ­но (рис. 3.10) на проекциях плоскости взять проекции двух произвольных точек, например а', а и Г, 1, и через них про­вести проекции а'Г, а—1 прямой А— 1. На рисунке 3.11 про­екции Ь'Г, Ъ— 1 прямой В— 1 проведены параллельно проекциям а'с', ас стороны А С треугольника, заданного проекциями а'Ъ'с', abc. Прямая В— 1 принадлежит плоскости треугольника ABC.

Построение в плоскости некоторой точки. Для построения в плоскости точки в ней проводят вспомогательную прямую и на ней отмечают точку. На чертеже (рис. 3.12) плоскости, за­данной проекциями а', а точки, b'c', be прямой, проведены проекции а'Г, а—1 вспомогательной прямой, принадлежащей плоскости. На ней отмечены проекции d', d точки D, принад­лежащей плоскости.

Построение недостающей проекции точки. На рисунке 3.13 плоскость задана проекциями а'Ъ'с', abc треугольника. При­надлежащая этой плоскости точка D задана проекцией а". Сле­дует достроить горизонтальную проекцию точки D. Ее строят с помощью вспомогательной прямой, принадлежащей плос­кости и проходящей через точку D. Для этого проводят, на­пример, фронтальную проекцию Ъ'1'd' прямой, строят ее горизонтальную проекцию Ъ—1 и на ней отмечают горизон­тальную проекцию d точки.

Рис. 3.10

Рис. 3.11

Рис. 3.12

Проверка принадлежности точки плоскости. Для проверки принадлежности точки плоскости используют вспомогательную прямую, принадлежащую плоскости. Так, на рисунке 3.14 плоскость Р задана проекциями а'Ъ', аЪ и c'd', cd параллель­ных прямых, точка — проекциями е', е. Проекции вспомога­тельной прямой проводят так, чтобы она проходила через одну из проекций точки. Например, фронтальная проекция Г2' вспомогательной прямой проходит через проекцию е'. Пост­роив горизонтальную проекцию 1—2 вспомогательной прямой, убеждаемся, что точка Е не принадлежит плоскости Р.

Дата добавления: 2014-11-06