Пример определения высоты пирамиды и угла между ее гранями

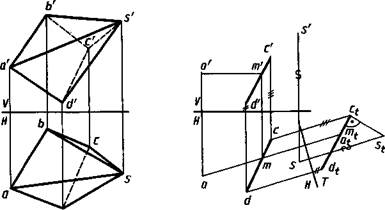
В представленной на рисунке 6.5 пирамиде, основание и грани которой являются плоскостями общего положения, тре­буется определить ее высоту (расстояние от вершины с про­екциями s', s до основания с проекциями a'b'c'd', abed) и двугранный угол между гранями с проекциями a b's', abs и a dY, ads.

Указанные задачи можно решить способом перемены плос­костей проекций, рассмотренным в 5.2.

Определение расстояния от вершины до основания выполне­но на рисунке 6.6. При этом плоскость основания ABCD зада­на проекциями а', а точки и d'c\ dc отрезка. Новая плоскость проекций Т (Т±Н) выбрана перпендикулярной горизонтали с проекциями a'm', am основания (ось ^-±ат) и соответствен­но плоскости основания. На плоскость проекций Т часть ос­нования пирамиды проецируется в отрезок d,c_t, расстояние от которого до проекции s, вершины и соответствует искомой вы­соте пирамиды.

б Рис. 6.5 Рис. 6.6

Определение угла между гранями. Двугранный угол изме­ряют линейным углом, полученным в пересечении граней

двугранного угла плоскостью, перпендикулярной к обеим граням двугранного угла <р, а следователь­но, и к линии их пересечения, т.е. к ребру двугранного угла. Опреде­ление угла ф между гранями пи­рамиды выполнено на рисунке 6.7, где двумя переменами плоскостей проекций ребро с проекциями a s ', as двугранного угла, являющегося отрезком общего положения, пе­реведено в проецирующее положе­ние относительно плоскости проек­ций R. Полученная на плоскости проекций R проекция d_rs_r=a_rb_r двугранного угла выражает его ли­нейный угол.

Рис. 6.7

При преобразовании система плоскостей проекций V, Н замене­на вначале системой H,Q(Q±H),

#11

в которой плоскость Q выбрана параллельной ребру AS (ось ^ || as).

Затем система плоскостей проекций Н, Q заменена на систему Q, R (R±Q), в которой плоскость проекций R выбрана пер­пендикулярной ребру AS (ось ^-±a_qs_q).

Дата добавления: 2014-11-06