Взаимное пересечение многогранников

Построение точек пересечения прямой с поверхностью многогранника

Рис. 6.11

Построение точек пересечения пря­мой с поверхностью многогранника сводится к построению линии пересе­чения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рисунке 6.11 приведено постро­ение проекций е\ е и/'/точек пересечения прямой с проекци­ями т'п\ тп с боковыми гранями пирамиды. Пирамида задана проекциями s', s вершины и a'b'c', abc основания. Прямая MN заключена во вспомогательную фронтально-проецирующую плос­кость T{T_V). Горизонтальные проекции е и/искомых точек по­строены в пересечении проекции тп с горизонтальными проекциями 1—2 и 2—3 отрезков, по которым плоскость Г пе­ресекает боковые грани пирамиды. Фронтальные пооекции е' и/'определены по линиям связи.

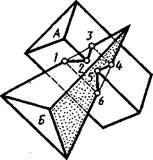
Изображение пересекающихся между собой в пространстве призмы А и пирамиды Б представлено на рисунке 6.12. Линия их пересечения проходит через точки 1, 3, 4, 6 пересечения ребер пирамиды с гранями призмы и точки 2, 5 пересечения ребра призмы с гранями пирамиды. В общем случае в пересе­чении многогранников получается пространственная замкну­тая ломаная линия, которая в некоторых частных случаях может оказаться плоской.

При построении линии пересечения многогранников при­меняют два способа и их комбинации.

1. Строят точки пересечения ребер одного многогранника с гра­нями другого и ребер второго с гранями первого. Через построенные

точки в определенной последовательнос­ти приводят ломаную линию пересече­ния данных многогранников. При этом отрезки прямых проводят лишь через те построенные точки, которые лежат в одной и той же грани.

2. Строят отрезки прямых, по ко­торым грани одной поверхности пере­секают грани другой. Эти отрезки являются звеньями ломаной линии пересечения многогранных поверхно­стей между собой.

Таким образом, построение линии пересечения двух мно­гогранников сводится или к построению линии пересечения двух плоскостей между собой, или к построению точки пере­сечения прямой с плоскостью. Обе эти задачи рассмотрены выше. На практике обычно используют оба способа в комби­нации, исходя из условия простоты и удобства построения.

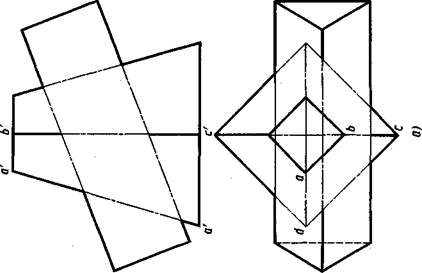
В качестве примера рассмотрим построение линии пересе­чения усеченной правильной четырехугольной пирамиды и на­клонно расположенной трехгранной призмы (рис: 6.13, а). Прежде чем приступить к построениям, анализируют взаим­ное положение многогранников и их расположение относительно плоскостей проекций. В данном случае очевидно, что много­гранники могут пересекаться только по боковым граням. Реб­ра призмы и боковые ребра пирамиды параллельны плоскости V, основания пирамиды параллельны плоскости Н. Нижняя грань призмы и ее основания перпендикулярны плоскости V.

Указанные особенности расположения призмы и пирамиды определяют и наиболее рациональный способ построения ли­нии пересечения их поверхностей по точкам пересечения ребер призмы с гранями пирамиды и боковых ребер пирамиды с гра­нями призмы.

Построения показаны на рисунке 6.13, б. Рассмотрим их для левой части чертежа (от оси пирамиды). Проекции Г, 1, 2\ 2, 3\ 3, 4\ 4 точек пересечения ребер призмы с гранями пирамиды найдены путем проведения через них фронтальных плоскостей Q (Qh), Р (Д), Т {T_h). Они пересекают левые боковые грани пирамиды по фронталям — прямым линиям, параллельным левому ребру пирамиды. Положение их фрон­тальных проекций определено по горизонтальным проекци-

	\ Ч&			-1	«9	•^ ^
		Л
	&	«*	/1л
		/	^
		^ Ь. N
<)			' ^Ч*~^	Ру
			й ^S			г
"о	SU			//	см
	а	.^
	\ *А V^~
			N\	V
	\ \ ^ y**J	^		<*■?
	'^*Ъ			ем

о

S

ям 21, 22 и 24 точек пересечения горизонтальных проекций Qh, Ph ^и T_h плоскостей Q, Р, Тс горизонтальной проекци­ей основания пирамиды. В пересечении фронтальных про­екций этих линий с фронтальными проекциями ребер призмы найдены фронтальные проекции Г, 2' и '/'точек пересече­ния ребер призмы с левыми гранями пирамиды. По ним по­строены горизонтальные проекции 1, 2, 4.

Проекции 3\ 3 точки пересечения ребра AD пирамиды с верхней задней гранью призмы найдены с помощью вспомога­тельной фронтальной плоскости S (S_h), которая проведена через это ребро. Плоскость S пересекает грань призмы по прямой, па­раллельной ребрам призмы и проходящей через точку 23 на осно­вании призмы. В пересечении фронтальных проекций этой прямой и ребра «'^'найдена фронтальная проекция 3 'точки пе­ресечения указанного ребра с задней верхней гранью призмы и на линии связи — горизонтальная проекция 3. С нижней гранью призмы, перпендикулярной плоскости V, ребро AD пересекается в точке с фронтальной проекцией 5' В проекционной связи на проекции ad построена ее горизонтальная проекция 5.

Таким образом, проекции точек пересечения всех ребер призмы с левыми гранями пирамиды Г, 1, 2\ 2, 4\ 4 и ребра AD пирамиды с двумя гранями призмы 3', J? и 5', 5 построены. Соединяем проекции точек, принадлежащих одной грани, и получаем проекции 1'2'3'4'5'Г, 1—2—3 — 4—5—1 ломаной линии пересечения.

Построения в правой части чертежа проекций 6'7'8'9'10'6', 6— 7— 8—9—10— 6линии пересечения аналогичны. Порядок по­строения иллюстрируется стрелками.

Заметим, что переднее и заднее ребра пирамиды не пересе­кают поверхность призмы.

Дата добавления: 2014-11-06