Очевидно, что всегда удовлетворяется условие

Лекция 3. Формулировка понятия устойчивости. Второй (прямой) метод Ляпунова. Теоремы Ляпунова об устойчивости нелинейных систем. Теорема Ляпунова о неустойчивости нелинейных систем.

Формулировка понятия устойчивости

Невозмущенное движение (установившийся процесс) называется устойчивым, если при заданной сколь угодно малой области 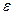(рисунок 3.1) можно найти такую область 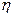, что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходной процесс) будет таким, что изображающая точка не выйдет из области 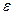при любом сколь угодно большом значении времени .

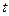Рисунок 3.1

В аналитической записи: Невозмущенное движение (установившийся процесс) будут устойчивым, если при заданном положительном сколь угодно малом числе 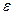можно найти такое положительное число 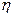(зависящее от заданного 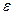), что при начальных условиях

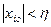
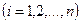(3.1)

Решение дифференциальных уравнений возмущенного движения (переходного процесса) удовлетворяет неравенствам

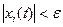
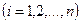
при любом сколь угодно большом значении времени .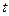

Если в (3.1) величина 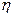принимается достаточно малой, то невозмущенное движение устойчиво в «малом». Если 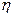- конечная фиксированная величина, то невозмущенное движение устойчиво в «большом». Если же 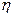может быть любой величиной, то невозмущенное движение устойчиво в «целом». Наконец, будем говорить, что невозмущенное движение абсолютно устойчиво, если оно устойчиво в целом, но не для одной фиксированной характеристики нелинейного элемента, а для некоторого семейства этих характеристик, принадлежащих какому-либо классу.

Второй (прямой) метод Ляпунова

Рассмотренный выше метод фазовых траекторий связан с построением геометрических образов переходных процессов – фазовых траекторий. После построения фазовой траектории становится ясной картина процесса только для принятых при построении начальных условий. Часто требуется определить сходимость переходных процессов в нелинейных системах для некоторой области расположения начальных отклонений или для любых начальных условий. Этому вопросу и посвящены теоремы прямого метода Ляпунова. При рассмотрении этих теорем используются понятия асимптотической и неасимптотической устойчивости. Если фазовые траектории вблизи начала координат стягиваются к нему, то имеет место асимптотическая устойчивость. Если же фазовые траектории вблизи начала координат стягиваются к некоторой особой линии (например, к предельному циклу), то будем иметь неасимптотическую устойчивость.

При рассмотрении прямого метода Ляпунова будем полагать, что движение нелинейной системы описывается n уравнениями первого порядка:

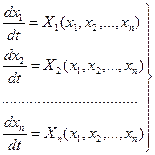, (3.2)

где 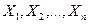- произвольные функции, содержащие нелинейности любого вида; 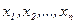- отклонения переменных в переходном процессе от их значений в новом установившемся состоянии, соответствующем значениям внешних воздействий 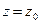(возмущающее воздействие), 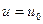(задающее воздействие).

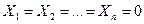при 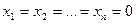, (3.3)

так как в установившемся состоянии все отклонения переменных и их производных равны нулю по самому определению понятия этих отклонений.

Для рассмотрения теорем Ляпунова требуется уяснить вначале понятия о знакоопределенных, знакопостоянных и знакопеременных функциях.

Пусть имеется функция нескольких переменных

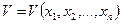. (3.4)

Можно считать, что под знаком нелинейной функции находятся координаты n -мерного пространства 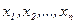. В каждой точке этого пространства функция 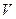будет иметь определенное значение.

Функция 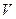называется знакоопределенной, если она во всех точках n -мерного пространства, исключая начало координат, сохраняет один и тот же знак и нигде не обращается в нуль, кроме самого начала координат.

Функция 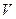называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках пространства.

Функция 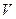называется знакопеременной, если она может иметь разные знаки.

Примеры 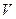-функций: при n =2 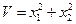- знакоопределенная (положительная) и 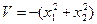- знакоопределенная (отрицательная); 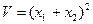- знакопостоянная, так как она может обращаться в нуль не только при 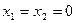, но и при любых значениях 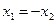. Функция 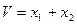будет знакопеременной.

Любую функцию 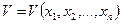тождественно обращающуюся в нуль при 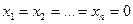, будем называть функцией Ляпунова, если в ней в качестве величин 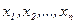взять отклонения переменных исследуемой системы регулирования в переходном процессе, входящие в уравнение (4).

Производная функции Ляпунова по времени будет

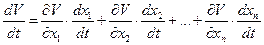. (3.5)

Или, подставив значения производных из заданных уравнений (3.2) в (3.5), получим производную функции Ляпунова по времени в виде

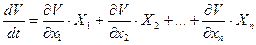, (3.6)

где 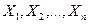- правые части уравнений системы (3.2), представляющие собой заданные функции отклонений.

Следовательно, производная функции Ляпунова по времени, так же как и сама функция, является некоторой функцией отклонений:

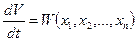. (3.7)

Функция 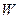, так же как и сама 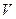, тождественно обращается в нуль при 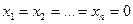. Поэтому к ней можно применять все те же понятия знакоопределенности, знакопостоянства и знакопеременности.

Базируясь на этих предварительных сведениях, дадим общую формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем. Теоремы эти справедливы для любых значений начальных отклонений, для которых справедливы исходные уравнения. То есть с их помощью можно исследовать нелинейные системы на устойчивость в целом.

Теоремы Ляпунова об устойчивости нелинейных систем

Теорема 1. Если существует знакоопределенная функция 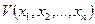, производная 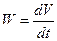которой по времени, взятая в силу дифференциальных уравнений движения (3.2), представляет собой знакопостоянную функцию противоположного с 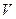знака, то невозмущенное движение устойчиво.

Теорема 2. Если, кроме того, функция 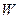знакоопределена, то невозмущенное движение устойчиво асимптотически.

Проиллюстрируем справедливость теорем Ляпунова на наглядном примере.

Возьмем систему второго порядка (n= 2).

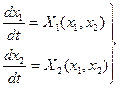. (3.8)

Выберем положительно-определенную функцию Ляпунова в виде

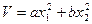, (3.9)

где 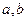- произвольно заданные положительные числа.

Будем придавать величине 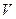возрастающие постоянные значения: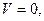 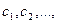что соответствует уравнениям

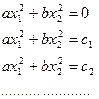. (3.10)

Первое из этих уравнений соответствует одной точке 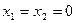началу координат фазового пространства, а остальные – некоторым кривым в фазовом пространстве (рисунок 3.2).

Рисунок 3.2

Если 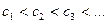, то каждая замкнутая кривая содержит внутри себя начало координат и кривые, соответствующие меньшим значениям 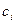. При 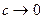кривая стягивается к началу координат, т.е. вырождается в точку 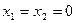. Предположим, нам известно, что при всех возможных траекториях движения изображающей точки она все время переходит с кривой, соответствующей большему значению 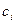функции 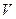, к кривой с меньшим значением функции .

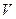Очевидно, что этот факт является достаточным признаком устойчивости системы, поскольку в этом случае все фазовые траектории должны неизбежно кончаться в начале координат.

Аналитически такой характер движения изображающей точки означает, что вдоль фазовых траекторий производная 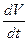функции 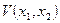отрицательна (см.рисунок 3.5)

.

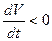Рисунок 3.3 - Асимптотическая устойчивость

Рисунок 3.4 - Неасимптотическая устойчивость

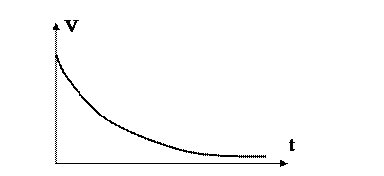
Рисунок 3.5

Производная функции Ляпунова по времени, взятая в силу системы (3.8), имеет вид:

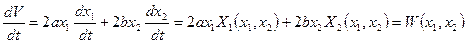
1) Если окажется, что 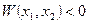, т.е. 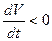, то система асимптотически устойчива

2) Если 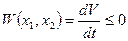, то система просто устойчива.

Пример 1. Пусть нелинейная система описывается следующими уравнениями

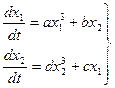(3.11)

Выберем функцию Ляпунова в виде

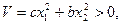(3.12)

Как видно 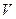- знакоопределенная положительная функция.

Возьмем производную этой функции по времени

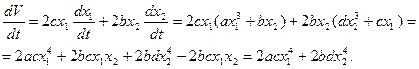
Как видно 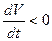, есл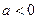и и .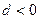

Эти неравенства и есть условия устойчивости системы.

Если 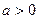, , 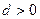то система неустойчива.

Пример 2. Пусть нелинейная система описывается дифференциальным уравнением 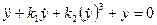. Обозначим , .

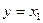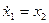Тогда .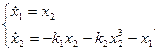

Выберем функцию .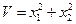

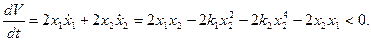
Теорема Ляпунова о неустойчивости нелинейных систем

Если производная 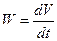по времени от какой-нибудь функции Ляпунова 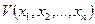, взятая в силу дифференциальных уравнений движения(3.2), окажется знакоопределенной, причем сама функция 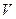будет иметь знак одинаковый со знаком производной 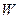, то невозмущенное движение неустойчиво.

Трудность применения метода Ляпунова состоит в том, что отсутствуют общие правила отыскания функции Ляпунова 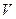. Кроме того он дает только достаточные условия устойчивости. Если для конкретной нелинейной системы удалось найти функцию Ляпунова и с ее помощью определить границы устойчивости системы, то вне этих границ мы ничего не можем сказать об устойчивости системы. Другими словами, мы ничего не знаем о том, какая часть полной области устойчивости нами найдена. Это целиком зависит от того, насколько удачную функцию Ляпунова удалось найти.

Указанные обстоятельства несколько усложняют применение теорем Ляпунова и требуют творческого подхода в подборе функции Ляпунова при исследовании конкретных нелинейных систем.

Литература 1осн [482-483]; [513-519]; 2осн [341-345]; 6доп [194-211].

Контрольные вопросы

1 Что Вы понимаете под понятиями: невозмущенное движение; возмущенное движение?

2 Что Вы понимаете под понятиями устойчивости: в «малом»; в «большом»; в «целом»?

3 Поясните понятия асимптотической и неасимптотической устойчивости.

4 Какие функции называются: знакоопределенными; знакопостоянными и знакопеременными?

5 Дайте формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем.

6 Приведите геометрическую интерпретацию второго метода Ляпунова.

7 Достоинства и недостатки второго метода Ляпунова.

Дата добавления: 2014-11-08