Лекция 5. Приближенные методы исследования устойчивости и автоколебаний. Гармоническая линеаризация нелинейностей. Коэффициенты гармонической линеаризации релейных элементов

Гармоническая линеаризация нелинейностей

Метод гармонической линеаризации – это метод исследования автоколебаний. Он позволяет определить условия существования и параметры возможных в нелинейных системах автоколебаний.

Основы метода гармонической линеаризации в общей его постановке были разработаны в 1934 г. Н. М.Крыловым и Н.Н.Боголюбовым. Применительно задачам ТАУ метод был развит Е.П.Поповым и Л.С.Гольдфарбом. другие его названия – метод гармонического баланса. Метод описывающих функций (по американской терминологии).

Пусть нелинейная система состоит из последовательно включенных нелинейного элемента НЭ и линейной части ЛЧ (рисунок 5.1) и находится в режиме периодических колебаний.

Рисунок 5.1

Сигнал на выходе НЭ периодический, но негармонический и содержит спектр гармонических составляющих. Однако проходя через ЛЧ системы, этот сигнал фильтруется благодаря чему можно пренебречь всеми гармониками выше первой. Это предположение – необходимое условие применения метода гармонической линеаризации, и его называют гипотезой фильтра. Во многих практических случаях гипотеза фильтра выполняется, поскольку высшие гармоники по амплитуде обычно меньше, чем первая гармоника, а ЛЧ, как правило, является фильтром низких частот и подавляет высокочастотные составляющие сигнала.

Сущность метода гармонической линеаризации заключается в замене НЭ эквивалентным линейным звеном, коэффициент передачи которого не является постоянным, а зависит в общем случае от амплитуды и частоты гармонического сигнала на входе НЭ. При рассмотрении устойчивых периодических режимов, когда амплитуды и частоты сигналов принимают фиксированные значения, к исследованию автоколебаний можно применить известные методы анализа линейных САУ.

Рассмотрим простой случай, когда НЭ является безинерционным

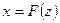(5.1)

Вообще метод гармонической линеаризации применим и к более сложным случаям наличия динамических нелинейностей, а также нескольких нелинейностей в системе.

Пусть входной сигнал отсутствует () и на входе НЭ имеется гармоническое воздействие

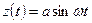. (5.2)

Выходной сигнал НЭ в этом случае будет периодическим, но несинусоидальным и может быть разложен в ряд Фурье:

, (5.3)

где - коэффициенты ряда Фурье, определяемые по формулам:

; (5.4)

; (5.5)

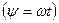, . (5.6)

В практических расчетах этими формулами пользоваться не приходится, так как для типовых нелинейностей имеются готовые соотношения.

Будем полагать, что постоянная составляющая в колебательном процессе отсутствует:

.

Это выполняется, когда нелинейная статическая характеристика является нечетно-симметрической функцией (рисунок 5.2).

Рисунок 5.2

При гармонической линеаризации выходной сигнал НЭ приближенно представляется своей первой гармоникой:

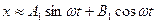. (5.7)

Согласно (5.2)

(5.8)

и после дифференцирования (5.2) по времени:

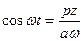. (5.9)

Подставив (5.8),(5.9) в (5.7) получим

или

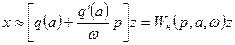, (5.10)

где (5.11)

Соотношение (5.10) линейно связывает входную и выходную величины нелинейного элемента и называется формулой гармонической линеаризации нелинейностей.

Особенностью гармонической линеаризации в отличие от обычной линеаризации является, то, что коэффициенты 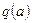и зависят от амплитуды гармонических колебаний (в общем случае и от частоты) на входе нелинейности.

Передаточная функция разомкнутой САУ (рисунок 5.1) определяется:

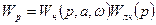. (5.12)

Для исследования линеаризованной системы можно использовать методы линейной теории.

Коэффициенты гармонической линеаризации релейных элементов

Найдем коэффициенты 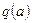и уравнений (5.10) для некоторых типичных релейных элементов по формулам (5.11).

Рисунок 5.3

Возьмем общий вид характеристики НЭ (рисунок 5.3,а), где 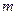есть дробное число в интервале .

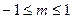Как частные случаи будут получены коэффициенты других релейных элементов.

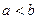Если колебания входной величины имеют амплитуду , то согласно (рисунку 5.3,а) движения в системе не будет. Если амплитуда , то переключения реле происходит в точках (рисунок 5.3,б), в которых имеем

, . (5.13)

Сделаем некоторые вспомогательные выкладки

Для симметричных характеристик в интегралах (5.11) пределы можно брать следующим образом:

,

каждый из них разбивается на три слагаемых:

.

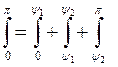Первое и третье слагаемые согласно (рисунку 5.3,а и б) будут равны нулю. Тогда уравнения (5.11) принимают вид

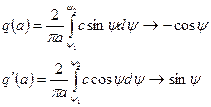
или проинтегрировав получим:

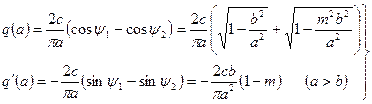(5.14)

Для релейного звена с характеристикой без гистерезисной петли, но с зоной нечувствительности в (рисунок 5.4), учитывая, что здесь 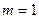из формул (5.14) получаем:

Рисунок 5.4

Для релейного характеристики с гистерезисной петлей (рисунок 5.5), учитывая, что :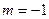

(5.15)

Рисунок 5.5

Для релейного звена (рисунок 5.6), учитывая, что :

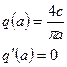(5.16)

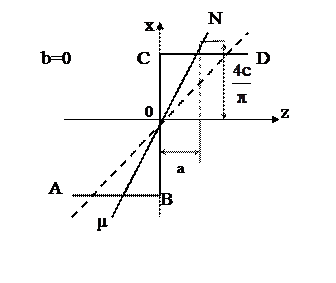
Рисунок 5.6

На последнем примере легко видеть смысл гармонической линеаризации релейной характеристики. Здесь происходит замена ломанной характеристики 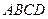прямолинейной 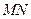приблизительно заменяла собой тот участок ломанной , который охватывается заданной амплитудой .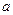

В учебниках имеются таблицы коэффициентов гармонической линеаризации других простейших нелинейных звеньев.

Литература 1осн [533-542]; 2осн [350-358]; 4доп [702-708].

Контрольные вопросы

1 Сущность метода гармонической линеаризации?

2 Поясните понятие гипотезы фильтра.

3 Когда коэффициенты гармонической линеаризации принимают постоянные значения?

4 Напишите соотношение, называемое формулой гармонической линеаризации нелинейностей.

5 Геометрическая интерпретация метода гармонической линеаризации?

Дата добавления: 2014-11-08