Лекция 7. Понятие об импульсных системах. Решетчатые функции и разностные уравнения. Метод Z-преобразования. Передаточные функции импульсных систем

Лекция 6. Некоторые способы определения автоколебаний и устойчивости в нелинейных системах. Применение кривой Михайлова для исследования устойчивости периодических решений. Расчет автоколебаний на основе критерия Найквиста.

Пусть известно дифференциальное уравнение ЛЧ системы

. (6.1)

Уравнение нелинейного звена

.

После гармонической линеаризации

(6.2)

На основании (6.1) и (6.2):

Передаточная функция разомкнутой системы

Передаточная функция замкнутой системы

.

Отсюда гармонически линеаризованное характеристическое уравнение замкнутой линейной системы:

. (6.3)

В случае, когда в замкнутой системе возникают собственные незатухающие колебания с постоянными амплитудой и частотой (автоколебания), коэффициенты 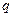и 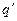становятся постоянными. Из линейной теории известно, что появление указанных колебаний в системе при постоянных коэффициентах соответствует наличию пары чисто мнимых корней в характеристическом уравнении системы. Следовательно,

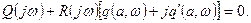(6.4)

выделим в этом выражении вещественную и мнимую части

, (6.5)

и введем для частоты и амплитуды искомого периодического решения обозначения: , .

Это дает два уравнения:

(6.6)

из которых и определяются частота и амплитуда .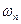

Если уравнения (6.6) не имеют положительных вещественных решений для и 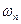, то автоколебания в данной системе невозможны.

С помощью уравнений (6.6) можно строить линии равных значений амплитуды и частоты автоколебаний на плоскости двух каких-либо параметров системы, например, и . Для этого уравнения (6.6) записываются в виде

(6.7)

задаваясь различными числовыми значениями получим зависимости

и

По этим уравнениям в координатах () строим линии (рисунок 6.1).

Рисунок 6.1

На этих кривых получаются отметки частот 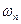, которые также можно соединить (пунктирные линии).

Этот график позволяет выбирать такие значения и , которые соответствовали бы требуемым значениям параметров периодического режима.

Применение кривой Михайлова для исследования устойчивости периодических решений

Ранее указывалось, что не все предельные циклы соответствуют автоколебаниям, а только устойчивые. Обычно в конкретных задачах из физических соображений видно возникают автоколебания или нет. Но в ряде случаев все же приходится этот вопрос исследовать.

Для этого можно использовать кривую Михайлова

, (6.8)

где знак ~ введен, чтобы отличать текущий параметр 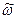, изменяющийся вдоль кривой Михайлова, от частоты 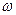, входящей в выражение коэффициентов гармонической линеаризации.

Каждому конкретному значению 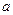будет соответствовать определенная кривая Михайлова. При она пройдет через начало координат (рисунок 6.2).

Рисунок 6.2

Для исследования устойчивости периодического решения дадим малое приращение амплитуде .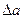

1) Если при 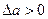кривая Михайлова займет положение 1, а при - положение 2, то переходной процесс в системе будет таким, что колебания с амплитудой, большей чем , затухают, а колебания с амплитудой, меньшей чем , расходятся. Следовательно, переходный процесс с обеих сторон сходится к исследуемому периодическому режиму, т.е. в системе имеют место автоколебания с амплитудой .

2) Если же при 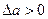получится кривая 2, а при - кривая 1, то исследуемое периодическое решение неустойчиво. Система устойчива в малом и неустойчива в большом.

Расчет автоколебаний на основе критерия Найквиста

Этот метод разработан советским ученым Л.С.Гольдфарбом.

Пусть разомкнутая нелинейная САУ имеет следующий вид (рисунок1).

Рисунок 6.3

Здесь

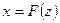, (6.9)

. (6.10)

Согласно формуле гармонической линеаризации

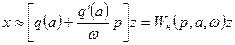. (6.11)

Введем понятие комплексного коэффициента передачи нелинейного звена. Он получается из передаточной функции (6.11) при и зависит только от амплитуды колебаний на его входе:

. (6.12)

Комплексный коэффициент передачи, или частотная передаточная функция линейной части системы:

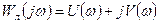. (6.13)

Общая эквивалентная частотная передаточная функция, или АФЧХ разомкнутой системы будет:

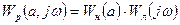. (6.14)

Незатухающие колебания в замкнутой системе определяются, согласно критерию Найквиста, прохождением АФЧХ разомкнутой системы через точку 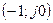(рисунок 6.7), т.е. равенством

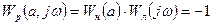. (6.15)

Рисунок 6.4

Это и будет в данном случае условием существования периодического решения для замкнутой нелинейной системы.

Уравнение (6.15) можно привести к виду

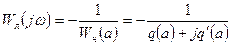. (6.16)

Последнее уравнение просто решается графическим путем. Для этой цели необходимо построить отдельно АФЧХ ЛЧ системы и обратную АФЧХ нелинейного звена, с учетом знака (-) (рисунок 6.5).

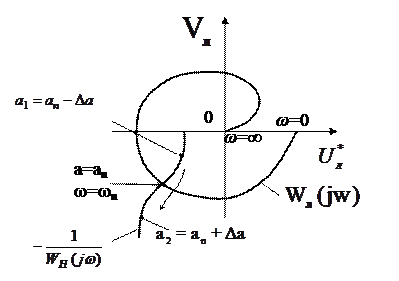
Рисунок 6.5

Точка пересечения этих двух характеристик определяет решение уравнения (6.15). Частота периодического решения находится по отметкам частоты на годографе линейной части 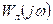, а амплитуда - по отметкам амплитуды на годографе 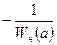нелинейного звена.

Предположим, что линейная часть системы в разомкнутом состоянии устойчива или нейтральна. Тогда исследовать устойчивость периодического решения можно следующим образом. Дадим амплитуде периодического решения некоторое положительное приращение 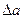. При этом мы сдвигаем по годографу НЗ точку пересечения в сторону роста амплитуд (точка 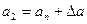). Это соответствует росту модуля , или уменьшению модуля 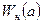. В результате произведение 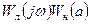уменьшится по модулю и АФЧХ разомкнутой системы 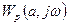(рисунок 6.4) уже не будет проходить через точку 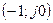, а пройдет так, что эта точка не будет охватываться АФЧХ. Но этот случай соответствует устойчивости системы в том смысле, что процессы в ней должны быть затухающими, т.е. амплитуда колебаний будет уменьшаться.

В случае уменьшения амплитуды (точка 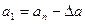) происходит увеличение модуля 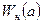и в результате – охват АФЧХ точки 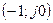,что соответствует появлению неустойчивости и амплитуда колебаний начнет увеличиваться.

Таким образом, при всяком случайном отклонении амплитуды колебаний 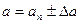она восстанавливает свое значение . Значит, периодическое решение будет устойчивым и соответствовать автоколебаниям.

Формулировку изложенного критерия можно упростить:

Для устойчивости периодического решения требуется, чтобы при переходе годографа 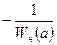из внутренней области годографа 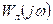во внешнюю происходило возрастание амплитуд, как показано на рисунке 6.5 стрелкой. Если при таком переходе будет убывание значений амплитуд, то периодическое решение неустойчиво.

Возможен более сложный случай, когда годографы ЛЧ и НЗ пересекаются в нескольких точках (рисунок 6.6).

Рисунок 6.6

В этом случае возможны два периодических решения с параметрам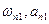и и .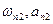

Применяя изложенный выше способ, можно убедиться, первая точка соответствует неустойчивому периодическому решению, а вторая – устойчивому, т.е. автоколебаниям.

Литература 1осн [543-553]; [596-607]; 2осн [359-361]; 4доп [712-725].

Контрольные вопросы

1 Поясните методику построения линий равных значений амплитуды и частоты автоколебаний на плоскости двух параметров системы?

2 Дайте графическую интерпретацию применения кривой Михайлова для исследования устойчивости периодических решений.

3 На основе какого критерия устойчивости был разработан метод исследования автоколебаний Л.С. Гольдфарба?

4 Напишите аналитическое выражение условия существования периодического решения для замкнутой нелинейной системы.

5 Дайте графическую интерпретацию метода Гольдфарба для исследования устойчивости периодически решений и определения параметров колебаний.

Понятие об импульсных системах

В зависимости от способов преобразования сигналов САУ подразделяются на непрерывные и дискретные.

В непрерывных системах сигналы не прерываются.

В дискретных системах имеются элементы, прерывающие непрерывные сигналы и преобразующие их в дискретные.

Процесс преобразования непрерывных сигналов в дискретные называют квантованием.

Различают три способа квантования сигналов: а) по уровню; б) по времени; в) смешанный – по уровню и по времени.

В зависимости от типа квантования дискретные системы подразделяют на релейные(процесс квантования по уровню), импульсные (по времени) и цифровые (смешанные).

Дискретные САУ нашли широкое распространение, так как они характеризуются высокой точностью и помехозащищенностью за счет цифрового представления аналоговых данных и использования процессов прерывания.

В данном разделе рассмотрим только импульсные системы. Большинство замкнутых импульсных САУ можно представить, как показано на рисунке 7.1.

Рисунок 7.1

Здесь НЧ – непрерывная часть системы, а ИЭ – импульсный элемент.

ИЭ осуществляет квантование непрерывного сигнала Х по времени, в дискретный сигнал У.

Квантование, осуществляемое ИЭ в виде преобразования непрерывного сигнала в последовательность импульсов называется импульсной модуляцией.

Выходной сигнал ИЭ имеет прямоугольную форму и характеризуется следующими параметрами (рисунок 7.2):

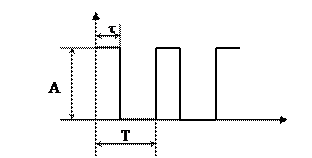
Рисунок 7.2

– высотой, или амплитудой, импульса ;

– длительностью, или шириной, импульса ;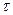

– периодом повторения импульсов ;

– паузой между соседними импульсами ;

– скважностью .

При импульсной модуляции в процессе преобразования непрерывного сигнала в последовательность импульсов указанные параметры импульсов могут изменяться в функции выходного воздействия.

В зависимости от того, какой из параметров импульсного выхода подвергается изменению, различают три вида импульсной модуляции: АИМ, ШИМ, ЧИМ.

Существуют и другие виды импульсной модуляции, однако они применяются лишь в системах связи и поэтому здесь не рассматриваются.

Рисунок 7.3

На рисунке 7.3а, б, в представлены: непрерывный сигнал и соответствующие ему импульсные последовательности при АИМ, ШИМ и ЧИМ.

Как видно из рисунка 7.3, при:

а) АИМ – амплитуда (высота) выходных импульсов изменяются в соответствии с изменениями входного непрерывного сигнала, а длительность 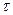и период повторения импульсов остаются неизменными;

б) ШИМ – длительность (ширина) 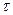выходных импульсов изменяется в соответствии с изменениями входного непрерывного сигнала, а амплитуда и период повторения остаются неизменными;

в) ЧИМ – изменяется частота (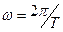) следования импульсов, а размеры импульсов остаются неизменными.

В качестве примера ИЭ, осуществляющего АИМ, рассмотрим рисунок 7.4.

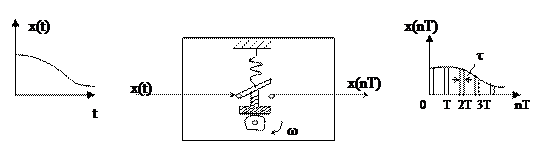
Рисунок 7.4

Ключ периодически замыкается, и на его выходе через равные промежутки времени появляются импульсы, амплитуда которых соответствует величине входного непрерывного сигнала .

Последовательность импульсов, полученная из непрерывного сигнала в результате квантования, является своеобразным промежуточным носителем информации Естественно, что выделение дискретных значений входного непрерывного сигнала приводит к потере части информации, содержащейся во входном сигнале. При этом, чем реже квантуется непрерывный сигнал тем большие потери информации при его прохождении через импульсный элемент. Условия для выбора частоты прерывания импульсного элемента определяются на основании теоремы Котельникова – Шеннона: Непрерывный сигнал с ограниченным частотным спектром в пределах от 0 до 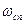полностью определяется последовательностью своих дискретных значений, если интервал прерывания выбран из условия 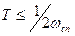(или частота прерывания из условия ).

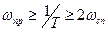Другими словами смысл теоремы заключается в том, что исходный непрерывный сигнал может быть восстановлен без искажения, если частота квантования в два раза или больше превышает предельную частоту в спектре непрерывного сигнала.

Здесь можно сказать, что в реальных системах вследствие фильтрующих свойств инерционных звеньев непрерывный сигнал обладает ограниченным спектром.

Классификация импульсных систем

В зависимости от типа ИЭ импульсные системы разделяются на: АИС; ШИС, ЧИС.

Эти ИС могут быть как разомкнутыми, так и замкнутыми и содержать в своем составе один или несколько ИЭ и непрерывную часть (НЧ).

а)

б)

В зависимости от того, соблюдается или не соблюдается принцип суперпозиции ИС подразделяются на линейные и нелинейные.

К линейным ИС относятся АИС с линейной характеристикой ИЭ и линейной частью НЧ.

К нелинейным ИС относятся ШИС и ЧИС, а также АИС с нелинейной характеристикой ИЭ или с нелинейной НЧ.

В настоящем разделе будет рассмотрена только теория линейных ИС.

Существуют также: а) синхронные (частный случай синфазные) и асинхронные ИС;

б) с постоянными и переменными параметрами и др. (см. Цыпкин Я.З. Теория Линейных Импульсных Систем).

Понятие о решетчатых функциях и разностных уравнениях

Поскольку выходной сигнал ИЭ определяется значениями входного сигнала только в определенные дискретные моменты времени, то в работе ИЭ ничего не изменится, если заменим непрерывную функцию на его входе дискретной функцией, значения которой в начале каждого периода совпадают со значениями непрерывной функции, а в остальное время равны нулю.

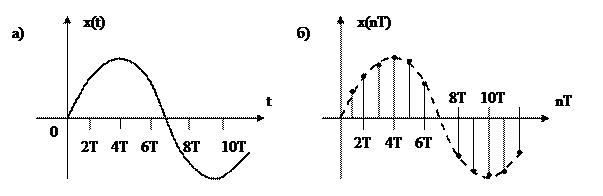
Рисунок 7.5

Такая функция дискретного аргумента называется решетчатой функцией (рисунок 7.5б.) и обозначается 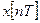. Непрерывная функция является огибающей для своей решетчатой функции .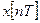

При рассмотрении дискретной функции удобно переходить к относительному времени 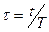. В этом случае непрерывной функции будет соответствовать решетчатая функция , где 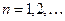, т.е. отсчет по шкале времени будет вестись в целочисленных единицах периода квантования .

Понятие решетчатой функции, лежащее в основе аппарата описания дискретных систем, позволяет осуществить переход к дискретному аналогу дифференциальных уравнений – разностным уравнениям.

Аналогами производных непрерывной функции для решетчатой функции являются разности. Первая разность (разность первого порядка) характеризует скорость изменения решетчатой функции и представляет собой аналог первой производной непрерывной функции:

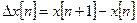(7.1)

Рисунок 76

Рисунок 7.6. Первая разность решетчатой функции .

Вторая разность (аналог второй производной)

. (7.2)

В общем, виде m – я разность

(7.3)

или, раскрывая значения разностей через значения решетчатой функции,

. (7.4)

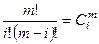– коэффициент бинома Ньютона. Аналогом интеграла для решетчатой функции является сумма .

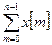Дифференциальные уравнения для решетчатых функций принимают форму разностных уравнений (уравнений в конечных разностях).

Стационарные линейные импульсные системы описываются линейным разностным уравнением с постоянными коэффициентами:

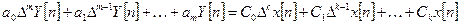. (7.5)

Учитывая связь значений разностей с дискретами решетчатой функции, разностное уравнение можно записать так:

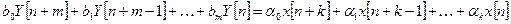. (7.6)

Для решения разностных уравнений широко применяются операционные методы, использующие различные преобразования.

Метод Z – преобразования

Как было рассмотрено в курсе ТЛСАР, использование преобразование Лапласа

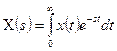(7.7)

облегчает анализ и синтез непрерывных САУ.

(7.8)

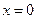при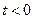

с – абсцисса абсолютной сходимости, которая выбирается так, чтобы удовлетворялось неравенство

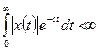(7.9)

Для большинства функций, с которыми приходится иметь дело в регулировании, абсцисса абсолютной сходимости равна нулю, т.е. . Поэтому для этих функций преобразование Лапласа переходит в преобразование Фурье после подстановки .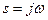

Задача анализа дискретных систем также может быть облегчена в результате применения подобного преобразования.

Если взять конечный интервал времени 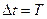( - заменим периодом квантования 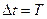) и представить текущее время в ви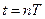де , где , то интеграл в выражении (7.7) можно заменить суммой:

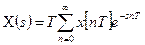. (7.10)

(7.10) – дискретное преобразование Лапласа.

Предел этого выражения при 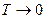даст преобразование Лапласа непрерывной величины (7.7).

Введем обозначение

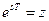. (7.11)

Тогда формулу (7.10) можно представить в следующем виде:

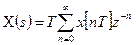. (7.12)

Второй сомножитель в правой части носит название – преобразования дискретной функции времени

. (7.13)

Выражение (7.13) является, по существу, деленным на преобразованием Лапласа дискретной функции времени при использовании подстановки (7.11).

Для нахождения оригинала или исходной решетчатой функции 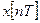по изображению 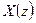используют формулу обратного – преобразования

(7.14)

причем интегрирование ведется по окружности:

, (7.15)

где с – абсцисса абсолютной сходимости.

Дискретное – преобразование имеет много сходных черт с непрерывным преобразованием Лапласа, например, в отношении линейности, сдвига во временной области и т.д.

С основными свойствами – преобразования ознакомиться самостоятельно.

Примеры определения – преобразований

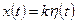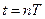1. Одиночный импульс при , где

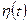- единичная импульсная функция;

- постоянный коэффициент,

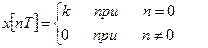(7.16)

Переходя к z – преобразованию решетчатой функции 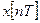и подставив в него значение 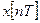из (7.16), получим

.

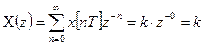2. Ступенчатая решетчатая функция 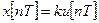, где

Подставим значение 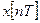в z – изображение :

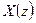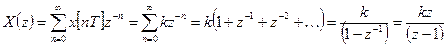, для .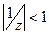

В учебных пособиях имеются таблицы z – преобразований наиболее часто используемых в САУ функций.

Передаточные функции импульсных систем

Введем понятие передаточной функции импульсного фильтра (рисунок 7.7), состоящего из импульсного элемента и непрерывной части.

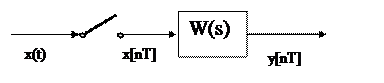
Рисунок 7.7

Для этого запишем вначале связь между входной и выходной величинами фильтра для изображений Лапласа:

, (7.18)

где изображение входной величины

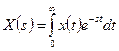
изображение выходной величины

и передаточная функция звена

.

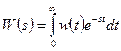Подставим эти значения в (7.18) и перейдем к конечному интервалу времени 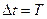. Тогда, положив 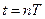и 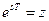, получаем

,

Отсюда, учитывая (7.13), находим

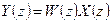. (7.19)

Здесь введена передаточная функция импульсного фильтра

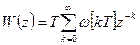(7.20)

чаще используется другое понятие передаточная функция импульсного фильтра

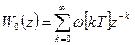(7.21)

В этом случае результирующая передаточная функция импульсного фильтра вместе с импульсным элементом будет

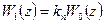, (7.22)

где 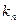- коэффициент передачи импульсного элемента.

Пример. Найдем передаточную функцию импульсного фильтра, представляющего собой идеальное интегрирующее звено с передаточной функцией

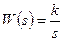
и импульсный элемент, генерирующий прямоугольные импульсы, продолжительность которых составляет 0,01T.

Функция веса и интегрирующего звена равна

По соответствующей таблице находим z – преобразование для этой функции, равное передаточной функции (7.21)

Найдем теперь передаточную функцию импульсного элемента. Площадь S генерируемого им прямоугольного импульса равна

,

где x – высота импульса (точнее величина на входе ИЭ).

.

Результирующая передаточная функция

.

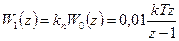Литература 1осн [406-427]; 2осн [212-243]; 4доп [571-593]; 5доп [47-68].

Контрольные вопросы

1 Какие виды квантования непрерывных сигналов Вы знаете?

2 Как подразделяют дискретные системы в зависимости от типа квантования?

3 Почему дискретные системы обладают большей помехозащищенностью по сравнению с аналоговыми?

4 Какие виды импульсной модуляции Вы знаете?

5 Из каких условий выбирается частота прерывания импульсного элемента?

6 Какие импульсные системы относятся к линейным, а какие к нелинейным?

7 Поясните понятия о решетчатых функциях и разностных уравнениях.

8 Что дает применение Z-преобразования при анализе импульсных систем?

Дата добавления: 2014-11-08