Лекция 4. Критерий абсолютной устойчивости В.М.Попова

Данный критерий, предложенный в 1960 г. румынским ученым В.М.Поповым, позволяет исследовать абсолютную устойчивость нелинейной системы с одной однозначной статической нелинейностью. Под абсолютной устойчивостью понимается устойчивость в целом при любой форме нелинейности, удовлетворяющей условиям

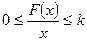при 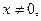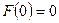. (4.1)

Рисунок 4.1

Про такие характеристики 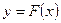(рисунок 4.1,а) говорят, что они лежат в угле 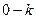, или принадлежит классу .

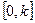Если равновесие системы (рисунок 4.1,б) абсолютно устойчиво, то оно абсолютно устойчиво и для всех прямолинейных характеристик , где , поскольку эти прямые также относятся к данному классу .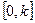

Рассмотрим случай, когда линейная часть устойчива и годограф вектора разомкнутой системы с линеаризованной характеристикой 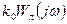не пересекает отрезка 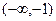или характеристика 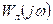не пересекала отрезок действительной оси. В соответствии с критерием Найквиста достаточно этого условия, чтобы замкнутая линейная система была устойчива. Так как , то достаточным условием устойчивости всех линейных систем, принадлежащих к классу 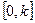, будет условие, чтобы 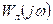не пересекала отрезка действительной оси .

Для произвольной нелинейной функции из класса 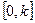достаточное условие абсолютной устойчивости было сформулировано В.М.Поповым. Приведем это условие без доказательства.

Для того, чтобы положение равновесия нелинейной системы с устойчивой линейной частью было устойчиво, достаточно выполнение следующих условий.

1. Существует такое вещественное число 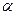, при котором вещественная часть функции Попова 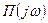будет положительна при всех :

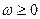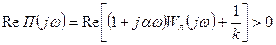. (4.2)

1. Функция принадлежит классу .

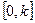Для практического применения критерия удобно использовать его геометрическое представление. Для этого предварительно введем видоизмененную частотную характеристику линейной части 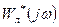, связанную с исходной 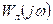следующими зависимостями:

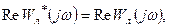
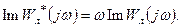(4.3)

Особенности видоизмененной характеристики: действительная ее часть равна действительной части исходной характеристики, мнимая равна мнимой части исходной, умноженной на 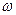(рисунок 4.2).

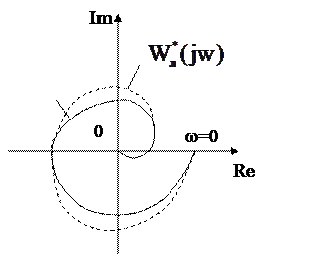
Рисунок 4.2

Теперь перейдем непосредственно к геометрической трактовке критерия В.М.Попова. на основании (4.2)

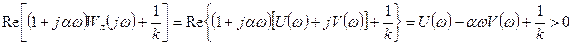
или

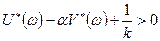(4.4)

при всех 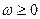. Это неравенство представляет собой другую формулировку критерия Попова.

При условии

(4.5)

получаем уравнение прямой на 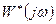. А прямая проходит через точку с координатами 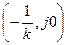с угловым коэффициентом, равным .

Отсюда вытекает графическая интерпретация критерия Попова: для установления устойчивости нелинейной системы достаточно подобрать такую прямую на плоскости 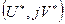, проходящую через тоску 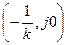, чтобы вся кривая 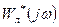лежала справа от этой прямой.

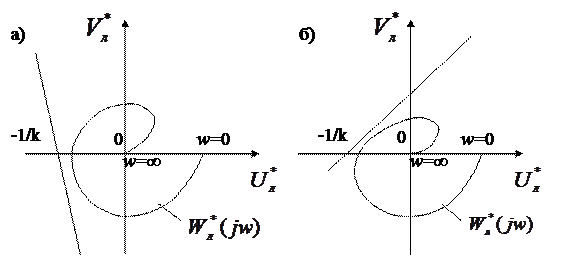
Рисунок 4.3

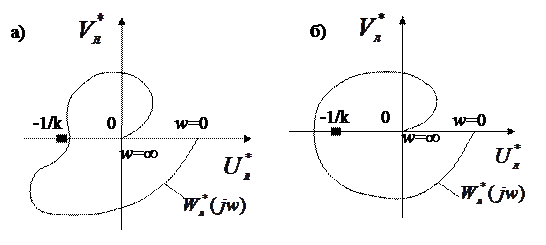
Рисунок 4.4

На рисунке (4.3,а, б) показаны случаи выполнения критерия, а на рисунке (4.4,а, б) – случаи, когда критерий Попова не выполняется.

Как показывает рисунок (4.4,а) достаточное условие устойчивости при произвольной форме однозначной нелинейной характеристики 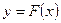в угле 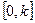оказывается строже необходимого и достаточного условия устойчивости в случае линейной характеристики в этом угле.

Критерий В.М.Попова распространен на системы с неустойчивой линейной частью:

Система абсолютна устойчива, если через точку 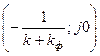можно провести прямую линию, проходящую слева от характеристики .

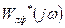Здесь 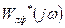- видоизмененная характеристика, исходной для которой является характеристика .

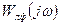Передаточная функция 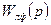связана с передаточной функцией 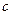следующим соотношением:

.

Здесь 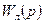– передаточная функция линейной части системы; 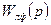– передаточная функция линейной части системы с дополнительной обратной связью 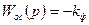, которая становится устойчивой за счет соответствующего выбора величины коэффициента передачи .

F_ф(x)

y

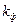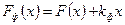
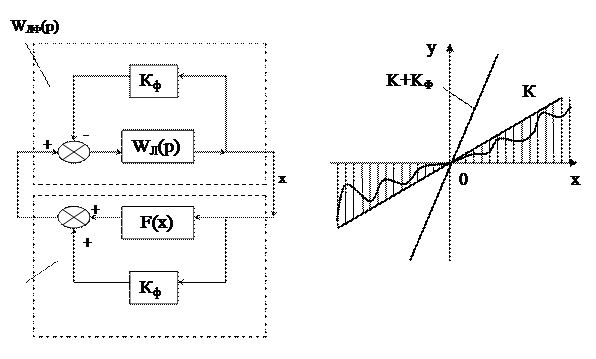
Рисунок 4.5

Достоинство критерия в его графической форме заключается в его применимости:

а) при любой сложности линейной части системы;

б) при наличии только экспериментально снятой характеристики линейной части 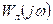, которую затем нетрудно перестроить в ;

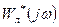в) при неизвестном очертании нелинейности и известных лишь пределах угла, в котором она располагается.

Литература 1осн [527-531]; 2осн [346-349]; 6доп [216-219].

Контрольные вопросы

1 Что понимается под абсолютной устойчивостью нелинейной системы?

2 Объяснить принадлежность однозначной статической нелинейности определенному классу.

3 Какие из критериев устойчивости лежит в основе критерия В.М. Попова?

4 Как строится так называемая видоизмененная частотная характеристика линейной части системы.

5 Графическая интерпретация критерия Попова?

6 Как можно распространить применение критерия Попова на системы с неустойчивой линейной частью?

7 Какие преимущества имеет применение критерия Попова в его графической форме?

Дата добавления: 2014-11-08