
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 8. Исследование устойчивости и качества импульсных САУ
|
|
|
|
Условия устойчивости линейных импульсных САУ
Как и в непрерывных системах, общее решение разностного уравнения импульсной системы
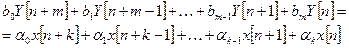 (8.1)
(8.1)
можно представить в виде суммы частного решения уравнения (8.1) с правой частью и общего решения уравнения без правой части:
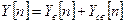 . (8.2)
. (8.2)
Составляющая 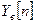 описывает вынужденное движение системы, а
описывает вынужденное движение системы, а  - переходное движение. Об устойчивости движения системы можно судить по состовляющей
- переходное движение. Об устойчивости движения системы можно судить по состовляющей  , определяемой из решения однородного разностного уравнения
, определяемой из решения однородного разностного уравнения
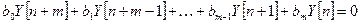 . (8.3)
. (8.3)
Общее решение этого уравнения при некратных корнях имеет вид
 , (8.4)
, (8.4)
где 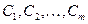 - постоянные коэффициенты, определяемые из начальных условий, а
- постоянные коэффициенты, определяемые из начальных условий, а 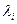 - корни характеристического уравнения
- корни характеристического уравнения
 . (8.5)
. (8.5)
Решение уравнения (8.4) определяет протекание переходного процесса в импульсной САУ (рисунок 8.1), т.е. дает отдельные значения регулируемой величины в моменты начала каждого периода чередования импульсов. Устойчивой будет такая САУ, в которой эти значения стремятся к нулю при неограниченном увеличении времени 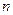 .
.
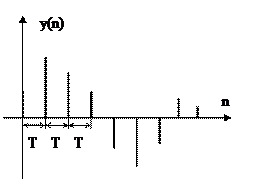 |
Рисунок 8.1
Как видно из (8.4) для устойчивости импульсной САУ необходимо и достаточно, чтобы корни характеристического уравнения (8.5) были по модулю меньше единицы.
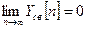 при
при 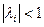
 . (8.6)
. (8.6)
Графически на комплексной плоскости корней 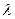 это соответствует расположению корней внутри круга единичного радиуса.
это соответствует расположению корней внутри круга единичного радиуса.

Рисунок 8.2
Рассмотрим импульсную САУ (рисунок 8.2). Пусть известна передаточная функция разомкнутой системы
 . (8.7)
. (8.7)
Передаточная функция замкнутой импульсной системы будет иметь вид
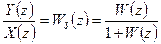 (8.8)
(8.8)
Передаточная функция по ошибке
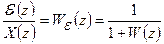 . (8.9)
. (8.9)
Здесь 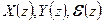 - z – преобразования входной величины, регулируемой величины и ошибки
- z – преобразования входной величины, регулируемой величины и ошибки 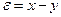 . Запишем характеристическое уравнение замкнутой системы
. Запишем характеристическое уравнение замкнутой системы
 (8.10)
(8.10)
Как было показано выше условием устойчивости линейной импульсной САУ будет ограничение по модулю корней характеристического уравнения
 . (8.11)
. (8.11)
Так например, для характеристического уравнения первого порядка
 (8.12)
(8.12)
Очевидное условие устойчивости будет  .
.
Аналогичным образом можно показать, что для уравнения второго порядка
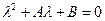 (8.13)
(8.13)
путем вычисления его корней получаются три условия устойчивости:
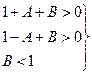 . (8.14)
. (8.14)
Нахождение корней характеристических уравнений высокого порядка связано с большим объемом вычислений. Поэтому для анализа импульсных систем применяются методы, позволяющие судить об устойчивости не вычисляя самих корней.
Критерии устойчивости линейных импульсных САУ.
Критерий Гурвица
Рассмотрим характеристический многочлен
 . (8.15)
. (8.15)
Критерий Гурвица позволяет оценивать расположение корней характеристического многочлена 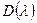 относительно мнимой оси плоскости комплексного переменного
относительно мнимой оси плоскости комплексного переменного 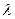 . Однако для исследования устойчивости импульсных систем требуется определить расположение корней характеристического многочлена относительно окружности единичного радиуса в плоскости комплексного переменного
. Однако для исследования устойчивости импульсных систем требуется определить расположение корней характеристического многочлена относительно окружности единичного радиуса в плоскости комплексного переменного 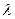 . Отсюда следует, что критерий Гурвица можно применить, если выполнить конформное отображение плоскости комплексного переменного
. Отсюда следует, что критерий Гурвица можно применить, если выполнить конформное отображение плоскости комплексного переменного 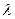 на плоскость комплексного переменного
на плоскость комплексного переменного 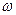 таким образом, чтобы единичная окружность
таким образом, чтобы единичная окружность  перешла в мнимую ось на плоскости переменного
перешла в мнимую ось на плоскости переменного 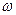 , а внутренность единичного круга
, а внутренность единичного круга  отобразилась на левую полуплоскость
отобразилась на левую полуплоскость  (рисунок 8.3).
(рисунок 8.3).
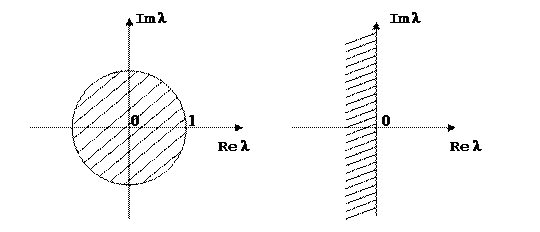
Рисунок 8.3
Такое отображение выполняется с помощью дробно – линейного преобразования
 , (8.16)
, (8.16)
или
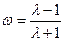 .
.
Выполняя замену переменной в многочлене 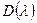 , получим
, получим
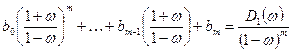 , (8.17)
, (8.17)
где 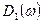 - многочлен степени
- многочлен степени 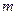 от новой переменной
от новой переменной 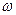 :
:
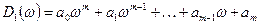 . (8.18)
. (8.18)
Например, при  получим
получим
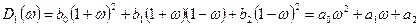 ,
,
где
 (8.19)
(8.19)
В результате проведенного 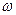 - преобразования корни
- преобразования корни 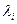 , лежащие внутри единичной окружности, переходят в корни
, лежащие внутри единичной окружности, переходят в корни 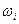 , лежащие в левой полуплоскости. Теперь для исследования корней характеристического многочлена (8.18) применим критерий Гурвица. Для этого составим определитель Гурвица:
, лежащие в левой полуплоскости. Теперь для исследования корней характеристического многочлена (8.18) применим критерий Гурвица. Для этого составим определитель Гурвица:
 . (8.20)
. (8.20)
Согласно теореме Гурвица, для того чтобы все корни многочлена 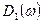 имели отрицательные вещественные части, необходимо и достаточно, чтобы все диагональные миноры определителя (8.20) были положительны:
имели отрицательные вещественные части, необходимо и достаточно, чтобы все диагональные миноры определителя (8.20) были положительны:
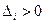
 . (8.21)
. (8.21)
При этом, как показано выше, все корни  характеристического многочлена
характеристического многочлена 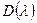 лежат строго внутри круга единичного радиуса:
лежат строго внутри круга единичного радиуса:
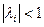
 .
.
Пример. Дано  .
.
Перейдем к переменной 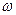 в соответствии с формулой (16):
в соответствии с формулой (16):
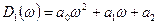 ,
,
где 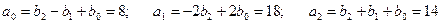 .
.
Тогда 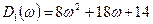 .
.
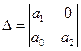
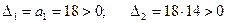 .
.
Следовательно, все корни многочлена 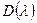 лежат внутри единичного круга.
лежат внутри единичного круга.
Недостатком рассмотренного подхода к анализу устойчивости является необходимость выполнения 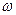 - преобразования. В ряде случаев более удобно исследовать непосредственно, характеристическое уравнение (или годограф АФЧХ) импульсных систем.
- преобразования. В ряде случаев более удобно исследовать непосредственно, характеристическое уравнение (или годограф АФЧХ) импульсных систем.
Алгебраический критерий Шур – Кона
Пусть характеристическое уравнение замкнутой импульсной системы имеет вид
 (8.22)
(8.22)
или
 . (8.23)
. (8.23)
Рассмотрим следующую последовательность определителей, составленных из коэффициентов характеристического уравнения (8.23)

где

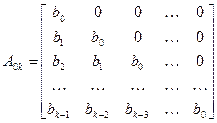 ,
, 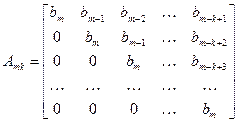 .
.
Если 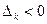 при
при  нечетном,
нечетном, 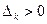 при
при  четном корни характеристического уравнения (8.23) лежат внутри единичного круга.
четном корни характеристического уравнения (8.23) лежат внутри единичного круга.
Например, определитель первого порядка при 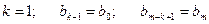 равен
равен
 .
.
Определитель второго порядка при  равен
равен
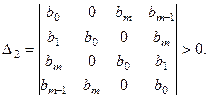
Определитель третьего порядка при 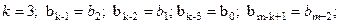
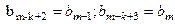 равен
равен
 .
.
Пример. Определить устойчивость импульсной системы, характеристическое уравнение которой
 .
.
Составим определители:


Так как 
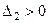 , то система устойчива. Действительно, корни характеристического уравнения
, то система устойчива. Действительно, корни характеристического уравнения 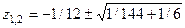 ;
; 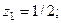
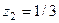 , т.е. по модулю не превышают 1.
, т.е. по модулю не превышают 1.
Дискретный аналог критерия Михайлова
Пусть характеристическое уравнение импульсной системы имеет вид
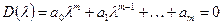 . (8.24)
. (8.24)
Это уравнение при известных корнях 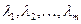 можно записать
можно записать
 . (8.25)
. (8.25)
Пусть  и
и 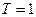 , тогда (8.25) будет иметь вид
, тогда (8.25) будет иметь вид
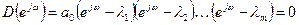 . (8.26)
. (8.26)
Очевидно, что результирующий угол поворота вектора 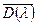 при изменении
при изменении 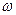 от
от  до
до  будет равен сумме углов поворота отдельных векторов – сомножителей
будет равен сумме углов поворота отдельных векторов – сомножителей 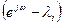 , где
, где  .
.
Для устойчивой системы все корни 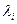 расположены внутри круга единичного радиуса, описываемого концом вектора
расположены внутри круга единичного радиуса, описываемого концом вектора 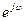 при изменении
при изменении 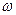 от
от  до
до  .
.
Часть корней неустойчивой системы расположены вне единичного круга.
Рассмотрим оба этих случая для одного из сомножителей 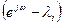 .
.
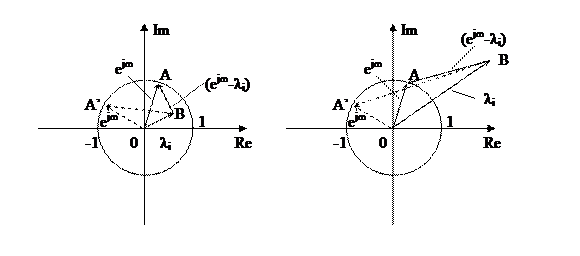
Рисунок 8.1 Рисунок 8.2
Пусть 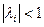 (рисунок 8.1). При изменении
(рисунок 8.1). При изменении 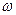 в пределах
в пределах  конец вектора
конец вектора  описывает окружность единичного радиуса. Конец вектора
описывает окружность единичного радиуса. Конец вектора  находится внутри единичного круга. Поэтому угол поворота суммарного вектора
находится внутри единичного круга. Поэтому угол поворота суммарного вектора 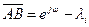 равен
равен  . Следовательно, каждый корень
. Следовательно, каждый корень 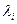 характеристического уравнения, находящийся внутри единичного круга, обеспечивает приращение суммарному вектору
характеристического уравнения, находящийся внутри единичного круга, обеспечивает приращение суммарному вектору  , равное
, равное  . Поэтому общий угол поворота вектора
. Поэтому общий угол поворота вектора 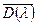 равен
равен 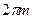 .
.
Пусть теперь 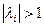 (рисунок 8.2). Конец вектора
(рисунок 8.2). Конец вектора  находится за пределами единичного круга. При изменении
находится за пределами единичного круга. При изменении 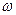 от
от  до
до  суммарный вектор
суммарный вектор 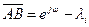 повернется на одинаковые углы в положительном и отрицательном направлениях, а результирующий угол поворота будет равен 0. Следовательно, корни
повернется на одинаковые углы в положительном и отрицательном направлениях, а результирующий угол поворота будет равен 0. Следовательно, корни 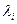 , расположенные вне единичного круга, не будет давать приращения к углу поворота вектора
, расположенные вне единичного круга, не будет давать приращения к углу поворота вектора 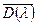 и общий угол поворота его будет меньше, чем
и общий угол поворота его будет меньше, чем 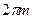 .
.
Формулировка критерия: Для устойчивости замкнутой импульсной системы необходимо и достаточно, чтобы вектор 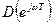 при изменении
при изменении 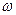 от
от  до
до  (при
(при 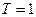 ), монотонно возрастая и не обращаясь в нуль, вращался против часовой стрелки, при этом результирующий угол поворота вектора должен равняться
), монотонно возрастая и не обращаясь в нуль, вращался против часовой стрелки, при этом результирующий угол поворота вектора должен равняться 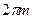 , где
, где 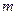 - степень характеристического уравнения системы.
- степень характеристического уравнения системы.
Дискретный аналог критерия Найквиста
Позволяет исследовать устойчивость замкнутой импульсной системы на основе анализа дискретной передаточной функции разомкнутой системы.
Пусть задана передаточная функция разомкнутой импульсной системы
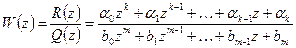 . (8.27)
. (8.27)
Передаточная функция замкнутой системы:
 (8.28)
(8.28)
Рассмотрим вспомогательную функцию вида
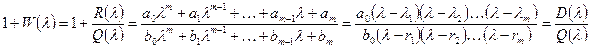 , (8.29)
, (8.29)
где 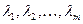 – нули выражения (8.29), т.е. корни многочлена
– нули выражения (8.29), т.е. корни многочлена 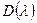 ;
; 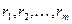 - полюсы выражения (8.29), т.е. корни многочлена
- полюсы выражения (8.29), т.е. корни многочлена 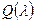 .
.
В формальной записи сказанное выглядит следующим образом:
Пусть  и
и 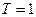 , тогда
, тогда
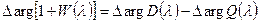 . (8.30)
. (8.30)
Согласно принципа аргумента: 1) если замкнутая система устойчива и все 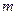 корней лежат внутри единичного круга, то
корней лежат внутри единичного круга, то  ; 2) если разомкнутая система неустойчива и только часть полюсов равная
; 2) если разомкнутая система неустойчива и только часть полюсов равная 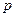 лежит внутри единичного круга, то
лежит внутри единичного круга, то 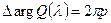 .
.
Тогда
 , (8.31)
, (8.31)
где 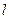 - число полюсов, расположенных вне единичного круга.
- число полюсов, расположенных вне единичного круга.
Выражение (8,31) является условием устойчивости замкнутой импульсной системы.
Полагая 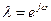 , перепишем это условие в окончательном виде:
, перепишем это условие в окончательном виде:
 . (8.32)
. (8.32)
Поскольку годограф вектора 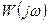 симметричен относительно вещественной оси, то достаточно построить только половину этого годографа и применить полученное условие устойчивости при
симметричен относительно вещественной оси, то достаточно построить только половину этого годографа и применить полученное условие устойчивости при 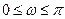 .
.
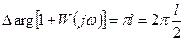 . (8.33)
. (8.33)
Переходя от вспомогательной функции  к годографу АФЧХ разомкнутой импульсной системы
к годографу АФЧХ разомкнутой импульсной системы 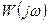 , можно сформулировать условие устойчивости (8.33) следующим образом:
, можно сформулировать условие устойчивости (8.33) следующим образом:
Для того чтобы замкнутая импульсная система была устойчива, необходимо и достаточно чтобы годограф 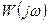 при изменении переменной
при изменении переменной 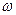 в пределах от 0 до
в пределах от 0 до  обходил точку
обходил точку  последовательно в положительном направлении
последовательно в положительном направлении 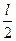 раз, где
раз, где 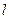 - число полюсов передаточной функции разомкнутой системы
- число полюсов передаточной функции разомкнутой системы  , расположенных вне круга единичного радиуса.
, расположенных вне круга единичного радиуса.
Если, в частности, разомкнутая система устойчива, то 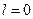 . В этом случае: Замкнутая система устойчива, если годограф
. В этом случае: Замкнутая система устойчива, если годограф 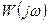 не охватывает точку
не охватывает точку  при изменении
при изменении 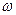 от 0 до
от 0 до  .
.
Примеры годографов 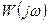 устойчивых систем при различных значениях числа
устойчивых систем при различных значениях числа 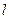 приведены на рисунке 8.3.
приведены на рисунке 8.3.
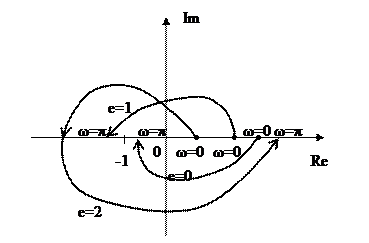
Рисунок 8.3
В случае нейтральной разомкнутой части критерий формулируется так же как и в случае устойчивой разомкнутой системы, но только для годографа вектора 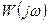 , дополненного дугой бесконечного радиуса, начинающейся на действительной оси. Поскольку характеристика
, дополненного дугой бесконечного радиуса, начинающейся на действительной оси. Поскольку характеристика 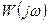 при
при 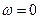 начинается в бесконечности (рисунок 8.4).
начинается в бесконечности (рисунок 8.4).

Рисунок 8.4
На рисунке 8.4,б годографы соответствуют устойчивой импульсной системе.
Аналог критерия Найквиста весьма удобен при исследовании устойчивости импульсных систем с известными или экспериментально снятыми частотными характеристиками.
Анализ качества импульсных систем
Качественные показатели характеризуют точность и быстродействие системы. Оценки качества регулирования подразделяют на прямые и косвенные. Прямые оценки качества определяют непосредственно по кривой переходного процесса, а косвенные – расчетным путем.
Анализ точности импульсных САУ
Установившаяся точность импульсной системы может оцениваться при помощи коэффициентов ошибок.
В непрерывных системах при подаче на вход сигнала 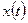 ошибку
ошибку 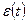 определяют как
определяют как
 , (8.34)
, (8.34)
где  - весовая функция (для сигнала ошибки).
- весовая функция (для сигнала ошибки).
В импульсных системах величина ошибки в дискретные моменты  может быть получена из (8.34) при переходе от интеграла к сумме и замене
может быть получена из (8.34) при переходе от интеграла к сумме и замене 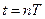 ,
, 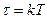 ,
,  на
на 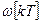 , т.е..
, т.е..
 . (8.35)
. (8.35)
Разложение в ряд Тейлора функции  имеет следующий вид:
имеет следующий вид:
 . (8.36)
. (8.36)
Величину ошибки 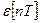 определяет из
определяет из
 , (8.37)
, (8.37)
где коэффициенты ошибки:
 .
.
Суммарные оценки качества
Косвенными оценками качества регулирования импульсной системы, учитывающими не только длительность процесса, но и его форму, могут служить дискретные аналоги интегральных оценок – суммарные оценки.
Простейшая суммарная оценка имеет вид
 . (8.38)
. (8.38)
Такую оценку используют в случае монотонных переходных процессов (рис. 8.5).

Рисунок 8.5
Линейная суммарная оценка равна заштрихованной площади ступенчатой функции (рисунок 8.5).
В случае колебательных процессов используют квадратичную суммарную оценку
 . (8.39)
. (8.39)
Формулы для вычисления этой оценки через коэффициенты разностного уравнения, описывающего, динамику импульсной системы имеются в литературе [1доп].
Коррекция импульсных систем
Задача, решаемая на этапе коррекции, состоит в определении КУ, обеспечивающих достаточно хорошее приближение частотных характеристик синтезированной системы к желаемым частотным характеристикам.
В отличии от непрерывных САУ в импульсных системах применяют два способа коррекции – непрерывный и импульсный.
Непрерывная коррекция. В непрерывной разомкнутой САУ при введении последовательного КУ общая передаточная функция имеет следующий вид:
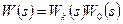 (8.40)
(8.40)
При изменении параметров КУ общая передаточная функция также изменяется и характеристики замкнутой системы можно скорректировать в желаемом направлении.
Наличие процессов прерывания в импульсных САУ обусловливает определенные особенности последовательной коррекции.
Пусть дискретная передаточная функция некорректированной системы равна 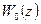 . При введении последовательного КУ передаточная функция разомкнутой системы имеет вид
. При введении последовательного КУ передаточная функция разомкнутой системы имеет вид
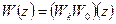 , (8.41)
, (8.41)
и
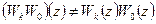 . (8.42)
. (8.42)
Следовательно, дискретная передаточная функция скорректированной разомкнутой системы не является простым произведением передаточной функции составляющих звеньев, поскольку результат распространения процесса прерывания через отдельные звенья 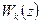 и
и 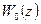 не эквивалентен результату распространения такого процесса последовательную цепь из
не эквивалентен результату распространения такого процесса последовательную цепь из 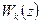 и
и 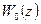 .
.
Приближенное представление дискретной части системы в виде непрерывного звена все же позволяет использовать обычные приемы последовательной коррекции, рассмотренные в осеннем семестре.
Импульсная коррекция. Осуществляется включением в контур системы импульсного фильтра. Наиболее простым способом коррекции является введение последовательной цепи в виде ИЭ и НЧ.
Передаточная функция разомкнутой системы будет иметь следующий вид:
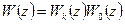 (8.43)
(8.43)
Метод коррекции в этом случае не отличается от метода последовательной коррекции непрерывных систем. Передаточную функцию КУ легко получить путем сравнения частотных характеристик желаемой системы с характеристиками некорректированной системы.
Литература 1осн [430-441]; [449-473]; 3осн [93-105]; 5доп [69-84]; 6доп [239-245].
Контрольные вопросы
1 Необходимые и достаточные условия устойчивости линейных импульсных систем.
2 Можно ли использовать критерий Гурвица для анализа устойчивости линейной импульсной системы?
3 Когда удобнее использовать алгебраический критерий Шур-Кона?
4 Дайте геометрическую интерпретацию дискретного аналога критерия Михайлова.
5 Дайте формулировки дискретного аналога критерия Найквиста, если: а) разомкнутая система неустойчива; б) разомкнутая система устойчива или нейтральна.
6 Какие Вы знаете косвенные методы оценки качества линейных импульсных систем?
7 Какие Вы знаете способы коррекции импульсных систем?
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 2189; Нарушение авторских прав?; Мы поможем в написании вашей работы!