Извлечение корня из комплексных чисел

Пусть n – натуральное число. Корнем n – степени из комплексного числа 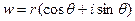называется комплексное число 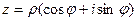, для которого .

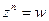Обозначим его

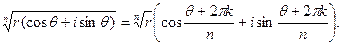
Давая k значения 0,1,2,…,(n-1)? Получим n различных значений корня. Для значений k=n,n+1… или k=-1, -2,…

и т.д. значения корней будут повторять полученные ранее значения.

Например, при k=0 имеем . При k=n имеем и т.д.

Обобщая данный частный случай, можно сказать, что геометрически точки, соответствующие различным значениям корня n – й степени из комплексного числа 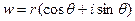, располагаются в вершинах правильного n – угольника с центром θ, причем одна из вершин соответствует числу .

Действительная часть комплексного числа обозначается ReZ (ReZ=x), а мнимая часть обозначается символом ImZ (ImZ=y). Следовательно, комплексное число можно записать .

Запись комплексного числа 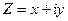называется алгебраической формой записи.

Комплексное число называется сопряженным с комплексным числом 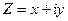и обозначается .

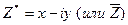Каждое комплексное число 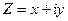можно изобразить на плоскости Оху в виде точки M(x,y) или ее радиус – вектором 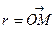и обратно, всякая точка M(x,y) плоскости Оху может быть рассмотрена как геометрический образ комплексного числа .

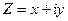Таким образом, комплексные числа могут изображаться как точками, так и векторами. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох — действительная ось, ось Оу — мнимая. Модуль числа Z равен расстоянию точки М(х,у), изображающей это число, от начала координат. Введя полярную систему координат, получим 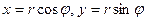, тогда 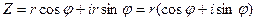. Выражение называется тригонометрической формой записи комплексного числа Z. Величины r и φвыражаются через х и у (см. рис. 4).

Рис. 4.

и называются соответственно модулем и аргументом комплексного числа 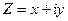. Аргумент φкомплексного числа Z определяется неоднозначно, а с точностью до слагаемого 2πk, где k— любое целое число.

Значение argZ, удовлетворяющее условию 0 называется главным значением аргумента и обозначается символом argZ. В некоторых случаях главным значением аргумента называют значение argZ, удовлетворяющее условию 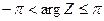. Если r = 0, то комплексное число равно нулю и его аргумент неопределён. Действительное число имеет аргумент 2πk (главное значение аргумента равно нулю), если оно положительное, и 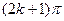(главное значение аргумента равно π^-), если оно отрицательное. Если действительная часть комплексного числа равна нулю

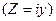— называется чисто мнимым комплексным числом), то аргумент его равен (главное значение аргумента равно 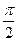, если у > 0 и или 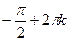; (главное значение аргумента равно 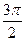или ), если у < 0. Аргумент комплексного числа, угол φ, считается положительным, если он отсчитывается от положительного направления оси Ох против часовой стрелки, и отрицательным при противоположном направлении отсчёта.

Пример. Записать в тригонометрической форме следующие комплексные числа:

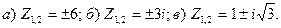
Решение. Для того, чтобы комплексное число 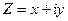записать в тригонометрической форме, нужно найти его модуль и значение аргумента φ, который связан с координатами х и у следующими формулами , причём ни одна из этих формул в отдельности не позволяет найти φпо заданным х и у.

а) Любое действительное число а можно записать в тригонометрической форме.

1. а > 0, 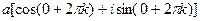и, если ограничиться главным значением аргумента (k = 0), то .

2. a < 0, 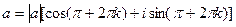и, если ограничиться главным значением аргумента (k = 0), то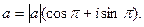

Тогда:

и при k=0,

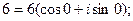
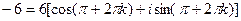и при k=0.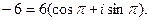

б) Z = 3i. Так как в этом случае действительная часть равна нулю, то комплексное число находится на оси Оу и r = |3|, а аргумент его равен , если у>0 и

при у < 0. Тогда:

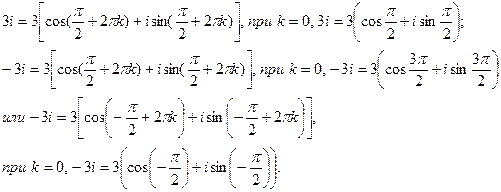
в) 1. 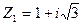. Так как то 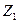лежит в первой координатной четверти, а соответствует . Другой способ. Так как 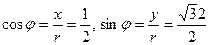, то φ находится в первой координатной четверти и равен . Следовательно

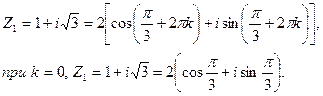
2. . 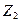лежит в четвертой четверти (x>0, y<0) и , тогда 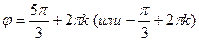или так как , то φ находится в четвертой координатной четверти и равен 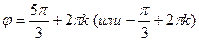. Тогда

Для того, чтобы записать комплексное число 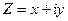в показательной форме , используем формулы Эйлера

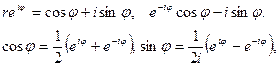
выражающие показательную функцию через тригонометрическую и обратно. Тогда получим

Используя формулы Эйлера, можно выразить любую целую положительную степень cosx и sinx, а также их произведения в виде суммы членов, содержащих лишь первые степени синусы и косинусы кратных дуг:

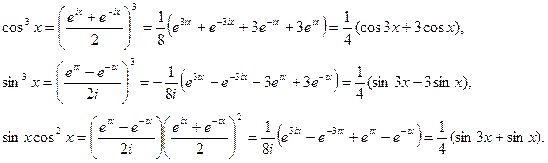
Пример. Представить в комплексной форме следующее число:

Решение. Ограничимся главными значениями аргументов.

Пример. Найти значения: и решить уравнения

Решение. Так как

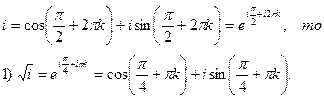
Полагая k=0 и k=1, находим два значения корня

При дальнейших значения k корни будут повторятся.

3) Учитывая, что 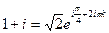, получим

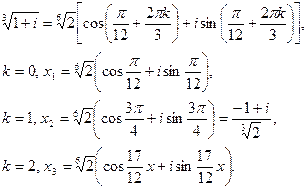
При дальнейших значения k корни будут повторятся.

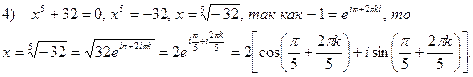
Дата добавления: 2014-11-08