Теоремы о пределах

1. Функция имеет не более одного предела. Пусть y=f(x) имеет два предела при х→а: .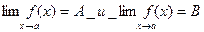

По теореме (1) f(x)=A+α(x), где α(x)→0.

(2) f(x)=B+β(x), где β(x)→0.

Рассмотрим (1) – (2) 0=А+ α(x)-В- β(x) следовательно В – А = α(x) - β(x), т.к. α(x) - β(x) – есть бесконечно малая функция при х→а, а В – А – число не равное нулю, по условию, то быть равными они не могут, значит наше предположение не верно. Функция имеет не более одного предела.

2. Предел алгебраической суммы двух функций при и х→а, равен алгебраической сумме пределов этих функций при х→а.

;

3. Предел произведения двух функций имеющих конечный предел при х→а, равен произведению пределов этих функций при х→а.

.

4. Предел от постоянной функции при х→а равен значению этих функций. у=с. 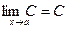. С – константа.

5. Постоянный множитель можно выносить за знак предела.

6. Предел частного двух функций при х→а, равен частному пределов этих функций при х→а, если предел делителя не равен нулю, т.е.

.

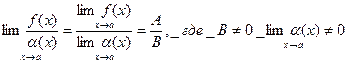7. Если сложная функция y=f(u),

, то предел сложной функции .

Сравнение бесконечно малых величин.

Пусть α(x); β(x);γ(x) – функции бесконечно малые при х→а. (а – число или ∞; +∞; - ∞). Бесконечно малые функции часто сравниваются по быстроте стремления к нулю. Рассмотрим бесконечно малые величины

Если мы сравним друг с другом более далекие значения наших бесконечно малых величин, то заметим, что они приближаются к нулю с разными скоростями.

.

Ясно, что быстрее, чем ,а быстрее, чем .

Определение. Если предел отношения 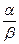при х→а равен нулю, то говорят, что α – бесконечно малая более высокого порядка, чем β.

Определение. Если предел отношения 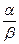при х→а конечен и отличен от нуля, то α и β называются бесконечно малыми одного порядка малости.

Определение. Если предел отношения 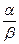при х→а равен ∞, то говорят, что α(х) бесконечно малая низшего порядка малости, по сравнению с β(х)

Чтобы сравнить две бесконечно малые величины необходимо найти предел их отношения.

Не всякие бесконечно малые величины можно сравнить между собой.

- не существует.

Если предела отношения двух бесконечно малых величин не существует, то говорят, что эти бесконечно малые величины не сравнимы.

Определение. Две бесконечно малые величины называются эквивалентными, если предел их отношения равен 1.

- эквивалентные бесконечно малые величины.

Теорема. При раскрытии неопределенности вида можно и числитель и знаменатель этой неопределенности заменить величинами им эквивалентными.

Два замечательных предела.

Лемма. Если , то справедливо неравенство 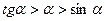(ά в радианах).

Теорема. Предел отношения синуса бесконечно малого угла к величине этого угла в радианах равен 1.

.

2) Второй замечательный предел.

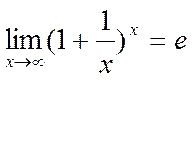
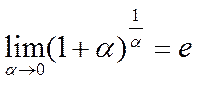
Дата добавления: 2014-11-08