Сложные процентные ставки

Сложные проценты

Наращение по сложным процентам

Сложными называются ставки процентов, которые применяются к сумме с начисленными в предыдущем периоде процентами. Основное отличие сложных процентов от простых заключается в том, что база для начисления процентов меняется от одного расчётного периода к другому. Механизм наращения первоначального капитала по сложным процентам называется капитализацией процентов.

Сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга.

Существуют два способа начисления сложных процентов: антисипативный и декурсивный. Рассмотрим декурсивный метод расчёта сложных процентов. В этом случае начисление процентов на первоначальную сумму производится в конце периода наращения. В конце первого периода (года) наращенная сумма равна:

S = P (1+ i).

В конце второго периода (года) проценты начисляются на уже наращенную сумму

S = P (1+ i)(1+ i)= P (1+ i)²,

и так далее. В конце n -ого периода (года) наращенная сумма будет равна

S=P (1+ i) ⁿ. (1.11)

Формула (1.11) называется формулой наращения по сложным процентам (формулой сложных процентов). Множитель (1+ i) ⁿ в формуле (1.11) является коэффициентом наращения.

Формулы удвоения суммы

В целях оценки своих перспектив кредитору и должнику интересно знать, через сколько лет сумма ссуды возрастёт в N раз при данной процентной ставке. Для этого приравняем коэффициент наращения величине N, в результате получим:

а) для простых процентов 1+ ni = N, тогда

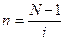; (1.12)

б) для сложных процентов (1+ i) ⁿ = N, тогда

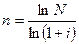. (1.13)

Для случая N= 2 формулы (1.12) и (1.13) называются формулами удвоения и принимают следующий вид:

а) для простых процентов

n= 1/ i; (1.14)

б) для сложных процентов

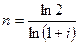. (1.15)

При небольших ставках процентов (менее 10%) вместо формулы (1.22) можно использовать приближённую формулу, если учесть, что ln 2»0,7, а ln(1+ i)» i. Тогда

n» 0,7/ i. (1.16)

□ Пример 1.5. За сколько лет долг увеличится вдвое при ставке простых и сложных процентов, равной 5%?

Решение.

1. Случай простых процентов:

n= 1/0,05=20 лет.

2. Случай сложных процентов, вычисленных по точной формуле:

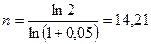лет.

3. Случай сложных процентов, вычисленных по приближённой формуле:

n»0,7/0,05=14 лет.

Таким образом, одинаковое значение ставок простых и сложных процентов приводит к различным результатам, при малых значениях ставки сложных процентов точная и приближённая формулы дают практически одинаковые результаты.■

Начисление сложных процентов при дробном числе лет

Если срок ссуды измеряется дробным числом лет, то наращенную сумму можно найти различными способами:

1. по формуле сложных процентов

S=P (1+ i) ⁿ,

2. смешанным методом, согласно которому за целое число лет начисляются сложные проценты, а за дробное — простые

S=P (1+ i)^{[ n ]}(1+{ n } i), (1.17)

где [ n ] — целая часть числа n; { n } — дробная часть числа n.

3. в ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т. е.

S=P (1+ i)^{[ n ]}. (1.18)

Номинальная ставка

В контрактах на получение кредитов часто предусматривается капитализация процентов по полугодиям, кварталам, иногда помесячно. Пусть годовая ставка сложных процентов равна j, а число периодов начисления в году m. Тогда каждый раз проценты начисляются по ставке j/m. Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по формуле

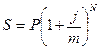, (1.19)

где N=mn — число периодов начисления, n — число лет.

Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена несколькими способами, приводящими к различным результатам:

1. по формуле сложных процентов

, (1.20)

где N/t — число периодов начисления процентов, t — период начисления процентов;

2. по смешанному методу

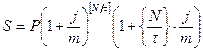, (1.21)

где [ N/t ] — число полных периодов начисления процентов, { N/t } — дробная часть одного периода начисления процентов.

□ Пример 1.6. На сумму 600 ден. ед. ежеквартально по ставке 12% годовых начисляются сложные проценты в течение 14 месяцев. Определите величину наращенной суммы двумя методами.

Решение. Общее число периодов начисления процентов составит , т. е. 4 квартала и 2 месяца. По формуле сложных процентов наращенная сумма будет равна

ден. ед.

Используя смешанный метод начисления, наращенная сумма составит:

ден. ед.

Если дробную часть не учитывать, то наращенная сумма будет равна:

ден. ед.

Из полученных результатов расчёта следует, что для ссудодателя выгоднее смешанный метод начисления процентов, т. к. итоговая сумма получается максимальной, а для заёмщика предпочтительнее третий вариант, т. к. итоговая сумма минимальна. ■

Переменные ставки сложных процентов

Нестабильность экономической ситуации вынуждает банки использовать в кредитных сделках изменяющиеся во времени, но заранее фиксированные для каждого периода ставки сложных процентов. В этом случае наращенная сумма может быть определена по формуле:

, (1.22)

где P — первоначальная сумма; i_t — ставка простых процентов в периоде с номером ; n_t — продолжительность периода начисления по ставке i_t.

1.2.2 Сложные учётные ставки

Наращение по сложной учётной ставке

Принцип начисления сложных антисипативных процентов аналогичен методу начисления простых антисипативных процентов. В первом периоде наращенная сумма определяется по формуле

,

во втором периоде она будет равна

,

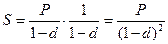и так далее, в n -ом периоде

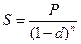, (1.23)

где d — учётная ставка сложных процентов; n — число лет. Формула (1.23) называется формулой наращения по сложным антисипативным процентам (формулой сложных антисипативных процентов). Множитель 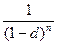в формуле (1.23) является коэффициентом наращения.

Номинальная учётная ставка процентов

В тех случаях, когда начисление сложных антисипативных процентов производят m раз в году, используют номинальную учётную ставку f. Тогда каждый раз проценты начисляются по ставке f/m, и наращенная сумма определяется по формуле

, (1.24)

где, N=mn — число периодов начисления, n — число лет.

□ Пример 1.7. Срочный вклад в размере 800 ден. ед. положен в банк на 2,5 года. По условиям договора начисления процентов производится один раз в году по сложной учётной ставке d =15% годовых. Определить наращенную сумму.

Решение. Наращенная сумма составит

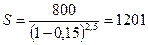ден. ед.

Если наращение по учётной ставке производить не один, а два раза в год (m =2), то наращенная сумма будет равна:

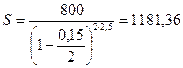ден. ед. ■

Дата добавления: 2014-11-25