Погашение потребительского кредита изменяющимися суммами

Другой регулярной схемой погашения в потребительском кредите является метод ускоренной амортизации процентов. Основной долг, как и в равномерном случае, погашается равными долями, тогда как процентные платежи представляют собой убывающую арифметическую прогрессию.

Наращенная сумма долга определяется по формуле

S=P (1+ ni), (5.3)

а сумма разового погасительного платежа q будет зависеть от числа погасительных платежей в году (m). Разовый погасительный платёж будет равен

, k =1, 2, …, nm, (5.4)

где

и

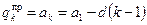, d >0.

Уравнение баланса в этом случае имеет вид:

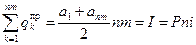. (5.5)

Задавая один из параметров прогрессии, например a ₁ или d, можно найти все остальные процентные платежи. Чаще всего определяются не сами платежи 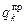, а их веса

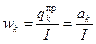, (5.6)

т. е. доля платежа в общей сумме процентов. Тогда сумма всех весов равна 1:

; w_nm=w ₁–(nm– 1) d.

В этих двух уравнениях из трёх величин =w ₁, w_nm, d одну можно выбрать произвольно. Так, для годового кредита, погашаемого 12 ежемесячными платежами, при условии, что процентная часть уменьшается с каждым платежом на 1/12, т. е. 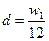, получаем

,

откуда

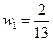и .

Таким образом

; , , …,

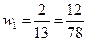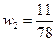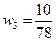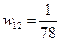
и из формулы (5.6) получаем размер процентных платежей:

; …, .

Рассмотренная схема называется «правилом 78». Это правило получило такое название потому, что сумма порядковых номеров месяцев года 78 (1+2+....+12=78). В соответствии с этим правилом уплата процентов при первом платеже составит величину 12/78 общей начисленной суммы процентов, а оставшаяся часть платежа пойдёт на уплату основного долга. При втором платеже на оплату процентов пойдет 11/78 общей начисленной суммы процентов и т. д.

□ Пример 5.2. Кредит в сумме 10 тыс. ден. ед. выдан на 6 месяцев под 20% годовых (проценты простые). Погашение задолженности производится ежемесячными платежами. Составить план погашения задолженности.

Решение. Наращенная сумма долга в конце периода составит:

S = P (1+ ni)=10×(1+0,5 × 0,2)=11 тыс. ден. ед.

Сумма начисленных процентов

I = Pni =10 × 0,5 × 0,2=1 тыс. ден. ед.

Ежемесячные выплаты

q = S/ 6=11/6=1,83333 тыс. ден. ед.

Найдём сумму порядковых номеров месяцев

1+2+3+4+5+6=21

Из первого платежа в счёт уплаты процентов идёт 6/21 общей суммы начисленных процентов

тыс. ден. ед.

Сумма, идущая на погашение основного долга, составляет

1,83333–0,28571=1,54762 тыс. ден. ед.

Из второго платежа в счёт уплаты процентов идёт 5/21 общей суммы начисленных процентов.

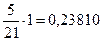тыс. ден. ед.

Сумма, идущая на погашение долга, составляет

1,83333–0,23810=1,59523 тыс. ден. ед.

и так далее.

Все вычисления запишем в таблицу.

План погашения долга.

■

Дата добавления: 2014-11-25