Алыпты таралу 3 страница

Анализдің абсолютті қатесін 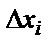деп белгілейді, оны мына теңдеумен анықтайды:

,

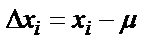бұндағы, 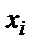– анализ нәтижесі, 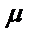– анализденетін компоненттің сынамадағы ақиқат мөлшері.

Абсолютті қатенің өлшенетін ақиқат мәнге қатынасын анализдің салыстырмалы қатесі дейді.

Әдетте салыстырмалы қатені пайызбен, кейде бірлік үлесімен де көрсетеді:

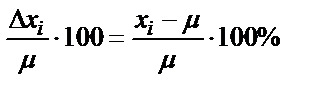
Анализденетін компоненттің сынамадағы ақиқат мәні анализ нәтижесінде қатенің болуына байланысты белгісіз болып қалады. Тәжірибеде есептеу барысында ақиқат мәннің орнына шын мәнінде болатын мәнді қолданады, ол бірнеше параллельді анықтаулардың орташа арифметикалық мәніне тең болады.

Өлшеу қатесі көптеген факторларға байланысты болады: қолданылатын құрылғылардың қандай дәлдік класына жататындығына, өлшеу әдістемесіне, байқаушының индиви­дуальды (жеке) қабілеті мен ерекшеліктеріне және т.б.

2.4.1. Жүйелі қателер

Анализдің қайталап өлшегенде тұрақты болып қалатын немесе белгілі бір заңдылыққа сәйкес өзгеретін қатесін систематикалық (жүйелі) қате деп атайды.

Жүйелі қатенің таңбасы бір тәжірибеден екіншіге ауысқанда өзгермейді. Жүйелі қате нәтижені тек қана төмендетеді немесе тек қана жоғарлатады.

Жүйелі қателердің пайда болу себептері мен олардың көздері алуан түрлі болады. Байқалу сипатына байланысты жүйелі қатені бірнеше түрге бөлуге болады – тұрақты, про­грессивті (қарқынды) және басқалары. Жиі кездесетін түрі – тұрақты жүйелі қателер, олардың мәндері ұзақ уақыт бойы сақталады.

Прогрессивті (қарқынды) қателер үздіксіз өседі немесе кемиді. Пайда болу себептеріне байланысты жүйелі қателерді инструментальды қате, әдістің қатесі, субъективті қате және т.б. деп бөледі.

Инструментальды (аспаптық немесе құралдық) қате анализ барысында әртүрлі құралдар мен құрылғыларды қолданумен байланысты болады. Аналитикалық тәжірибеде қолданылатын құралдар мен құрылғылар дәлдіктің белгілі бір класымен сипатталады, көп жағдайда инструментальды қатені дәлдігі жоғары класқа сәйкес келетін құрал не құрылғыны қолданып төмендетуге болады. Инструментальды қатенің көзі ретінде дәлденбеген салмағы әртүрлі гирлерді, калибрленбеген өлшем ыдыстарын, спектрофотометрдің призмасының қозғалуын, фотоэлементте қараңғылаушы токтың пайда болуын және т.б. айтуға болады. Көбінесе бұндай қателерді калибрлеу кезінде немесе құрылғының көрсетулерін басқа дәлдігі жоғары құрылғының нәтижесімен салыстыру арқылы алынған түзету крэффициенттерін енгізіп мейлінше төмендетуге болады.

Құрылғылардың тозуы, ескіруі және істен шығуы әдетте сырт көзге байқалмайды, сондықтан олардың жұмысқа қабілеттігін белгілі деңгейде ұстап тұру үшін оларды тексеруден өткізеді және градуирлейді. Құралдар мен құрылғыларды тексеруден өткізу заңды түрде және метрологиялық қызмет орындарының қатысуымен іске асырылуы тиіс.

Әдістің қатесі анализденетін жүйенің қасиетіне, яғни тұндыру немесе жуу кезіндегі тұнбаның ерігіштігіне, қосарлана­тұнуға, фотометрленетін ерітінділердің уақыт бойынша тұрақсыздығына, реакцияның толық жүрмеуіне және т.б. байланысты болады.

Сонымен қатар анықталатын компонентке кедергі әсер ететін қоспасы бар реактивті қолдануда жүйелі қатені тудырады. Реактивті алдын ала жақсылап тазарту жүйелі қатені нөлге дейін төмендетуге және жоюға мүмкіндік береді. Әдістемелік қателер көп жағдайда байқалмай қалады. Оперативті және жеке, немесе субъективті қателердің маңызы зор, өйткені олар анализ барысында орындалатын операциялармен, әсіресе аналитиктің квалификациясымен және оның жеке қабілеттерімен байланысты. Мысалы, аналитиктің титрлеу кезіндегі индикаторлар түсінің ауысуын дәл анықтай білуі өте маңызды.

Әдетте, жүйелі қатені дер кезінде табу және оны ескеру міндетті. Жүйелі қатені табудың практикада кең тараған тәсілі анализді тәуелсіз әдіспен орындау, яғни бос тәжірибе жасау және стандартты үлгілер анализін орындау.

Бос тәжірибе кезінде көбінесе алынған нәтиже жүйелі қатені көрсетеді немесе дұрыс нәтиже алу үшін оның мәнін сынаманың аналитикалық сигналының мәнінен шегеріп тастайды.

Жүйелі қатені табудың қолайлы және жиі қолданылатын тәсілі стандартты үлгілер анализінің нәтижесін стандартты үлгінің паспорттағы мәндерімен салыстыру болып табылады. Стандартты үлгілер – бұлар әртүрлі материалдар, анықталатын элементтің олардың құрамындағы мөлшері жоғары дәрежелі дәлдікпен белгілі болады. Оларды әртүрлі аналитикалық әдістерде градуирленген графиктер тұрғызу үшін, анализдің дұрыстығын бақылау үшін және әртүрлі анализ әдістерінің объективті метрологиялық сипаттамаларын алу үшін және т.б. қолданады.

Стандартты үлгілерге белгілі талаптар қойылады. Олардың ішіндегі маңыздысы мыналар: эталондалған элементтер ақиқат мәннен өзгеше болмауы тиіс, стандартты үлгілердің паспорттары болуы тиіс, ұзақ уақыт сақтағаннан олардың құрамдары өзгермеуі тиіс, химиялық құрамы біркелкі және сынамаға сәйкес болуы тиіс.

Қара және түсті металдардың сенімді эталондары болады. Ал рудалар, минералдар, тау жыныстары және т.б. бойынша эталон дайындау мейлінше қиын, бұл олардың құрамдарының біркелкі болмауымен түсіндіріледі.

2.3-кесте

Жүйелі қателерді топтастыру

Түрі	Сипаттамасы	Себебі	Жою әдісі
I	Табиғаты белгі­лі, мәні белгілі немесе оларды есептеуге бола­ды.	Айқын емес заңдылық­тардың байқалмай қалуы. Мысалдар: 1) температураның концентрацияға әсері; 2) индикаторлық қателер және т.б.	Түзету шамасын есептеу және кіргізу.
II	Табиғаты белгі­сіз, мәндері де белгісіз.	Әр түрлі: 1) Аспаптық: а) өлшеуіш ыдыстарды қолданғанда; б) салмақты өлшеген­де; в) өлшеудің дәл болмауы; г) сигналдың дұрыс өңделмеуі; 2) реактивтік – реактивтер тазалығы­ның қанағаттанар­лықтай болмауы; 3) әдістемелік: әр алуан себептерден (реакцияның толық өтпеуі, тұнбаның то­лық бөлінбеуі, қосар­лана тұну, ұшқыш қосы­лыстардың түзілуі және т.б.)	1) Эксперимент қою арқылы неме­се анализ жасалып жатқанда: а) өлшеуіш ыдыс­тардың көлемін тексеру; б) таразыны салыс­тырып тексеру; таразы гирлерін эталон­мен салыстыру; в) түрлі аспап­тарды өзара салыс­тырып тексеру; г) математикалық әдістерді қолдану. 2) Бақылау тә­жіри­­белері мен бос тәжірибелер өткізу. 3) Әр әдістеме үшін өзіндік ерек­шелігі болады.
II	Табиғаты анықталмаған, мәні белгісіз (Курье моделінің Ғ (p) қатесі кіреді)	Әр түрлі: 1) ыдыстан былғану; 2) температураның әсері; 3) уақыт әсері; 4) ылғалдың әсері; 5) жұмыс реті; 6) бөліп алу кезінде физика-химиялық процестердің бұзылуы; 7) анализденген объектінің өзіндік ерекшеліктері; 8) оперативтік, жеке бастылық және т.б.	Барлық операцияларды біртіндеп қайта қарастыру, реактивтерді, ыдыстарды, химик-аналитикті және т.б. алмастыру.

2.4.2. Кездейсоқ қателер

Кездейсоқ қателердің белгілі бір таңбасы болмайды, «кездейсоқ» деп аталуының өзі оның пайда болуында қандай да бір заңдылықтың байқалмайтынын көрсетеді. Кездейсоқ қателердің болуы параллельді жүргізілген анализдерде жүйелі қателерді болдырмау шараларын ескеріп, түзету коэффициенттерін қолданғанның өзінде де анализ нәтижелерінің бір-бірінен өзгеше болуымен түсіндіріледі. Кездейсоқ қателерді әдетте кездейсоқ құбылыс ретінде қарастырады және бұл қателерді ықтималдылық теориясы мен математикалық статистиканың негізінде өңдейді.

Анализдің қайталап өлшегенде кездейсоқ, яғни кенеттен пайда болған қатесін кездейсоқ қате деп атайды.

Кездейсоқ мәннің таңбасы өлшеулер сериясында тұрақты болып қалмайды және тәжірибеден тәжірибеге ауысқанда өзгереді.

Берілген жағдайда болжанған мәннен әлдеқайда өзгеше болатын өрескел қатені ағаттықтар (секірмелі мәндер) деп атайды.

Ағаттықтар (секірмелі мәндер) – бұлар үлкен ауытқулар, анализдің көзге түсетін жаңсақтықтары, көбінесе олақтықтан, салақтықтан, дұрыс көңіл бөлмеуден немесе білімнің жетіспеу­шілігінен, аналитиктің жеке басының құзіретсіздігінен, кездей­соқтықтардың сәтсіз тоғысуынан туындайды. Олар әдетте аналитиктің дөрекі оперативті қателер жіберуінен болады, мысалы сүзу, құрыштау немесе өлшеу кезінде тұнбаның белгілі мөлшерін шашып алуы, яғни оның массасын жоғалтуы және т.б. Үйреншікті мысал ретінде студенттердің тамшуырды (пипет­каны) дұрыс пайдаланбауын келтіруге болады. Ағаттықтар анализ нәтижесін бұрмалағандықтан, оларды анықтап алады және көбінесе есептен шығарып тастайды.

2.5. Анализ нәтижелерінің дұрыстығы, жинақтылығы, қайталанымдылығы, дәлдігі, орта мән және стандартты ауытқу

Дұрыстық – анализ өлшеулерінің сапасы, олардың нәтиже­леріндегі жүйелі қатенің нөлге жақындығын бейнелейді. Дұрыстықтың сандық бағалануы ретінде D = 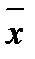– х_ақиқ есептеледі, немесе, жеке нәтиже үшін:

D = х_і – х_ақиқ

х_ақиқ (ақиқат мән) дегеніміз, «қайсы-бір шаманы сапалық және сандық жағынан мүлтіксіз сипаттайтын мән». Шартты ақиқат мән дегеніміз, «өлшенетін шаманың эксперименттік жолмен алынған және ақиқат мәнге соншалықты жақын болғандықтан, алға қойылған өлшеу мақсатында ақиқат мән орнына қолданыла алатын нақты мәні».

Өлшеу нәтижелерінің жинақтылығы (ұқсастығы) дегеніміз – бірдей жағдайда (бір ғана аналитиктің орындауында, бір ғана аспаптың, реактивтің, матрицаның, ортаның көмегімен ғана, уақыттың аз аралығында) жасалған өлшеулер нәтижелерінің бір-біріне жақындығын көрсететін өлшеу сапасы.

Өлшеулердің қайталанымдылығы дегеніміз – әртүрлі жағдайда (әртүрлі уақытта, әртүрлі орындарда, әртүрлі әдістер мен құралдардардың көмегімен) орындалған өлшеулердің нәтижелерінің бір-біріне жақындығын көрсететін өлшеулер сапасы.

Өлшеулердің дәлдігі деп өлшеулер нәтижелерінің анық­талатын шамасының ақиқат мәніне жақындығын көрсететін өлшеулердің сапасын айтады. Дәлдік жоғары болса, оған сәйкес қате де, яғни жүйелік қатеде, кездейсоқ қатеде аз болады. Дәлдік термині, әдетте, жалпылаушы термин ретінде қолданылады, ол жүйелі қателердің жойылуын немесе есепке алынуын және кездейсоқ қателердің азаюын бейнелейді: неғұрлым жалпы қате аз болса, соғұрлым дәлдік жоғары болады.

Анализдің компоненттің ақиқат мәніне өте жақын болатын және оны алмастыра алатын нәтижесін шынайы дәл мөлшер деп атайды.

Өлшелінген шаманың математикалық статистика бойынша неғұрлым дұрыс және мейлінше мүмкін болатын (ықтимал) мәнін оның математикалық күтімі береді. Математикалық күтім n дискретті өлшемдер сериясы үшін мына теңдеумен өлшенеді:

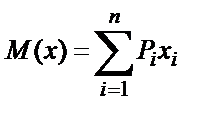(2.1)

бұндағы, x_{i –} i - ші өлшеу нәтижесі; P_i – оның ықтималдығы.

Тең нүктелік (дәлдігі бірдей) өлшемдер жағдайында

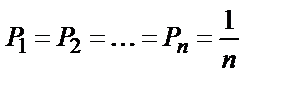
және (2.1) мынадай теңдікке көшеді:

.

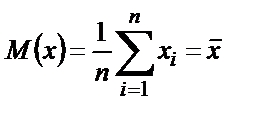Демек тең нүктелік өлшемдер кезінде математикалық күту арифметикалық орташа ұғымымен сәйкес келеді.

x_i мәндерінің арифметикалық орташа шамадан 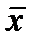ауытқулары квадраттарының қосындысы, x_i мәндерінің кез келген басқа шамадан ауытқулары квадраттарының қосындысынан кіші болады, яғни мына шексіздік орындалады:

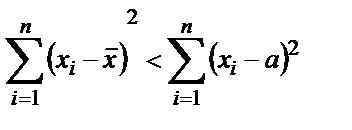
бұндағы a≠ .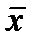

Орташа арифметикалық шама мен математикалық болжамның бір-бірімен сәйкес келуі гипотетикалық бас жиынтыққа жатады, яғни осы жағдайдағы мүмкін болатын өлшемдер жиынтығын құрайды. Осы өлшемдердің арифме­тикалық орта мәні басты орташа мән деп аталады. Аналитикалық химияда параллельді анықтаулар әдетте көп болмайды және алынған нәтижелердің жиынтығы таңдалған жиынтық немесе кездейсоқ жиынтық деп, ал кездейсоқ таңдалған нәтиженің орташа мәні – таңдалған орташа деп аталады.

Кездейсоқ таңдау кезінде өлшемдер санының өзгеруінен орташа арифметикалық шаманың өзгеруі де мүмкін екендігі белгілі. Бірақ ол математикалық болжамнан көп өзгере қоймайды, соған жуық болады. Таңдау көлемі кең болған сайын орташа арифметикалық шаманың мәні математикалық болжамға жақындай түседі.

Статистикалық анализ әдісі бойынша кездейсоқ таңдаулар нәтижесіне сүйене отырып, бас жиынтық параметрін бағалауға және сол арқылы сынамадағы компоненттің мейлінше ықтималды мәнін табуға болады.

Егер сынамадағы компонентті бір әдіспен параллельді анықтаулар нәтижесі x₁,x₂, …,x_n – болса, онда олардың орташа арифметикалық мәні мынаған тең болады:

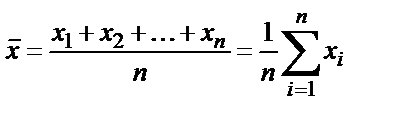(2.2)

Мысалы, қалайының қоладағы мөлшерін оның тиомочевинамен комплексі түрінде фотометриялық әдіспен төрт параллельді анықтау бойынша нәтижесі мынадай болса (ω_Sn%):4,80; 4,65; 4,84; 4,61. (2.2) теңдеуіне сәйкес арифметикалық орташаның мәні төмендегідей болады:

.

Есептеу қолайлы болу үшін әдетте санақтың бастамасын мүмкін болатын мәнге ығыстырады және есептеуде мына теңдеуді қолданады:

,

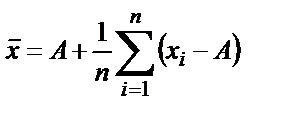бұндағы А – еркін таңдалған мән, санақтың бастамасы осы мәнге ығыстырылады.

Мысал үшін А= 4,60 тең деп алып, 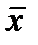есептейміз:

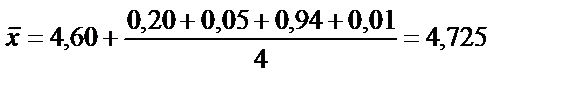
Геометриялық орташа мән арифметикалық мәннен төмен болады. Бұл тәсіл дөңгелектеуге байланысты пайда болатын қатені болдырмау мақсатында қолданылады. Кейбір жағдайларда студенттер компьютер немесе микрокалькулятор­лар көмегімен есептеу барысында үтірден кейінгі сандарды түгел жазып алады. Алайда олай істеуге болмайды. Өйткені үтірден кейінгі сандар анализдің дәлдігін сипаттамайды. Орташа мәнді есептеу барысында және аралық есептеулерде үтірден кейін бастапқыда слынған нәтижелерден бір ғана таңбаға артық болатын сандарды ескерген дұрыс. Соңғы нәтижені ғана дөңгелектеп алуға болады. Дөңгелектеуді арнайы ережеге сәйкес жүзеге асырады.

Анализдің жекелеген нәтижелері x₁, x₂,,..., x_і x_min - нан x_max – ға дейінгі белгілі бір аралығына таралады.

Бұл аралықты рұқсат етілген айырмашылық (құлаш – R) деп атайды. Рұқсат етілген айырмышылық та аналитикалық бақылаудың немесе оның сатыларының дұрыстығын тексеруге арналған негізгі метрологиялық сипаттамалардың қатарына жатады.

Жеке нәтиже мен орташа мәннің арасындағы айырма­шылықты кездейсоқ ауытқу немесе жеке ауытқу не болмаса жәй ауытқу d деп атайды:

.

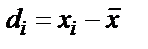Кездейсоқ шаманың орташа мәнмен салыстырғандағы таралуы дисперсиямен 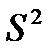сипатталады:

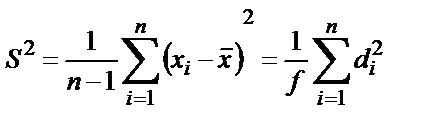(2.3)

бұндағы f=n-1 бос дәреже саны, ол тәуелсіз өлшеулер санымен анықталады.

Дисперсияның қателер теориясы үшін маңызды қасиеттерінің бірін мына теңдеу көрсетеді:

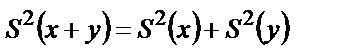, (2.4)

яғни, кездейсоқ шамалардың дисперсиясы олардың әрқайсысының дисперсиясының қосындысына тең болады. Бұл, айталық, кездейсоқ шамалардың қосындысындағы қателерді есептегенде олардың дисперсиясын ескерген дұрыс деген сөз.

Алайда нәтижелердің таралуының сандық сипаттамалары үшін дисперсияны қолдану мүмкін емес, өйткені олардың өлшемдері анализ нәтижесінің өлшемдерімен сәйкес келмейді. Таралуды сипаттау үшін стандартты ауытқуды қолданады:

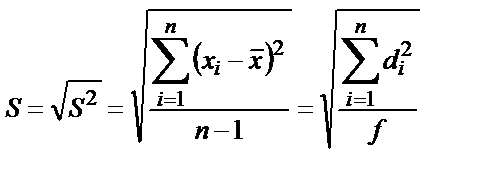. (2.5)

Бұл мәнді орташа квадраттық (немесе квадраттық) ауытқу немесе жеке нәтиженің орташа квадраттық қатесі деп атайды. Оны мына теңдеумен есептеуге болады:

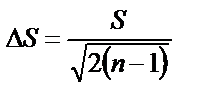. (2.6)

Осылайша, анализ нәтижесін өңдеу кезінде әдетте басты орташаны μ -ді емес, орташа таңдамалыны 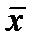, таңдамалы стандартты ауытқуды емес таңдамалы дисперсияны, σ² –ты емес басты жинақтылықты сипаттайтын σ –ны анықтайды. Дегенмен кездейсоқ таңдаулардың нәтижесі басты жинақтылықтың параметрін анықтауға мүмкіндік береді.

Қайталанымдылықты бағалау үшін орта мәннің таңдамалы дисперсиясын

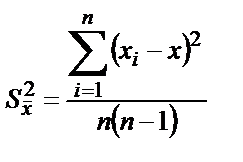(2.7)

және стандартты ауытқуды немесе орташа нәтиженің орташа квадратты қатесін есептейді:

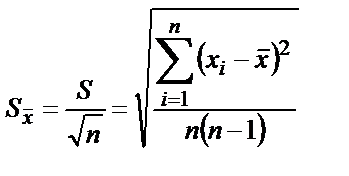(2.8)

2.5 – теңдеуіндегі квадраттар қосындысын былайша түрлен­діруге болады:

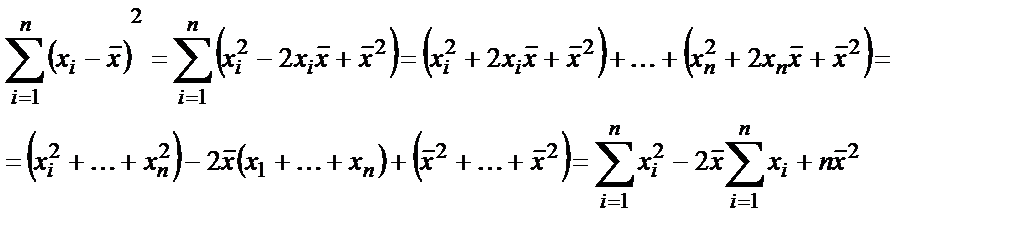
Осыған 2.2 қатынасын қойсақ, онда:

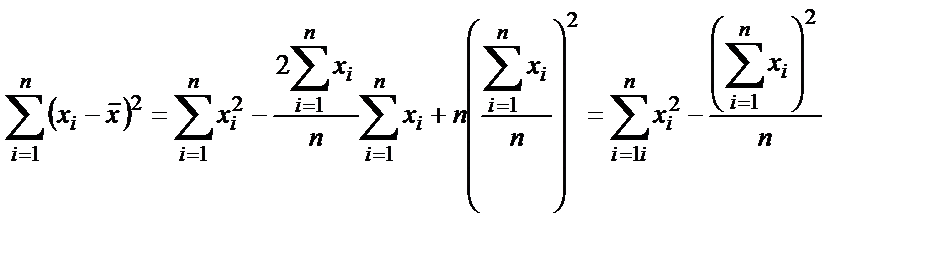. (2.9)

Немесе қысқартып жазсақ:

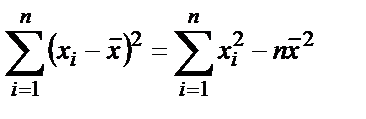(2.10)

2.10 – теңдігі қарапайым және алғашында практикалық есептеулер үшін қолайлы сияқты көрінеді. Алайда бұл теңдеу бойынша есептегенде екі үлкен мәннің арасындағы айырмашылық аз сияқты көрінеді де, сөйтіп анализдің дәлдігі бұрмаланады. Бұл әсіресе қарапайым дөңгелектеу жолымен алынған таңбасы бірнеше санға қысқарған 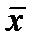мәндерін қолданғанда байқалады. 2.9 теңдеуінде дөңгелектенетін мәндер жоқ, сондықтан екі үлкен мәннің арасындағы айырмашылық эффектісі оншалықты байқалмайды. Сондықтан да практикалық есептеулерде 2.9 теңдеуін қолданған тиімді болады. Бұл кезде дисперсияны есептеуге арналған теңдік мынадай түрге ие болады

(2.11)

және стандартты ауытқуды келесі теңдеумен есептеуге болады:

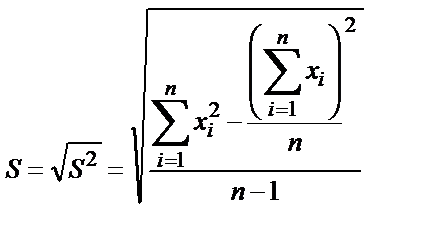(2.12)

Орташа мәнді, дисперсияны және орташа нәтиженің стандартты ауытқуын есептесек (құйманың құрамындағы Pb-ды анықтағандағы (%)): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,49.

2.3 – теңдігі бойынша А=14,50 болғанда

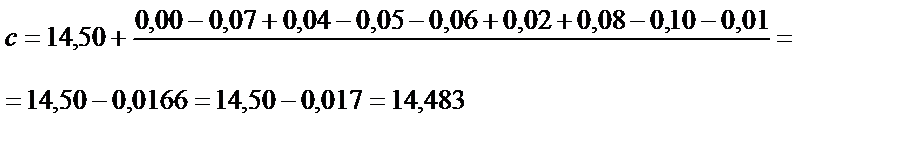
2.5 – теңдігіне сәйкес дисперсия мынаған тең болады:

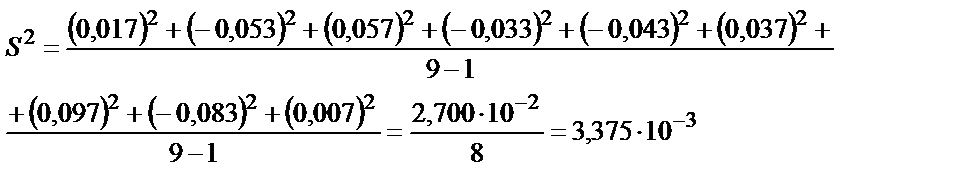
2.11 – теңдігі бойынша S² – сандық мәні мынаған тең:

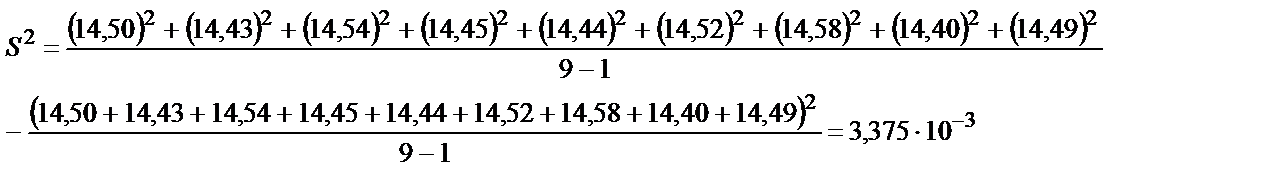
Бұл бұған дейін есептелген нәтижелермен сәйкес келеді және квадратты алмай тұрып, ( 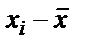) табуды қажет етпейді.

2.10 – теңдеуін қолданғанда S² орташа арифметикалық мәні дөңгелектеуге байланысты өзгереді:

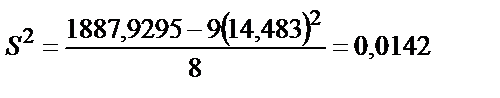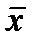; ( =14,483 болғанда);

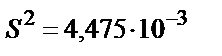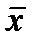( =14,4833 болғанда);

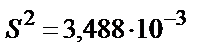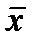( =14,48333 болғанда);

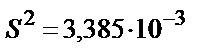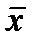( =14,483333 болғанда).

Келтірілген нәтижелерден дисперсияның осы жағдайдағы шынайы мәні тек орташа арифметикалық мәнді, яғни үтірден кейін 6 санды алғанда ғана дұрыс болатынын көруге болады, сондықтан 2.10 теңдігін қолданып жүргізілетін есептеулерге қарағанда 2.9 теңдігін қолданған дұрыс сияқты. Стандартты ауытқуды (квадраттық қатені) 2.5 – теңдігі арқылы есептейді:

Дата добавления: 2014-11-25