
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тест тапсырмалары. Қосындының немесе айырымның орташа квадраттық қателерін мынадай теңдеумен есептеуге болады:
|
|
|
|
.
.
.
Қосындының немесе айырымның орташа квадраттық қателерін мынадай теңдеумен есептеуге болады:
Көбейтіндінің немесе бөлшектің қателері салыстырмалы қатенің димсперсиясы бойыншада есептеледі:
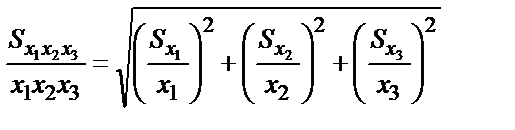 (2.17)
(2.17)
2.9. Өрескел қатені табу
Кейбір жағдайларда бірнеше параллельді анықтаулардың арасынан олардан мүлдем өзгеше және орташа арифметикалық мәннен де өзгеше болатын анализ нәтижесі байқалады. «Тым» жоғары немесе «тым» төмен нәтижені жай алып тастау анализ нәтижесін кәдімгідей орташа арифметикалық мәнді есептеуге қате мәлімет қосқан сияқты бұрмалауы мүмкін. Сондықтан өрескел қатені есептеу өте маңызды нәрсе. Өрескел қатені есептеу үшін анықтаулар саны өте көп болмағанда критерийін  қолданады:
қолданады:
 , (2.18)
, (2.18)
бұндағы x1 – сенімсіздік тудырған және ерекшеленген мән; x2 – оған көрші мән; R – мәндердің ауытқуы, қарастырылып отырған қатардағы максимальды және минимальды x мәндерінің айырымы.
(2.18) теңдеуі бойынша есептелген  –ды оның кестедегі берілген ықтималдық пен бос дәреже санындағы мәнімен Qкесте салыстырады. Бұндай мәндерді 2.5-кестесінен алуға болады. Егер
–ды оның кестедегі берілген ықтималдық пен бос дәреже санындағы мәнімен Qкесте салыстырады. Бұндай мәндерді 2.5-кестесінен алуға болады. Егер 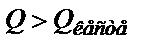 болса, онда сенімсіздік тудырған мән өрескел қате болғаны және оны орташа арифметикалық мәнді есепетегенде қолданбау керек.
болса, онда сенімсіздік тудырған мән өрескел қате болғаны және оны орташа арифметикалық мәнді есепетегенде қолданбау керек.
2.5-кесте
Qкесте – нің сандық мәндері
| f | P | f | P | ||||
| 0,90 | 0,95 | 0,99 | 0,90 | 0,95 | 0,99 | ||
| 0,89 | 0,94 | 0,99 | 0,43 | 0,51 | 0,64 | ||
| 0,68 | 0,77 | 0,89 | 0,40 | 0,48 | 0,58 | ||
| 0,56 | 0,64 | 0,76 | 0,37 | 0,46 | 0,53 | ||
| 0,48 | 0,56 | 0,70 | 0,34 | 0,44 | 0,48 |
Ал егерде 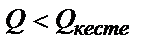 болса, онда ол мән өрескел қате болып есептелмейді. Мысалы, қоланың құрамындағы қалайыны анықтағанда анализдің 5,10% Sn бар нәтижесі сенімсіздік тудырған, оның
болса, онда ол мән өрескел қате болып есептелмейді. Мысалы, қоланың құрамындағы қалайыны анықтағанда анализдің 5,10% Sn бар нәтижесі сенімсіздік тудырған, оның 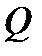 критерийі:
критерийі:

Ал Qкесте –нің Р=0,95 және f=4 болғандағы мәні 0,64. Яғни 5,10% Sn бар нәтиже өрескел қате емес.
Күмән келтіретін жағдайларда және (2.18) теңдеуі бойынша есептелген 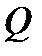 –нің мәні Qкесте –ге жақын мән болса, онда стандартты ауытқуды есептеу арқылы өрескел қатенің бар жоғын анықтауға болады. Егер
–нің мәні Qкесте –ге жақын мән болса, онда стандартты ауытқуды есептеу арқылы өрескел қатенің бар жоғын анықтауға болады. Егер
 (2.20)
(2.20)
немесе
 (2.21)
(2.21)
болса, онда сенімсіздік тудыратын x1 мәні өрескел қате болғаны. (2.20) теңдеуіндегі 3 коэффициентін кейде 4-ке ауыстырады.
Сонымен қатар Vmax қатынасын есептеуге негізделген әдісте бар:
 (2.22)
(2.22)
Егер (2.22) теңдеуі бойынша есептелген Vmax мәні оның кестелік мәнінен жоғары болса, онда x1 нәтижесі өрескел қате болғаны, сондықтан оны орташа мәнді есептегенде және одан басқа да есептеулерде қолданбаған дұрыс.
2.6-кесте
α мәнділік деңгейіндегі және n өлшемдер қатарындағы Vmax мәндері
| n | a | n | a | ||||||
| 0,1 | 0,05 | 0,025 | 0,01 | 0,1 | 0,05 | 0,025 | 0,01 | ||
| 1,41 | 1,41 | 1,41 | 1,41 | 2,23 | 2,39 | 2,52 | 2,66 | ||
| 1,65 | 1,69 | 1,71 | 1,72 | 2,26 | 2,43 | 2,56 | 2,71 | ||
| 1,79 | 1,87 | 1,92 | 1,96 | 2,30 | 2,46 | 2,60 | 2,73 | ||
| 1,89 | 2,00 | 2,07 | 2,13 | 2,33 | 2,49 | 2,64 | 2,80 | ||
| 1,97 | 2,09 | 2,18 | 2,27 | 2,35 | 2,52 | 2,67 | 2,84 | ||
| 2,04 | 2,17 | 2,27 | 2,37 | 2,38 | 2,55 | 2,70 | 2,87 | ||
| 2,10 | 2,24 | 2,35 | 2,46 | 2,40 | 2,58 | 2,73 | 2,90 | ||
| 2,15 | 2,29 | 2,41 | 2,54 | 2,43 | 2,60 | 2,75 | 2,93 | ||
| 2,19 | 2,34 | 2,47 | 2,61 | 2,45 | 2,62 | 2,78 | 2,96 |
2.10. Екі орташа мәнді салыстыру
Аналитикалық практикада екі немесе одан да көп мәндерді салыстыру қажеттігі туындайды. Мысалы, бұл бір сынаманы екі түрлі әдіспен анықтағанда қажет. Бұндай жағдайда алдымен осы екі мәннің айырымы статистикалық маңызды ма жоқпа соны анықтап алған дұрыс. Оны F -критерийінің көмегімен жүзеге асырады:
 (2.23)
(2.23)
Бұндағы  - дисперсия мәнінен үлкен мән;
- дисперсия мәнінен үлкен мән;  – дисперсия мәнінен кіші мән, сондықтан F -критерийі қашанда бірден үлкен болады.
– дисперсия мәнінен кіші мән, сондықтан F -критерийі қашанда бірден үлкен болады.
2.7-кестеде әртүрлі ықтималдық пен бос дәрежедегі F -критерийінің сандық мәндері берілген. Егер (2.23) теңдеуі бойынша есептелген F -критерийінің мәні берілген ықтималдық пен бос дәрежедегі кестелік (Fкесте) мәндерден үлкен болса, онда дисперсиялар арасында белгілі айырым пайда болады. Егер, мысалы, қоланың құрамындағы қалайы анализінің бір сериясында алынған төрт анықтаудың ішінде дисперсияның мәні – 0,0132, ал басқа сериясында алты параллельді анықтаулардың дисперсиясы – 0,0262 болса, онда 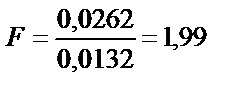 .
.
2.7-кесте
Р- ықтимиалдығына сәйкес F -критерийінің мәндері
| f1 | ||||||||||
| f2 | ||||||||||
| P=0,95 | ||||||||||
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,39 | 19,41 | 19,44 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,78 | 8,74 | 8,66 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,96 | 5,91 | 5,80 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,74 | 4,68 | 4,56 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,06 | 4,00 | 3,87 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,63 | 3,57 | 3,44 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,34 | 3,28 | 3,15 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,13 | 3,07 | 2,93 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,97 | 2,91 | 2,77 |
| P=0,99 | ||||||||||
| 98,49 | 99,00 | 99,17 | 99,25 | 99,30 | 99,33 | 99,36 | 99,40 | 99,42 | 99,45 | |
| 34,12 | 30,81 | 29,46 | 28,71 | 28,24 | 27,91 | 27,49 | 27,23 | 27,05 | 26,65 | |
| 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,80 | 14,54 | 14,37 | 14,02 | |
| 16,26 | 13,27 | 12,06 | 11,39 | 10,97 | 10,67 | 10,27 | 10,05 | 9,89 | 9,55 | |
| 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,10 | 7,87 | 7,72 | 7,39 | |
| 12,25 | 9,55 | 8,45 | 7,85 | 7,46 | 7,19 | 6,84 | 6,62 | 6,47 | 6,15 | |
| 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,03 | 5,82 | 5,67 | 5,36 | |
| 10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,80 | 5,47 | 5,26 | 5,11 | 4,89 | |
| 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,06 | 4,85 | 4,71 | 4,41 |
| P=0,999 | ||||||||||
| от 40000 до 600000 | ||||||||||
| 74,1 | 61,3 | 56,2 | 53,4 | 51,7 | 50,5 | 49,0 | 47,9 | 47,4 | 45,4 | |
| 47,0 | 36,6 | 33,2 | 31,1 | 29,8 | 28,8 | 27,6 | 26,9 | 26,4 | 24,8 | |
| 35,5 | 27,0 | 23,7 | 21,9 | 20,8 | 20,0 | 19,0 | 18,3 | 18,0 | 16,6 | |
| 29,2 | 21,7 | 18,8 | 17,2 | 16,2 | 15,5 | 14,6 | 13,9 | 13,7 | 12,4 | |
| 25,4 | 18,5 | 15,8 | 14,4 | 13,5 | 12,9 | 12,0 | 11,5 | 11,2 | 10,0 | |
| 22,9 | 16,4 | 13,9 | 12,6 | 11,7 | 11,1 | 10,4 | 9,8 | 9,6 | 8,5 | |
| 21,0 | 14,9 | 12,6 | 11,3 | 10,5 | 9,9 | 9,2 | 8,7 | 8,5 | 7,2 |
2.7- кестесі бойынша f1 =5, f2= 3және P=0,99 мәніндегі F -критерийі: F0,99; 5; 3 = 28,24, ал P=0,95 болғанда F0,99; 5; 3 = 9,01. Демек 5% – дық мәнділік деңгейінде ауытқулардың айырымы оншалықты үлкен емес, сондықтан осы екі мәнді бірдей іріктеуге жатқызса болады.
Егер F -критерийі бойынша дисперсиялар айырымы үлкен болса,онда 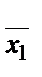 және
және  орташа мәндерін өзара салыстыру мүмкін болмас еді. Дисперсиялар айырымы оншалықты үлкен болмаған жағдайда орташа іріктелген дисперсияны табуға болады:
орташа мәндерін өзара салыстыру мүмкін болмас еді. Дисперсиялар айырымы оншалықты үлкен болмаған жағдайда орташа іріктелген дисперсияны табуға болады:
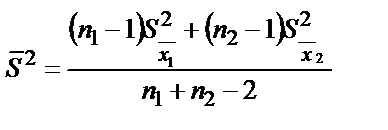 (2.24)
(2.24)
және t -критерийі есептеледі:
 (2.25)
(2.25)
Егер нәтижелердің бірі теориялық есептеу жолымен алынған болса, онда t -критерийін есепетеу оңайырақ болады. Бұл кезде мына теңдеу қолданылады:
 (2.26)
(2.26)
Егер (2.25) теңдеуі бойынша есептелген t -критерийінің мәні берілген мәнділік деңгейінде және бос дәреже санында f = n1 + n2 – 2, t -критерийінің кестелік мәнінен жоғары болса, онда  және
және  мәндерінің айырымы айтарлықтай болады.
мәндерінің айырымы айтарлықтай болады.
Енді, қоланың құрамындағы қалайыны екі әдістеме бойынша анализдеу кезінде алынған нәтижелердегі айырмашылық айтарлықтай ма жоқпа соны анықтайтын болсақ. Бір әдістемемен жүргізілген төрт параллельді сынаманың анализі бойынша қоладағы қалайының массалық үлесі 4,72 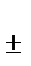 0,18, ал алты параллельді сынаманың басқа әдіспен алынған нәтижелері 4,92
0,18, ал алты параллельді сынаманың басқа әдіспен алынған нәтижелері 4,92  0,16 болған. (2.23) теңдеуі бойынша есептеулер екі дисперсияның арасында айтарлықтай айырмашылық болмайтынын көрсетті, сондықтан (2.24) теңдеуі бойынша орташа дисперсияны табамыз:
0,16 болған. (2.23) теңдеуі бойынша есептеулер екі дисперсияның арасында айтарлықтай айырмашылық болмайтынын көрсетті, сондықтан (2.24) теңдеуі бойынша орташа дисперсияны табамыз:
Одан әрі (2.25) теңдеуі бойынша t -коэффициентін есептейтін болсақ:
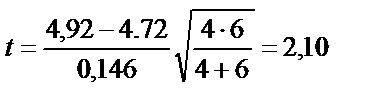
2.4-кестесіндегі 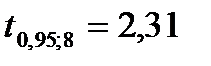 , яғни
, яғни 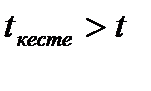 , демек, екі нәтиженің арасында айтарлықтай айырмашылық жоқ.
, демек, екі нәтиженің арасында айтарлықтай айырмашылық жоқ.
2.11. Анықтау шегі. Анықталатын мөлшерлердің диапазоны
Кездейсоқ шамалардың таралу параметрлері арқылы анықтауға болатын кейбір түсініктерді қарастырсақ. Бұл алдымен әдістің немесе әдістеменің сезімталдық сипаттамасы. Сезімталдық сипаттамасы дегеніміз – анықтау шегі және анықталатын мөлшерлердің ең төменгі мәні.
Анықтау шегі cmin,P – компоненттің мөлшерін берілген әдістеме бойынша, берлгілі бір сенімді ықтималдықпен анықтауға болатын ең аз мөлшер. Сонымен, анықтау шегі түсінігі сандық анализдің ұғымдарына жатады және компоненттің мейлінше жоғары ықтималдықпен (Р = 0,95 немесе Р = 0,99) анықталуы мүмкін минимальды мөлшерін mmin (немесе минимальды концентрациясын cmin) анықтайды. Анықтау шегі, бақылау тәжірибесінің сигналынан уфон өзгеше болатын, минимальды аналитикалық сигналмен де ymin берілуі мүмкін. Минимальды аналитикалық сигнал компонентті анықтауда қателерді болдырмайтындай етіп таңдалуы керек. Анықтау шегінің сандық мөлшерін төмендегідей теңдеумен анықтауға болатыны статистикалық әдістермен дәлелденген:
 (2.27)
(2.27)
бұндағы sфон – фонның аналитикалық сигналының стандартты ауытқуы; S – сезімталдық коэффициенті.
Анықтау шегін есептеудің басқа да әдістері бар, бірақ (2.27) теңдеуін жиі қолданады.
Анықталатын минималды аналитикалық сигнал, сонымен бірге анықтау шегі фондық сигналдың орташа деңгейімен емес, осы сигналдың орташа мәнімен (sфон) салыстырғандағы ауытқу аумағымен анықталатынын атап көрсетеміз. Бұл шаманы параллельді анықтаулардың жеткілікті санынан (п≥ 20) анықтаған жөн.
Әдетте сандық химиялық анализде анықталатын мөлшерлердің диапазоны келтіріледі. Анықталатын мөлшерлердің диапазоны дегеніміз – берілген әдістеме бойынша анықталатын мөлшерлердің төменгі және жоғарғы мәндерімен шектелген анықталатын мөлшерлер шамасының аумағы. Жоғарғы шекара (mж, сж) – компоненттің берілген методика бойынша анықтауға болатын ең үлкен сандық мөлшері немесе концентрациясы. Бұл шама зерттелген интервалмен немесе аналитикалық сигналды жеткілікті дәлдікпен өлшеу мүмкіндігімен шектелген. Мысалы, фотопластинканың қараю интенсивтігі немесе үдеріс жылдамдығы өте үлкен болуы мүмкін, сондықтан оларды қажетті дәлдікпен өлшеу қиын болады. Әдетте аналитик үшін анықталатын мөлшердің төменгі шекарасын ( mт, ст ), яғникомпоненттің берілген әдістеме арқылы
2.6-сурет. Анализ нәтижелерінің салыстырмалы стандартты ауытқуының анықталатын компоненттің концентрациясына тәуелділігі. | анықтауға болатын ең аз мөлшерін білу маңызды. Төменгі мөлшер аумағында sr шамасы мөлшер төмендеген сайын өседі (2.6-сурет), ал анализ нәтижесінің дәлдігі, сәйкесінше, нашарлайды. Әдетте, анықталатын мөлшерлердің төменгі шекарасы ретінде sr ≤ 0,33 |
болғаннан бастап анықтауға болатын минимальды санды немесе концентрацияны алады.
Нақты мақсаттарға байланысты sr мәнінің басқа да шекті мүмкін мәні көрсетілуі мүмкін. Сонымен бірге, кейде анықталатын концентрацияның төменгі шекарасы ретінде kcmin,P -ге тең шаманы алады, мұндағы коэффициент k әдетте 2-ден 10-ға дейінгі мәндерге тең деп алынады.
Бақылау сұрақтары мен жаттығулар
1. Химиялық анализ әдістері мен әдістемелерінің метрологиялық сипаттамаларын атаңыз.
2. Келесі реакциялардағы эквивалентті, эквиваленттік факторды және эквиваленттің молярлы массасын көрсетіңіз:
H2PO3+KOH KH2PO4+H2O
H2PO3+2KOH K2HPO4+2H2O
H2PO3+3KOH K3PO4+3H2O
H2C2O4+2KOH K2C2O4+2H2O
2HCl+Ba(OH)2 BaCl2+2H2O
2RCOOH+ Ba(OH)2 Ba(RCOO)2+2H2O
2KCN+AgNO3 KAg(CN)2+KNO3
CuSO4+2KI CuI+1/2I2+K2SO4
2KMnO4+5H2C2O4+3H2SO4 K2SO4+2MnSO4+10CO2+8H2O
4KMnO4+5As2O3+12HCl 4KCl+4MnCl2+As2O5+6H2O
FeCl3+TiCl3 FeCl2+TiCl4
SnCl2+Fe2(SO4)3+2HCl SnCl4+2FeSO4+H2SO4
3. Бақылау тәжірибесін жүргізген кезде аналитикалық сигналдың шамасына әсер ететін қандай факторларды ескеру қажет?
4. Егер а) аналитикалық сигнал-құрам функциясы түзу емес; б) үлгінің матрицасы аналитикалық сигналға айтарлықтай әсер ететін болса компоненттің құрамына қандай есептеу әдісін қолдану қажет?
5. Анализдің дұрыстығын қандай әдістермен тексеруге болады?
6. Гравиметриялық және титриметриялық әдістердегі жүйелі қателіктердің белгілі көздерін атаңыз.
7. Жүйелі қателердің кездейсоқ қателерден айырмашылықтары қандай?
8. Химиялық анализ мәліметтерінің таңдамалы бірлігінің өнімділігін қандай шамалар сипаттайды?
9. Компонентті анықтаудың сезімталдығын арттыру үшін қандай әдістерді қолдануға болады?
10. Жүйелі және кездейсоқ қателер мен өрескел қатенің себептері қандай?
11. Анализдің кездейсоқ қатесі қалай сипатталады?
12. Анализ нәтижесінің дәлдігін бағалау үшін қандай мәнді қолданады?
13. Сенімді аралық неге тең және ол немен сипатталады?
14. Әдістің жүйелі қатесін табу үшін сенімді аралықты қалай қолданады?
15. Орташа мәннің стандартты ауытқуын қалай есептейді?
16. Q -критерийі деген не және ол қандай факторларға байланысты болады?
17. Әдістің жүйелі қатесін анықтау үшін ықтималдық интервалын қалай қолданады?
18. Анықтаудың дәлдігі деген не?
1. Сұрыптаудың стандартты ауытқуын (Sx) қайсы формула бойынша есептеу қажет?
1)  ; 2)
; 2)  ; 3)
; 3) 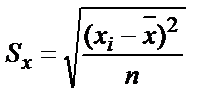 ;
;
4) 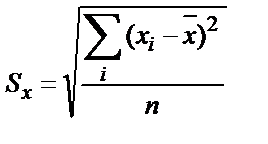 ; 5)
; 5)  .
.
2. Салыстырмалы стандартты ауытқу шамасы қайсы формула бойынша есептелінеді?
1)  ; 2)
; 2) 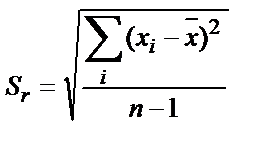 ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 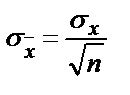 .
.
3. Қандай шамалар анализ нәтижелерінің қайталанымдылығын сипаттайды?
1) сенімді аралық;
2) бас жиынтықтың стандартты ауытқуы (?х) және сұрыптаудың стандартты ауытқуы (Sx);
3) анализ топтамасы (сериясы) нәтижелерінің орта мәні;
4) анализ нәтижелерінің жүйелі айырмашылығы;
5) барлық келтірілген шамалар.
4. Аз өлшеулер үшін өрескел қатені қалай бағалауға болады?
1) Sr шамасы бойынша;
2)  қатынасы бойынша есептелген Q мәнін таблицалық
қатынасы бойынша есептелген Q мәнін таблицалық  мәнімен салыстыру: егер
мәнімен салыстыру: егер  болса, онда өрескел қате бар екені дәлелденеді;
болса, онда өрескел қате бар екені дәлелденеді;
3) нәтижелерді мөлшерлеу (нормалау) және шеткі мәндерді алып тастау;
4) F-критерийді таблицалық мәнмен F(f1,f2,p) салыстыра отырып пайдалану: егер F > F(f1,f2,p) болса, онда өрескел қатенің бар екені дәлелденеді;
5) дұрыс жауабы келтірілмеген.
5. Көрсетілген факторлардың қайсысы ерітінді көлемін өлшем колбасымен өлшеуде жіберілетін жүйелі қателіктің себебі бола алады?
1) колбаның ішкі бетінің лас болуы;
2) зерттелетін сұйықтықтардың әртүрлі құрамы;
3) колба белгісінің дұрыс салынбауы;
4) көлемнің колба белгісі бойынша дәл өлшенбеуі;
5) колба ішіндегі заттың араластырылмауы.
6. Жүйелі қателіктерді қалай жоюға болады?
1) жүйелі қателіктерді тәжрибені көп қайталап жүргізу арқылы жоюға болады;
2) жүйелі қателіктерді жоюға болмайды;
3) жүйелі қателіктерді өлшем ыдыстарын, аспаптарды калибрлеу арқылы және нәтижелерді стандарттармен салыстыру арқылы жоюға болады;
4) жүйелі қателіктер екі аналитиктің алған нәтижелерін салыстыру арқылы жойылады;
5) дұрыс жауабы келтірілмеген.
7. Q-критерий не үшін пайдаланылады?
1) әр түрлі топтамалар (серия) тәжрибелерінің салыстырмалылығын анықтау үшін;
2) орта мәннің қателігін анықтау үшін;
3) жеке өлшеудің қателігін анықтау үшін;
4) өрескел қателіктерді анықтау үшін;
5) тура өлшеудің дәлдігін анықтау үшін.
8. "Бос бақылау тәжірибесі" қандай мақсатта жүргізіледі?
1) өлшем ыдыстарының қателіктерін жою үшін;
2) өлшеу аспаптарының қателіктерін жою үшін;
3) өлшеу қателіктерін жою үшін;
4) реактивті жүйелі қатені жою үшін және градуирлеу графигінің дәлдігін (барабарлығын) дәлелдеу үшін;
5) дұрыс жауабы келтірілмеген.
9. “Анықталатын мөлшердің төменгі шекарасы” деп нені түсіну керек?
1) компонентті анықтау дәлдігі;
2) берілген қателіктен (Sr =0,33 немесе 0,5%) аспай аныталуы м‰мкін минимальды мөлшер не концентрация;
3) p=0,99 болғандағы сенімді аралық шамасы;
4) анықтау шегі;
5) нәтижелер айырмашылығының мүмкіндігінше минимальды аз болуы.
10. Жүйелі қателіктерді қандай тәсілдермен анықтап табуға болады?
1) сынама мөлшерін өзгерту арқылы;
2) "енгізілген – табылған" тәсілі бойынша жұмыс істеу арқылы;
3) берілген нәтижені тәуелсіз әдіспен алынған нәтижемен салыстыру арқылы;
4) стандартты затты анализдеу арқылы;
5) барлық көрсетілген тәсілдер жарайды.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1647; Нарушение авторских прав?; Мы поможем в написании вашей работы!