T- таралу

.

Есептеулер нәтижесі (2.14) теңдеуі бойынша μ – σ – дан μ + σ – ға дейінгі интегралы 68,3% – ауданын құрайды, μ 2 σ аралығында ол 95%, ал μ 3 σ аралығында интеграл таралу қисығы және абсцисса өсімен шектелетін ауданды түгел алады (99,7%). (2.14) теңдеуі бойынша интеграл х_{і –} нәтижесінің пайда болу ықтималдығы Р-ның x kσ (x – kσ – дан x + kσ – ға дейінгі) ауданда болатынын көрсетеді. Ықтималдылықтың бұл аралы­ғын сенімді ықтималдылық немесе статистикалық сенімділік деп атайды, μ – kσ- дан μ + kσ- ға дейінгі интервалды сенімді интервал, ал интервал шекарасын – сенімді шекара дейді. Осылайша, μ – σ – дан μ + σ – ға дейінгі аралықтағы нәтижені алудың сенімді ықтималдығы 68,3% болады, яғни бұл аралықта барлық нәтижелердің 2/3 орналасады. 2 σ аралығында мәндердің 95% орналасады, ал 3 σ ауданында 99,7%, яғни нәтижелердің барлығы дерлік осы аралықта болады. Интегралдау аралығынан тыс болатын нәтиже алу ықтималдығы 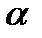-мен анықталады:

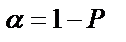
Бұл шаманы мәндер ықтималдығының деңгейі деп атайды. Қалыпты таралуға негізделген қателердің классикалық теориясы астрономияда, геодезияда және т.б. бір мәннің көп нәтижесі алынатын есептеулерде кең түрде қолданылады. Алайда бұл тәсіл заттар анализінің нәтижесін өңдеуде тиімді болмай шықты, өйткені ол нәтиженің төмендеуіне әкеліп соқты. Сондықтан қатені анықтаудың ең тиімді және дұрыс тәсілі ретінде t- таралу, яғни Стьюдент таралу тәсілін айтуға болады. Бұл аз шамаларды статистикалық өңдеу болып табылады.

Таңдалған дисперсияның басты дисперсияға жақындатылу дәрежесі бос дәреже санына f байланысты болады, оны мына теңдікпен анықтайды:

f=n-1

бұндағы n – өлшеулер саны, ол параллельді сынамаларға тең болады.

Бос дәрежелер саны неғұрлым кіші болған сайын, соғұрлым таңдамалы дисперсияның S² басты дисперсияның σ² сенімді сипаттамасы болу мүмкіндігі төмен. Қалыпты таралу кезінде кіші қателерге қарағанда үлкен қателердің пайда болу ықтималдығы төмен. Сондықтан параллельді сынамалар санын азайтқанда үлкен қателердің пайда болу ықтималдығы да төмендейді. Бұны ескермеген жағдайда қатенің мәні төмендеп, нақты дұрыс мән алу мүмкін болмайды. Анықтаулар (параллельді сынамалар) санымен байланысты сенімсіздік Стьюденттің t- таралуы арқылы ескеріледі. Қалыпты таралуға қарағанда Стьюденттің t- таралуында кіші қателерден гөрі үлкен қателердің пайда болу мүмкіндігі көбірек деп қарастырылады.

Қалыпты таралу сияқты t- таралуда симметриялы және оның да максимумы абсциссаның қалыпты таралудағыдай мәнінде болады. Алайда t- таралудағы биіктігі мен ені сияқты сипаттамалары бос дәреже санына, яғни өлшемдер санына байланысты болады (2.5-сурет).

Y(х)

x  

2.5-сурет. Таралу қисығы.

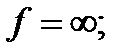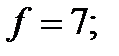1- ; 2- 3-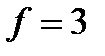

2.5- суреттен бос дәреже саны азайған сайын қисықтың аласарып, абсцисса осіне жақындай түсетінін көруге болады. 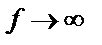t- таралу қалыпты таралуға ауысады. Бұл айырмашылық 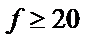болғанда азайып, білінбей кетеді.

Егер қалыпты таралу жағдайында өлшемдер саны көп болғанда μ 2 σ сенімді аралығында сенімді ықтималдық 95% болса, онда өлшемдер саны аз болғанда сенімді ықтималдықтың берілген мәні мынадай сенімді аралықта іске асады: 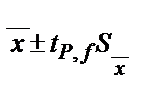. Бұндағы 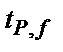-Стьюдент коэффициенті, ол қалыпты таралудағы, t- таралудағы және берілген Р-дағы айырмашылықты ескереді.

t - ның индексі Р бос дәреженің белгілі f мәніндегі ықтималдықты көрсетеді. 2.4- кестеде Р мен f -тің әртүрлі мәндеріндегі Стьюдент коэффициенттері берілген.

2.4- кесте

Стьюдент коэффициенттері (t _{p, f})

f	P
0,75	0,90	0,95	0,98	0,99
	2,41	6,31	12,71	31,82	63,66
	1,60	2,92	4,30	6,97	9,92
	1,42	2,35	3,18	4,54	5,84
	1,34	2,13	2,78	3,75	4,60
	1,30	2,01	2,57	3,37	4,03
	1,27	1,94	2,45	3,14	3,71
	1,25	1,89	2,36	3,00	3,50
	1,24	1,86	2,31	2,90	3,36
	1,23	1,83	2,26	2,82	3,25
	1,22	1,81	2,23	2,76	3,17
	1,21	1,80	2,20	2,72	3,11
	1,21	1,78	2,18	2,68	3,05
	1,20	1,77	2,16	2,65	3,01
	1,20	1,76	2,14	2,62	2,98
	1,20	1,75	2,13	2,60	2,95
	1,19	1,75	2,12	2,58	2,92
	1,19	1,74	2,11	2,57	2,90
	1,19	1,73	2,10	2,55	2,88
	1,19	1,73	2,09	2,54	2,86
	1,18	1,73	2,09	2,53	2,85
	1,17	1,70	2,04	2,46	2,75
	1,17	1,68	2,02	2,42	2,70
	1,16	1,67	2,00	2,39	2,66
	1,16	1,66	1,98	2,36	2,62
¥	1,15	1,64	1,96	2,33	2,58

f – тіңаз мәнінде қалыпты таралу мен t-таралудың арасындағы айырмашылық айтарлықтай болады, мысалы, f=3 және Р= 95% t_{p, f} =3,18, ал оның қалыпты таралудағы мәні 2 болады. Орташа арифметикалық шаманың мүмкін болатын салыстырмалы қатесін (салыстырмалы ауытқуды) мына теңдеумен анықтайды:

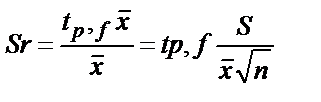
Берілген сенімді Р ықтималдықтағы сенімді аралық мынаған тең:

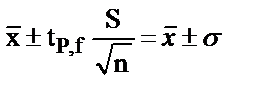( 2.15)

егер

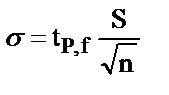(2.16)

бұндағы берілген сенімді Р ықтималдықтағы және бос дәреженің f санындағы анализдің мейлінше ықтимал қатесі.

Нақты мән, немесе басты орташа, 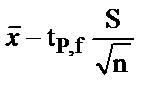пен 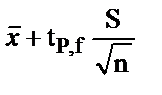арасында орналасады, бұл аралық сенімді шекара деп аталады. Бұл аралықтан тыс нәтиже алу ықтималдығының қаупі бірден өзгеше (1-Р), сенімді аралықты сенімді ықтималдықпен сипаттайды және оны да бос дәреже саны сияқты көрсету міндетті. Анализ нәтижесінің сенімді интервалын әдетте 95% – дық сенімді ықтималдықпен есептейді.

( 2.15) теңдеуінен анықтаулар саны n неғұрлым көп болған сайын, соғұрлым берілген сенімді ықтималдықтағы сенімді аралық кішкентай болады, яғни анализдің дәлдігі де соғұрлым жоғары болады. Мысалы, 95% – дық сенімді ықтималдықта екі параллельді анықтаулар үшін сенімді арлық (2.16) теңдеуіне сәйкес 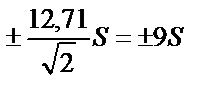, үш анықтау үшін 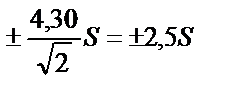, төрт анықтау үшін және бес анықтау үшін

Осыдан, сенімді аралыққа және қатені азайтуға мейлінше тиімді әсер ететін параллельді анықтаулар саны 4-5 –ке дейін ғана, параллельді анықтаулар санын одан әрі өсірудің оншалықты әсері байқалмайды. Сондықтан төрттен көп параллельді анықтауларды тек арнайы жағдайларда ғана, мысалы, кейбір арбитражды анализдерде ғана жүзеге асырады.

2.8. Қосынды мен көбейтіндінің қатесі

Химиялық және аналитикалық есептеулерде көбінесе өлшенген мәндердің айырымын, олардың қосындысын, көбейтіндісін және т.б. қолданады. Мысалы, гравиметриялық анализдегі тұнбаның массасын, анықталатын компоненттің жарық жұтуын және т.б. осы жолмен анықтайды. Сондықтан айырымдағы немесе көбейтіндідегі қатені есептеудің тікелей практикалық мәні зор.

Ықтималдық теориясы бойынша кездейсоқ мәндердің дисперсиясына аддитивтілік қасиеті тән, стандартты ауытқуда бұндай қасиет жоқ. Сондықтан бірнеше мәндердің x₁, x₂, … қосындысы немесе айырымы мынаған тең болады:

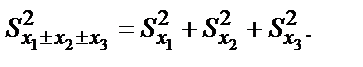
Көбейтінді немесе бөлшек болған кезде салыстырмалы қателердің дисперсиясының қосындысы алынады:

Дата добавления: 2014-11-25