Алыпты таралу 4 страница

және 2.8 – теңдігі бойынша орташа нәтиженің стандартты ауытқуын анықталады:

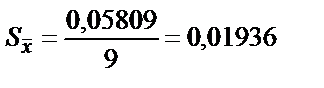
Микрокалькуляторлардың қайсыбірінде, мысалы «Электроника МК-51» статистикалық есептеу режимі қарастырылған. Олар ∑x_i², 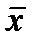, S және x_i шамасын енгізу арқылы алынатын басқа да мәндерді алуға болады.

Экспериментальдық нәтижелерді талдай отырып, кіші қателермен салыстырғанда мәні үлкен болатын қателердің аз болатындығын байқауға болады. Сонымен қатар, байқаулар санын арттырған сайын таңбалары әртүрлі және мәндері бірдей қателер жиі кездеседі. Осы және бұдан да басқа кездейсоқ қателердің қасиеттері қалыпты таралумен немесе Гаусс теңдігімен өрнектеледі:

(2.13)

бұндағы – ықтималдылық жиілігі;

x – кездейсоқ шаманың мәні;

μ – басты орташа (математикалық күтім);

σ – дисперсия.

2.4 – суретте аудандары бірдей болатын қалыпты таралу қисығы берілген. Суреттен стандартты ауытқу (дисперсия) үлкен болған сайын, қисықтың жалпақ дөңесті болатынын көруге болады. μ және σ шамалары таралу параметрлері деп аталады. Ықтималдылық жиілігі (2.13) теңдеуімен өрнектеледі.

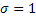
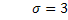Y(x)           x

2.4-сурет. Әртүрлі орташа

квадратты қателіктер

кезіндегі қалыпты таралу

қисықтары

коэффициентін таңдағанда кездейсоқ x мәнінің 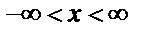интервалына түсу ықтималдығы бірге тең болатындай мәнін алады.

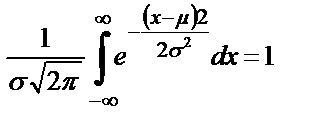(2.14)

μ мен σ – ның кез-келген мәнінде 2.13 теңдеуі қисығымен және абсцисса өсімен шектелетін аудан бірге тең болады. Егер x₁ және x₂ мәндерін ордината өсіне салсақ, онда кездейсоқ x шамасының x₁<x<x₂ интервалына түсу ықтималдығы төмендегідей

Дата добавления: 2014-11-25