Решение

h=50 м

H=150 м

а=500

a+b=800

g=10 м

u_{o min} -?

a_m -?

Исследуем уравнение траектории мины (см. задачу 6):

.

Выделим траектории, которые проходят через цель с координатами x=(a + b), y=h:

.

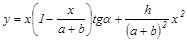При этом начальная скорость мины должна удовлетворять условию

.

Среди этих траекторий для нас интерес представляют те, которые огибают гору. Допустим, что условие у(а)>Н выполнено. Исследуем зависимость u₀²(tga). Эта функция имеет минимум при

.

Решение со знаком “-” не удовлетворяет условию .

Минимальная начальная скорость при этом равна

.

В частном случае (h = 0) (цель находится у подножья горы)

.

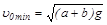Если у(а)<H при угле a_m, тонеобходимо выбрать траекторию, которая касается вершины горы. Из условия y(a)=H находим для угла a соотношение

.

Соответствующая этому углу a начальная скорость мины равна

.

В частном случае (h=0)

.

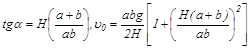Рассмотрим, к какому случаю относятся наши данные. Вычислим tga_m = 1, 064, a_m = 46, 8⁰. Тогда у(а)= 180 м. Таким образом, так как у(а)>H = 150 м, стрельба должна вестись под углом a_m» 47⁰ при минимальной скорости мины u_{0 min} = 92 м/с.

Задача 9. Точка движется с постоянной по величине скоростью (u =const) по плоской криволинейной траектории (см. рисунок). Сравните ускорение точки в положениях А и В.

Решение. Правильный ответ: а _А> а _В.

Эта качественная задача связана с выяснением знания определений таких кинематических величин, как касательное, нормальное и полное ускорения. По определению касательное ускорение характеризует изменение величины скорости

.

В нашем случае величина скорости не изменяется, поэтому а_t = 0.

Величина нормального ускорения в каждой точке траектории связана с радиусом кривизны соотношением:

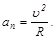
Модуль полного ускорения равен

Таким образом, а _А > a _B , так как u=const, R _A < R _B.

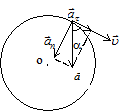Задача 10. При движении точки по окружности угловая скорость изменяется с течением времени согласно соотношению w~tⁿ >, где n > 0. При этом тангенс угла между вектором ускорения и вектором скорости изменяется с течением времени как t^m. Определите значение m.

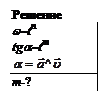
Для плоского движения ускорение можно представить как сумму касательного и нормального ускорений:

.

Откуда 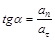(см. рисунок).

Учитывая, что

,

,

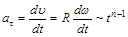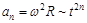так как R=const, находим

Таким образом, m = n + 1.

Задача 11. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворот j согласно уравнению w=w₀-aj, где w₀ = 12 рад/с, a = 0, 15 1/с. Определите предельные значения угла поворота и угловой скорости, если в начальный момент времени j (0)= 0.

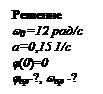
Найдем уравнение вращательного движения твердого тела j(t). Угловая скорость по определению равна:

.

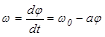Интегрируя последнее уравнение с учетом j (0)= 0, получаем

.

Подставив j(t) в выражение для угловой скорости, находим

.

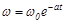В пределе при t ®¥

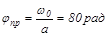, w_пр=0.

Задача 12. Самолет, летящий горизонтально со скоростью u₀, начинает подниматься вверх, описывая окружность, лежащую в вертикальной плоскости. Скорость самолета при этом меняется с высотой h над первоначальным уровнем движения согласно соотношению u² = u₀² - na₀h, где а₀=10 м/с², n=3. В верхней точке траектории его скорость оказывается равной . Определите ускорение а самолета в тот момент, когда его скорость составляет угол j=90⁰ с горизонтом.

Решение. Величина полного ускорения самолета равна

,

где .

Выразим высоту самолета через угол j и радиус окружности R (см. рисунок):

.

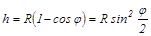Закон изменения скорости будет иметь вид

.

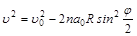По условию 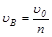при j = p. Тогда квадрат начальной скорости равен

.

Для нормального и касательного ускорений в произвольной точке окружности получаем

,

.

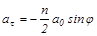Полное ускорение равно

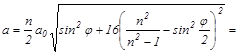40 м/с².

Дата добавления: 2014-11-25