
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач 1 страница
|
|
|
|
Законы сохранения
Законы сохранения энергии, импульса и момента импульса являются наиболее общими (фундаментальными) законами физики, которым подчиняются все известные современной физике явления природы.
Решение динамических задач часто облегчается использованием законов сохранения, например в задачах о движении космических аппаратов.
Законы сохранения энергии и импульса являются единственным средством теоретического анализа процессов столкновения и распада тел (частиц), когда характер действующих сил неизвестен.
Результаты столкновения могут быть самыми разнообразными: тела могут соединяться в одно тело (абсолютно неупругий удар), тела могут расходиться без изменения своего внутреннего состояния (абсолютно упругий удар), могут возникнуть новые тела. Столкновение макротел всегда является в той или иной степени неупругим, однако в области атомной, ядерной физики и процессов с элементарными частицами понятие об упругом ударе играет важную роль, так как благодаря дискретному характеру энергетического спектра сталкивающихся частиц их внутреннее состояние либо не меняется вообще (упругий удар), либо скачком изменяется на конечную величину.
При распаде тел (частиц) наблюдается частичное превращение внутренней энергии в кинетическую энергию продуктов распада.
Задача 19. На неподвижный бильярдный шар налетает другой. Найдите угол разлета шаров после нецентрального столкновения. От чего зависит направление движения каждого шара после столкновения?
Решение. Столкновение называется нецентральным, если направление движения центра налетающего шара не совпадает с прямой, соединяющей центры шаров. Расстояние между указанными прямыми называется прицельным.
Примем столкновение между шарами абсолютно упругим. Тогда для сталкивающихся шаров можно записать закон сохранения импульса и энергии в следующем виде:
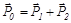 ,
,
 ,
,
где  – импульс и кинетическая энергия налетающего шара до столкновения,
– импульс и кинетическая энергия налетающего шара до столкновения,  – импульс и кинетическая энергия налетающего шара после столкновения,
– импульс и кинетическая энергия налетающего шара после столкновения, 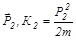 – импульс и кинетическая энергия неподвижного шара после столкновения.
– импульс и кинетическая энергия неподвижного шара после столкновения.
Как следствие из закона сохранения механической энергии, получается следующее соотношение для импульсов шаров:
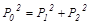 .
.
Возведем в квадрат уравнение для импульсов:
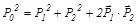 .
.
Законы сохранения импульса и энергии совместимы, если скалярное произведение импульсов шаров после столкновения равно нулю:
 .
.
Так как Р1 ≠ 0, Р2 ≠ 0, то cosα=0. Откуда следует, что 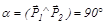 .
.
 После нецентрального упругого столкновения бильярдные шары разлетаются под прямым углом.
После нецентрального упругого столкновения бильярдные шары разлетаются под прямым углом.
Направление движения каждого шара после столкновения определяется прицельным растоянием а (см. рисунок).
Из рисунка видно, что направление движения первоначально неподвижного шара после столкновения составляет угол
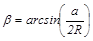
с направлением движения налетающего шара (R – радиус шара).
Задача 20. Два шара c массами m1=1,2кг и m2=2,1кг движется со скоростями u1=5,6м/с и u2=2,7м/с соответственно по прямой, соединяющей их центры. С первым шаром связана легкая пружина жесткостью k=12кН/м. Определите максимальное сжатие пружины при столкновении шаров.
Решение. Воспользуемся ИСО, связанной с центром масс шаров.
Скорость центра масс равна
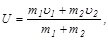
а импульсы шаров в ИСО центра масс равны
p1=m1(u1-U)=m(u1-u2),
p2=m2(u2-U)=-m(u1-u2),
где 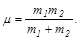
Кинетическая энергия шаров до столкновения равна
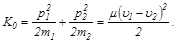
Так как в процессе столкновения механическая энергия системы сохраняется,
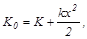
то, очевидно, максимальная потенциальная энергия деформации пружины равна начальной кинетической энергии шаров (К=0):
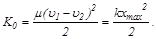
Откуда получаем
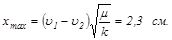
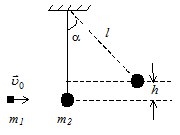 Задача 21. В тело массой m2 = 2, 5кг, подвешенное на нерастяжимой нити длиной l = 1, 1м, попадает горизонтально летящее тело массой m1 = 1, 5кг и слипается с ним. Определите начальную скорость налетающего тела u0 (м/с), если нить отклонилась на угол α = 40 ˚ от положения равновесия.
Задача 21. В тело массой m2 = 2, 5кг, подвешенное на нерастяжимой нити длиной l = 1, 1м, попадает горизонтально летящее тело массой m1 = 1, 5кг и слипается с ним. Определите начальную скорость налетающего тела u0 (м/с), если нить отклонилась на угол α = 40 ˚ от положения равновесия.
Решение. Столкновение является абсолютно неупругим. Пренебрегая временем столкновения, можно записать
Р0=Р,
где Р0=m1u0 , P=(m1+m2)u (u – скорость тел после столкновения).
Сохраняется ли механическая энергия системы при неупругом столкновении тел?
Найдем значение кинетической энергии системы после столкновения:
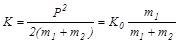 ,
,
где 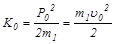 – кинетическая энергия налетающего тела.
– кинетическая энергия налетающего тела.
При неупругом столкновении часть или вся кинетическая энергия системы переходит во внутреннюю энергию сталкивающихся тел:
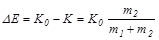 .
.
Как видно, относительная доля превращающейся энергии определяется отношением масс сталкивающихся тел:
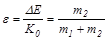 .
.
После столкновения система тел поднимается на высоту h (см. рисунок), которая связана с углом отклонения a следующим соотношением:
 . (1)
. (1)
Очевидно, высота h будет определяться величиной кинетической энергии системы после столкновения и сопротивлением воздуха.
Пренебрегая сопротивлением воздуха, для оценки высоты h проще воспользоваться законом сохранения механической энергии:
К1+П1=К2+П2.
Так как
К2=0, П2-П1=(m1+m2)gh,
 ,
,
для высоты h получаем:
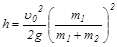 . (2)
. (2)
Приравняв выражения (1) и (2), находим
 =3,6м/с.
=3,6м/с.
Как следствие из последнего соотношения, получается расчетная формула для экспериментального определения скорости пули методом баллистического маятника:
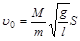 ,
,
где S – горизонтальное смещение маятника, M – масса маятника, m – масса пули.
Задача 22. По гладкой горизонтальной поверхности движется тело массой m1=1, 5кг со скоростью u1=12м/с и сталкивается с неподвижным телом массой m2=2, 5кг. При столкновении выделяется теплота Q = 34Дж. Определите скорость тел после столкновения.
Решение. Сначала выясним, не является ли столкновение абсолютно неупругим. Найдем количество теплоты, которое выделяется при абсолютно неупругом столкновении (см. задачу 21):
 =67,5Дж.
=67,5Дж.
Т.к. Q<Qн,то это означает, что при столкновении тела не слипаются.
Динамическое решение проблемы невозможно из-за отсутствия сведений о характере силового взаимодействия во время столкновения тел. В этих условиях продвинуться в разрешении проблемы помогают фундаментальные законы сохранения.
Запишем законы сохранения импульса и энергии для неупругого центрального столкновения тел:
 ,
,
 ,
,
где 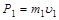 ,
, 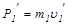 ,
,  ,
,  ,
,  ,
,  (
( и
и  – скорости тел после столкновения).
– скорости тел после столкновения).
Уравнения сохранения содержат неизвестные значения 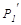 и
и 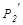 (импульсы тел после столкновения). Таким образом, проблема сводится к решению системы двух уравнений с двумя неизвестными величинами.
(импульсы тел после столкновения). Таким образом, проблема сводится к решению системы двух уравнений с двумя неизвестными величинами.
Представим систему уравнений в безразмерной форме:
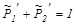 ,
,
 ,
,
где  ,
, 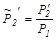 ,
,  ,
, 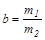 .
.
Решив систему уравнений, для неизвестных значений 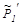 и
и  получим:
получим:
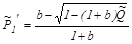 ,
,
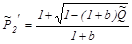 .
.
Для численных значений в условии задачи
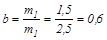 ;
;
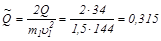 ;
;
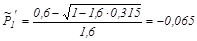 ;
;
 .
.
Скорости тел после столкновения равны
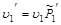 = 12 (- 0, 065)=- 0, 78м/с;
= 12 (- 0, 065)=- 0, 78м/с;
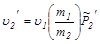 = 12 × 0, 6 × 1, 065 = 7, 7м/с.
= 12 × 0, 6 × 1, 065 = 7, 7м/с.
Полученное решение содержит предельные случаи абсолютно упругого столкновения (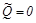 ) и абсолютно неупругого столкновения (
) и абсолютно неупругого столкновения (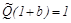 ). Убедитесь в этом самостоятельно.
). Убедитесь в этом самостоятельно.
Задача 23. На гладкой горизонтальной поверхности находятся два тела массами m1 и m2 (m1=km2), между которыми зажата легкая пружина. Горизонтальная поверхность плавно переходит в гладкие горки (см. рисунок). Определите отношение высот подъёма тел h2/h1 после распрямления пружины, если k=2.
Решение. Высота, на которую поднимается тело в отсутствие трения и сопротивления воздуха, однозначно определяется начальной 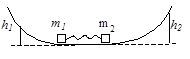 кинетической энергией, которую оно приобретает при распрямлении пружины, как следствие закона сохранения механической энергии:
кинетической энергией, которую оно приобретает при распрямлении пружины, как следствие закона сохранения механической энергии:
К0+П0=К+П.
В максимальной точке подъёма К=0. Поэтому начальная кинетическая энергия равна
К0=П – П0=mgh.
Откуда
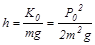 .
.
При распрямлении пружины импульсы, получаемые телами, равны по величине в соответствии с законом сохранения импульса.
Поэтому
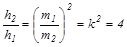 .
.
Задача 24. На горизонтальной поверхности находятся два тела массами m1 и m2 (m1 > m2), между которыми зажата легкая пружина жесткостью k. Сравните пути, пройденные телами после распрямления пружины, S1 и S2,если коэффициенты трения между телами и горизонтальной поверхностью одинаковы и равны µ.
 Решение. Проанализируем физическую ситуацию. Каждое из тел находится под воздействием четырех сил: силы тяжести
Решение. Проанализируем физическую ситуацию. Каждое из тел находится под воздействием четырех сил: силы тяжести 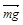 , силы реакции
, силы реакции 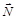 , силы трения покоя Fтр=mN и упругой силы со стороны пружины F = kDx0, где
, силы трения покоя Fтр=mN и упругой силы со стороны пружины F = kDx0, где  – начальная деформация пружины.
– начальная деформация пружины.
Рассмотрим возможные случаи.
1. Если kDx0 < mm2g, то система будет находиться в состоянии покоя, так как упругой силы недостаточно, чтобы сдвинуть тела.
2. Если выполнено условие mm1g > kDx0 > mm2g, то первое тело остаётся в состоянии покоя, второе тело придёт в движение.
3. Если kDx0 > mm1g, в движение придут оба тела.
4. При kDx0 >> mm1g можно пренебречь действием силы трения в процессе распрямления пружины. Начальные импульсы тел после распрямления пружины будут приблизительно одинаковы по величине.
Движение тел после распрямления пружины происходит под действием силы трения. Длину тормозного пути S можно оценить, воспользовавшись теоремой о кинетической энергии
К-К0=Атр=-mmgS.
Откуда для тормозного пути получаем
 ,
,
так как в момент остановки К = 0, а начальная кинетическая энергия тела после растяжения пружины равна
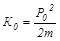 ,
,
где P0 – импульс тела после распрямления пружины.
Таким образом, S ~  при равенстве импульсов и коэффициентов трения. Следовательно, S1<S2 при m1>m2.
при равенстве импульсов и коэффициентов трения. Следовательно, S1<S2 при m1>m2.
Задача 25. Растяжение страховой веревки подчиняется закону Гука, пока относительное растяжение не превышает значения ε0=0,2 (момент обрыва). Оцените минимальную прочность страховой верёвки, при которой альпинист может уцелеть при падении с высоты l. Масса альпиниста равна m=77кг. Сопротивлением воздуха пренебречь.
Решение. При падении альпиниста страховая верёвка удерживает его в положении В. При этом верёвка удлиняется на величину Δl, и общая высота падения альпиниста равна 2l+Δl. В положениях А и В скорость альпиниста равна нулю. При падении потенциальная энергия альпиниста уменьшается, и при этом увеличивается потенциальная энергия удлиняющейся верёвки:

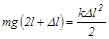 .
.
Выразим коэффициент упругости верёвки k из закона Гука для предельного значения Fпр=kDlпр=ke0l и подставим его в выражение для закона сохранения энергии
 ,
,
где 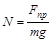 .
.
Поделив последнее уравнение на l2 и учитывая, что 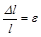 , получаем квадратное уравнение относительно ε:
, получаем квадратное уравнение относительно ε:
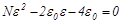 ,
,
положительный корень которого равен
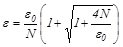 .
.
Относительное удлинение верёвки ε не должно превышать предельного значения ε0.
Приравняв в последнем соотношении ε=ε0, найдем значение для минимальной прочности веревки
 .
.
Задача 26. Шарик массой m=12г, летящий горизонтально со скоростью u0=1,5м/с, сталкивается с покоящимся на горизонтальной поверхности телом массой М=120г. При скорости шарика um=0,85м/с тело сдвигается с места. Определите скорости шарика и тела после столкновения, считая удар упругим. Какое количество теплоты выделяется при столкновении?
Решение. Из условия задачи видно, что на тело действует сила трения. За время столкновения τ импульсы шарика и тела изменятся:
mu- mu0=-Fτ,
МU=(F–Fmp)τ,
где u, U – скорости шарика и тела после столкновения, F – упругая сила, Fmp = μMg – сила трения.
Складывая уравнения, получим
МU+mu-mu0=-μMgτ.
U=(u0 –u)- μgτ. (1)
Время взаимодействия оценим из условия
2mum»Fтрmaxt=Mgmt.
Откуда
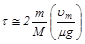 . (2)
. (2)
Подставив (2) в (1), получаем
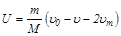 . (3)
. (3)
В уравнении (3) U и u неизвестны. Второе уравнение получим из закона сохранения энергии:
 ,
,
где  .
.
Таким образом, проблема сводится к решению системы уравнений:

Находим
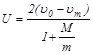 ,
, 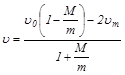 .
.
Количество выделившегося тепла
 .
.
Вычисление:
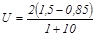 = 0, 12м/с.
= 0, 12м/с.
 =- 1, 4м/с.
=- 1, 4м/с.
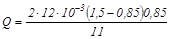 = 1, 2мДж.
= 1, 2мДж.
Предельный переход um=0 (гладкая поверхность):
 ,
,
 , Q=0.
, Q=0.
Если при этом m=M, то U=u0,, u=0.
Задача 27. Шайба плашмя падает на горизонтальную поверхность под углом α=450 к вертикали. Под каким углом к вертикали шайба отскакивает от поверхности, если коэффициент трения между шайбой и поверхностью равен μ=0, 3 и при ударе 10 % её кинетической энергии превращается в теплоту.
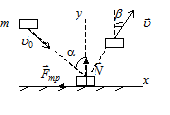 Решение. В процессе столкновения на шайбу действуют сила реакции горизонтальной поверхности
Решение. В процессе столкновения на шайбу действуют сила реакции горизонтальной поверхности 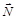 , сила трения скольжения
, сила трения скольжения  и сила тяжести
и сила тяжести 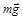 . Запишем основной закон динамики:
. Запишем основной закон динамики:
 .
.
Учитывая, что время столкновения τ мало, и пренебрегая силой тяжести в сравнении с силой реакции (mg<<N), представим основное уравнение динамики в проекциях на координатные оси:
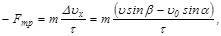
 ,
,
где  .
.
Исключая из скалярных уравнений N, получаем
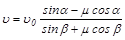 . (1)
. (1)
В этом соотношении две величины u и b неизвестны.
Недостающее соотношение получим из закона сохранения энергии. Выделяющаяся при столкновении теплота равна разности кинетических энергий до и после столкновения:
Q=K0-K.
Так как
 ,
,
скорость шайбы после столкновения равна
 . (2)
. (2)
Из (1) и (2) следует:
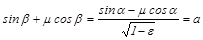 .
.
Представим левую часть последнего уравнения как функцию tgβ:
 .
.
После преобразования получаем квадратное уравнение относительно tgβ
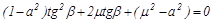 ,
,
положительный корень которого равен
 .
.
Для численных значений в условии задачи находим
а=0,52, tgβ=0236, β=130.
В предельном случае
ε=0, μ=0, β=α.
Угол отражения равен углу падения шайбы при абсолютно упругом столкновении с гладкой поверхностью.
Задача 28. Тело массой m1=0, 12кг, движущееся горизонтально со скоростью u0=15м/с, сталкивается с покоящимся клином массой m2=1, 7кг. Клин может скользить без трения по горизонтальной поверхности. Определите скорость тела u (м/с) и скорость клина U (м/с) после столкновения, если коэффициент трения между телом и клином равен m=0, 5, угол наклона клина к горизонту α=450. Под каким углом β (град) тело отражается от поверхности клина?
Решение. Во время столкновения тело находится под действием сил трения  , реакции клина
, реакции клина 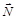 и тяжести
и тяжести 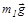 . Считая время столкновения τ малым, представим основное уравнение динамики для тела в импульсной форме:
. Считая время столкновения τ малым, представим основное уравнение динамики для тела в импульсной форме:
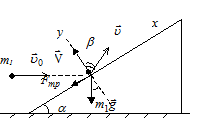
 ,
,
или в проекциях на координатные оси:
 , (1)
, (1)
 , (2)
, (2)
где Fmp=μN.
Из (1) и (2) получаем
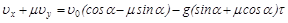 . (3)
. (3)
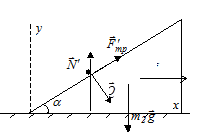 Рассмотрим движение клина. Он во время столкновения находится под действием сил трения
Рассмотрим движение клина. Он во время столкновения находится под действием сил трения  , реакции горизонтальной поверхности
, реакции горизонтальной поверхности  , нормального давления
, нормального давления 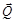 и тяжести
и тяжести  .
.
Воспользуемся основным уравнением динамики для клина в импульсной форме:
 .
.
Представляя векторное уравнение в проекциях на координатные оси и учитывая третий закон Ньютона ( ,
, 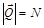 ), получим
), получим
 , (4)
, (4)
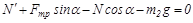 ,
,
где  ,
, 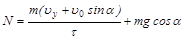 . (5)
. (5)
Из (4) и (5) получаем
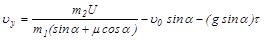 . (6)
. (6)
Для малых τ из (6) и (3) находим
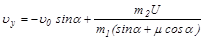 ,
,

Таким образом, скорость тела 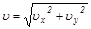 и скорость клина U связаны соотношением:
и скорость клина U связаны соотношением:
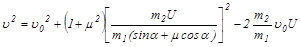 . (7)
. (7)
Дополнительное соотношение, связывающее скорости u и U, получим из закона сохранения энергии:
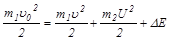 ,
,
где 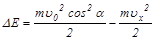 .
.
Подставив значение ux в выражение для ΔЕ, получаем
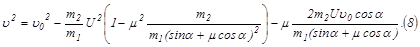 Из (7) и (8) находим
Из (7) и (8) находим
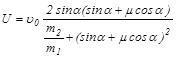 =1,5м/с.
=1,5м/с.
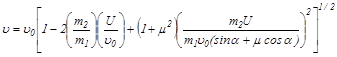 = 9,1м/с. Угол отражения β можно определить из соотношения
= 9,1м/с. Угол отражения β можно определить из соотношения
 .
.
Откуда β=4,90.
Предельные переходы.
1. Идеально гладкий клин (μ=0):
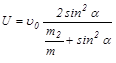 ,
,
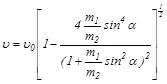 ,
,
 .
.
При α=900 (центральное столкновение)
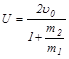 ,
, 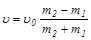 .
.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 8263; Нарушение авторских прав?; Мы поможем в написании вашей работы!