Примеры решения задач 3 страница

Решение. Бусинка движется под действием силы тяжести 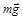, силы реакции 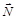и силы трения .

Положение бусинки на стержне будет неоднозначным, так как величина и направление силы трения покоя может меняться от нуля до максимального значения, равного mN.

Крайние положения равновесия бусинки на стержне А и В определяются максимальными значениями сил трения покоя, которые препятствуют смещению бусинки вниз в точке А и вверх в точке В.

Рассмотрим положения равновесия бусинки в точке А. Бусинка неподвижна относительно стержня в точке А, если выполнены условия

Ncosa - F_трsina=mw²r_A,

Nsina + F_трcosa=mg,

где F_тр=mN, r_A=l_Asina (l_A – расстояние от точки О до точки А вдоль стержня).

Откуда для l_A находим

Бусинка удерживается на стержне в точке А силой трения покоя, если угол a удовлетворяет условию

a<arctg(1/m).

Аналогично, рассматривая условие равновесия бусинки на стержне в точке В, находим

Бусинка удерживается на стержне в точке В, если угол a удовлетворяет условию

a>arctg(1/m).

Таким образом, бусинка может находиться в равновесии на стержне в любой точке интервала l_A£l£l_B при условии

arctgm<a<arctg(1/m).

Для численных данных в условии задачи 39⁰<a<51⁰.

Угол наклона стержня a=45⁰ удовлетворяет условию существования равновесия на стержне в положениях, определяющихся неравенством 2,5см<l<20см.

В случае идеально гладкого стержня (m=0) равновесное положение бусинки

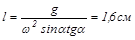
будет неустойчивым.

Бусинка будет скользить вверх или вниз по стержню в результате случайного отклонения, удаляясь от положения неустойчивого равновесия. Устойчивому положению равновесия соответствует l=0.

Задача 37. Горка в форме наклонной поверхности плавно переходит в цилиндрическую поверхность радиусом R=0,53м. С какой максимальной высоты h_m(м) необходимо спустить небольшое тело, чтобы оно смогло преодолеть “мертвую петлю”? Угол наклона горки к горизонту равен a=32⁰, коэффициент трения между телом и горкой m=0,15. Небольшой участок плавного перехода и внутреннюю поверхность цилиндра можно считать гладкими (m=0). Тело начинает двигаться из состояния покоя.

Решение. Вначале выясним, выполняется ли условие скольжения тела по наклонной плоскости горки. Чтобы тело скользило вниз, то должно выполняться условие a>arctgm. В нашем случае это условие выполнимо (убедитесь в этом).

Высоту спуска h необходимо подобрать так, чтобы тело смогло подняться до точки А и не оторвалось от нее.

Рассмотрим условие прохождения точки А. Воспользуемся для анализа основным законом динамики

.

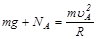Сила реакции N_A определяется скоростью тела в точке А. Минимальную скорость тела в точке А u_Amin, при которой тело проходит критическую точку, найдем с учетом условия N_A=0:

Следовательно, в критической точке механическая энергия тела не может быть меньше

.

Очевидно, величина запаса энергии должна быть такой, чтобы обеспечить надлежащий уровень механической энергии в критической точке и компенсировать потерю механической энергии, связанную с работой силы трения при движении тела по горке:

E=E_A+A,

где E=mgh_m (начальная скорость равна нулю), A=mmgh_mctga.

Из последнего соотношения получаем

Если трением на цилиндрической поверхности пренебречь нельзя, то при равенстве коэффициентов трения на горке и цилиндрической поверхности для минимальной высоты получается

Из полученных соотношений в пределе для идеально гладких поверхностей получается известный результат:

h_m=2,5R=1,3 м.

Точность оценки существенно зависит от принятой модели.

Задача 38. На вершине сферы радиусом R=0,26м находится небольшое тело, которому сообщили начальную скорость u₀=1,2м/с в горизонтальном направлении. Коэффициент трения между телом и поверхностью сферы равен m=0,1. В какой точке тело отрывается от сферы? Чему равна скорость тела в момент отрыва от поверхности сферы? Сопротивлением воздуха пренебречь.

Решение. 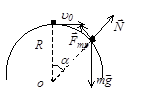В такой постановке задача более близка к реальной действительности, но становится сложной в математическом отношении. Очевидно, при больших значениях коэффициента трения влияние силы трения на характер движения будет существенным, но при малых 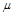(каких?) предположение о гладкости сферы может оказаться вполне приемлемым. Количественную оценку последнему можно дать, только решив предложенную задачу или проведя эксперимент.

Проведем теоретическое исследование поставленной задачи. Тело на сфере находится под действием силы тяжести 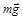, силы реакции 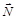и силы трения (см. рисунок).

Для анализа воспользуемся основным уравнением динамики в скалярной форме:

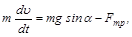
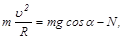
где F_тр=mN.

Из этой системы уравнений после несложных преобразований (см. задачу 33) получим следующее уравнение относительно квадрата скорости тела:

Представим последнее уравнение в обобщенной форме в безразмерных величинах:

,

где 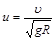- безразмерная скорость.

Его частное решение должно удовлетворять условию a=0, u=u₀, где .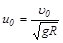

Полученное уравнение является линейным дифференциальным уравнением второго порядка, частное решение которого имеет вид

.

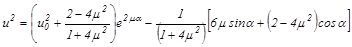Убедитесь самостоятельно в том, что полученное решение в пределе переходит в решение для идеально гладкой сферы.

Для силы реакции сферы получаем

.

Откуда, положив N=0, находим уравнение для полярного угла, соответствующего точке отрыва, :

.

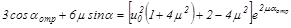Для m=0

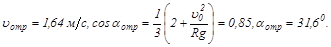
Для m=0,1

Для m=0,5

.

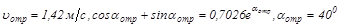Из расчетов видно, что при значениях коэффициента трения m£0,1 расхождение в результатах в сравнении со случаем гладкой сферы (m=0) незначительно (не более 6 %).

Задача 39. Профиль края горизонтального стола скруглен в полуокружность радиусом R=0,55м. Небольшому телу сообщили горизонтальную скорость u₀=3,5м/с. Определите точку отрыва тела на скруглении, если в начальный момент времени тело находилось на расстоянии S=4,2м от начала скругления. Коэффициент трения между телом и горизонтальной поверхностью принять равным m=0,11, а скругление считать гладким.

Решение. Сначала оценим, достигнет ли тело точки А (начало скругления). Начальная кинетическая энергия тела должна быть не меньше работы силы трения на горизонтальном участке пути S.

.

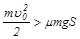Отсюда находим условие для оценки начальной скорости тела:

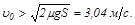
В нашем случае условие выполнено.

В точке А тело будет иметь скорость

.

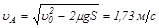Начиная с точки А, тело движется по окружности без трения, если не отрывается в точке А. Запишем основное уравнение динамики для точки А:

.

Из уравнения следует, что тело отрывается в точке А (N_A=0), если его скорость в этой точке будет равна

.

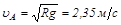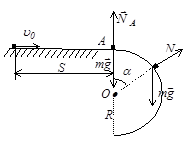В нашем случае точка отрыва лежит ниже точки А.

Исследуем движение тела по гладкому скруглению. В произвольной точке на скруглении тело находится под действием силы тяжести 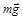и силы реакции 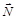(см. рисунок):

.

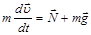Представим основное уравнение динамики в скалярной форме:

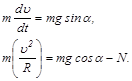
В точке отрыва N=0. Из второго уравнения получаем соотношение, связывающее скорость в точке отрыва u_отр и полярный угол, соответствующий точке отрыва, a_отр:

.

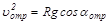Решая первое уравнение (см. задачу 33) при условии, что u(0)=u_A, находим

.

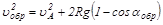Окончательно для определения полярного угла точки отрыва получим

.

Скорость тела в точке отрыва равна

.

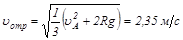В случае гладкой сферы (m=0) при u_А=0 получается известный результат:

.

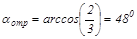Учет силы трения на скруглении усложняет решение. В конечном счет проблема сводится к определению корня трансцендентного уравнения (см. задачу 37).

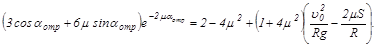
Для данных в условии задачи a _отр=30⁰.

Задачи для самостоятельного решения
(Движение по окружности)

1. На какой максимальный угол можно отклонить шарик, чтобы нить подвеса не оборвалась при прохождении положения равновесия. Нить выдерживает нагрузку в 2mg, где m -масса шарика (60⁰).

2. На нити длиной l=98см подвешен шар массой m₁=1,0кг, радиусом R=4,0 см. В шар попадает горизонтально летящая пуля и застревает в нем. Масса пули m₂=10, скорость пули u₀=400м/с. Оборвется ли нить, если она выдерживает нагрузку в 30Н? (нет).

3. Небольшой груз, подвешенный на нерастяжимой нити длиной l=1,0м, отклонили от положения равновесия на угол 90⁰ и отпустили, сообщив скорость в направлении равновесия, равную 3,0м/с. В каком положении груза нить оборвется, если она выдерживает нагрузку, равную 3mg (m -масса груза)? (46⁰).

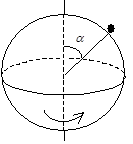4. На сферической поверхности радиусом R=0,5м находится небольшое тело. Коэффициент трения между телом и поверхностью сферы m=0,8. Угол a=30⁰ (см. рисунок). Определите предельную угловую скорость вращения сферы, при которой тело удерживается на поверхности сферы (2,5 рад/с).

5. На внутренней поверхности сферы радиусом R=0,15 м, которая вращается вокруг вертикальной оси, проходящей через центр сферы, находится небольшое тело. С какой предельной угловой скоростью может вращаться сфера, чтобы тело находилось в точке, направление на которую из центра сферы составляет с вертикалью угол в 45⁰? Коэффициент трения между телом и поверхностью сферы равен 0,67 (22рад/с).

6. Метатель посылает молот массой m=6,0кг на расстояние S=60м по траектории, которая обеспечивает наибольшую дальность броска. Оцените максимальную силу, которая действует на метателя при ускорении молота, если разгон ведется по окружности радиусом R=2,0м. Сопротивление воздуха при оценке не учитывать (1,8 кН).

7. Два шарика подвешены на нерастяжимых нитях (см. рисунок), вращаются в одной горизонтальной плоскости по окружностям радиусами R₁ и R₂. Сравните периоды вращения шариков (T₁=T₂).

8. Коэффициент трения покоя между шинами автомобиля и полотном дороги летом больше в N раз, чем зимой. Предельные скорости автомобиля на повороте летом и зимой относятся как N^к. Определите степень к (0,5).

9. Небольшой шарик массой m=55г прикреплен к концу упругой нити, жесткость которой к=43Н/м. Нить с шариком отвели в горизонтальное положение и отпустили. Когда груз проходил положение равновесия, длина нити оказалась равной l=1,1м. Определите силу натяжения нити при прохождении грузом положения равновесия (1,6Н).

10. Небольшое тело начинает скользить с высоты h=1,2м без начальной скорости по наклонному желобу, переходящему в полуокружность радиусом R=55см. Пренебрегая трением, оцените скорость тела в точке отрыва (2,1м/с).

11. Автомобиль движется по выпуклому мосту, имеющему профиль дуги окружности радиусом R=30м. Определите скорость движения автомобиля, если в верхней точке моста сила давления на мост равна ¼mg (m -масса автомобиля) (15м/с).

12. На экваторе некой планеты тела весят в 2 раза меньше, чем на полюсе. Средняя плотность вещества этой планеты равна 3,0г/см³. Чему равны сутки на этой планете? (2,7 часа ).

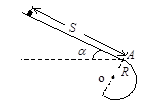13. На каком минимальном расстоянии S(м) от точки А (см.рисунок) необходимо поместить тело, чтобы оно оторвалось от поверхности в этой точке? Угол наклона плоскости, по которой движется тело, равен a=45⁰. Радиус скругления R=0,8 м. Коэффициент трения между телом и плоскостью 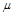= 0,2 (0,35м).

14. Оцените массу нашей Галактики, принимая во внимание, что Солнце находится на краю Галактики на расстоянии ~10⁴ парсек от её центра и имеет орбитальную скорость ~300км/с. 1 парсек@ 3,08×10¹⁶м (~ 4×10 кг).

15. Мотоциклист едет по внутренней поверхности вертикального цилиндра радиусом R=5,8м. Центр тяжести человека и мотоцикла расположен на расстоянии l=0,8м от стенки цилиндра. Коэффициент трения между колесами и стенкой m=0,5. С какой максимальной скоростью может ехать мотоциклист по горизонтальной окружности цилиндра? (10м/с).

16. На твердый стержень, расположенный под углом 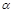= 32⁰ к вертикали, насажен небольшой шарик. Стержень вращается с частотой n=2,1об/с вокруг вертикальной оси. Коэффициент трения между стержнем и шариком равен m=0,34. Оцените интервал расстояний до оси вращения равновесного положения шарика на стержне (4,7см;24см).

17. Наклонная плоскость плавно переходит в цилиндрическую поверхность радиусом R=0,64м. Небольшое тело скользит по наклонной плоскости с высоты h=3,4м без начальной скорости. Угол наклона плоскости к горизонту равен 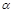=45⁰. Коэффициент трения между телом и плоскостью m=0,57. Небольшой участок плавного перехода и внутреннюю поверхность цилиндра можно считать гладкими (m=0). Определите высоту точки отрыва тела от поверхности цилиндра (1,1м).

18. На вершине сферы радиусом R=0,37м находится небольшое тело, которому сообщили начальную скорость u₀=1,4м/с в горизонтальном направлении. Коэффициент трения между телом и поверхностью сферы равен m=0,35. Определите скорость тела в момент отрыва его от поверхности сферы (2,17м/с).

19. Космическая станция массой 100т вращается на круговой орбите на высоте 600км над поверхностью Земли. Сила трения, действующая на станцию в верхних слоях атмосферы, равна F=-cuⁿ, где u -орбитальная скорость станции. Станция за сутки снижается на Dh=4,3м. Определите значения с и n. Радиус Земли принять равным 6400км (с=6×10 кгс/м², n=3).

20. В результате трения в верхних слоях атмосферы механическая энергия спутника Земли уменьшилась на 4%. Орбита спутника при этом осталась круговой. Определите период обращения спутника, если вначале спутник вращался на высоте 500км над поверхностью Земли. Радиус Земли принять равным 6400км (90мин).

Примеры решения задач
(Поступательное и вращательное движение твердого тела)

Задача 40. Маятник Обербека представляет собой твердое симметрическое тело, вращающееся вокруг собственной оси. Вдоль радиальных спиц маятника можно передвигать одинаковые грузы массой m₀=255г и закреплять их на равном расстоянии R от оси маятника. К шкиву маятника радиусом r=5,9см привязана нить длиной l=1,1м, к концу которой подвешен груз массой m=210г. Момент инерции маятника без грузов m₀ равен J₀=0,013кгм². Определите момент силы трения в оси маятника, если груз m падает с высоты h=l за время t=3,1с. Число спиц n=4. Грузы m₀ закреплены на расстоянии R=12см.

Решение. Маятник вращается под действием момента силы натяжения нити N₂×r и момента силы трения в оси вращения М_тр, а груз m движется поступательно под действием силы тяжести и силы натяжения нити 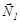. Уравнения движения маховика и груза имеют вид:

N₂r-М_тр=Je, (1)

mg-N₁=ma, (2)

где a=er, N₁=N₂, если нить нерастяжима, J=J₀+nm₀R² – момент инерции маятника относительно оси вращения согласно теореме Штейнера.

Ускорение падения груза m равно

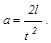
Из системы уравнений (1) и (2) получаем

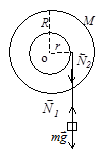Задача 41. Маховик в форме сплошного однородного диска радиусом R=13см и массой М=1,2 кг насажен на горизонтальную ось, проходящую через его центр. К маховику приварен соосный тонкостенный цилиндр радиусом r. Массой цилиндра можно пренебречь. На цилиндр намотан шнур, к свободному концу которого привязан груз массой m=2,5кг. Определите, при каком значении радиуса цилиндра r_m угловое ускорение маховика будет наибольшим. С каким ускорением движется при этом груз m? Трением в оси вращения, сопротивлением воздуха и массой шнура пренебречь.

Решение. В данной связанной системе тел груз m движется поступательно под действием силы тяжести и силы натяжения шнура 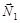, а маховик вращается вокруг неподвижной оси под действием момента силы натяжения шнура N₂r. Уравнения движения маховика и груза имеют вид:

N₂r=J₀e, (1)

mg-N₁=ma, (2)

где J₀=1/2MR² – момент инерции маховика относительно ос вращения.

Из условия невесомости шнура следует, что

N₁=N₂. (3)

Кроме того, если можно пренебречь растяжимостью шнура, то ускорение груза m и касательное ускорение точек обода цилиндра будут равны:

a=a_t=er. (4)

Из уравнений (1) и (2) с учетом условий (3) и (4) получаем для углового ускорения вращения маховика

Как видно, угловое ускорение является функцией радиуса r. Эта зависимость e (r) имеет максимум (убедитесь в этом) при

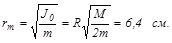
Груз при этом будет падать с ускорением

a=g/2=5,0м/с².

Задача 42. На подвижной призме с углами при основании a=30⁰ и b=45⁰ находится система двух связанных тел массами m₁=1,1кг и m₂=4,2кг. Тела связаны нерастяжимой нитью, перекинутой через блок массой m_б=0,46кг, закрепленной в вершине призмы. Коэффициент трения между телами и гранями призмы равен m=0,5. Как будет двигаться система грузов, если нить не проскальзывает по блоку, а трением в оси блока можно пренебречь.

Решение. Выясним, в какую сторону будет двигаться система грузов – по часовой стрелке или против. Рассмотрим условия вращения системы по часовой стрелке. Первое тело должно подниматься вверх по грани с углом наклона a, а второе – опускаться вниз по грани с углом наклона b. Поэтому должны выполняться условия:

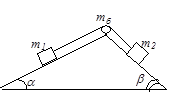F₁- m₁gsina-m m₁gcosa³0,

m₂gsinb-m m₂gcosb-F₂³0,

F₁>F_2,

где F₁, F₂ – силы натяжения нити слева и справа от блока.

Из этих условий получаем соотношение между массами тел, при котором система движется по часовой стрелке:

,

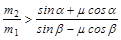если m<tgb.

Аналогично, рассматривая возможное движение системы против часовой стрелки, находим

,если m<tga.

Таким образом, для всех значений m₂/m₁, удовлетворяющих неравенству

система тел покоится на призме.

Для численных данных в условии задачи система движется по часовой стрелке (убедитесь в этом).

Поступательное движение тел по граням призмы и вращение блока описываются системой уравнений динамики:

m₂g(sinb-mcosb)-F₂=m₂a₂,

F₁-m₁g(sina+mcosa)=m₁a₁,

(F₂- F₁)R=J_бe,

где J_б=1/2m_бR² (считая блок однородным диском).

Дополнительные соотношения, связывающие неизвестные величины a₁, a₂, e, определяются условием нерастяжимости нити и отсутствием проскальзывания нити по блоку:

a₁=a₂ =a_t=eR,

где R – радиус блока.

Из системы уравнений динамики находим

Из найденного решения можно получить множество частных решений. Например, при a=b=90⁰, m_б=0 получается известное решение

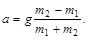
Решение для движения системы против часовой стрелки можно получить перестановкой масс и углов в найденном решении.

Задача 43. Круглое тело раскрутили до угловой скорости w₀(рад/с) и поставили на горизонтальную поверхность. Коэффициент трения между телом и поверхностью равен m.. Оцените время торможения тела t(с), установившуюся скорость качения тела u(м/с), выделяющееся количество теплоты Q(Дж) и длину участка стабилизации качения S(м), если сопротивлением воздуха и трением качения можно пренебречь. Массу m(кг) и радиус R(м) тела считать заданными.

Решение. Проанализируем физическую ситуацию. Раскрученное тело обладает кинетической энергией

где J=CmR² ,С – формпараметр круглого тела.

На горизонтальной поверхности тело находится под действием трех сил – силы тяжести , силы реакции 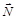и силы трения скольжения . Сила тяжести уравновешена силой реакции, поэтому процесс движения тела будет определяться только силой трения скольжения. В данном случае сила трения выполняет двоякую роль: с одной стороны, она тормозит вращательное движение, с другой – сообщает телу поступательное движение в горизонтальном направлении.

Энергетически это означает, что за счет убыли кинетической энергии вращения растет кинетическая энергия поступательного движения тела и наблюдается диссипация механической энергии.

Движение тела описывается уравнениями динамики

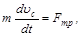(1)

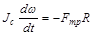(2)

с начальными условиями w(0)=w₀, u_с(0)=0, где F_тр=mmg – сила трения скольжения, J_c=CmR² – момент инерции круглого тела относительно оси, проходящей через центр инерции, u_с - скорость движения центра инерции тела.

Из уравнений (1) и (2) получаем

Дата добавления: 2014-11-25