Основные понятия, соотношения, законы 1 страница

Динамика

Динамика материальной точки

Импульс (количество движения) – векторная мера механического движения частицы:

,

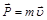где 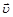– скорость частицы, – “инертная” масса частицы.

Кинетическая энергия – скалярная мера механического движения:

.

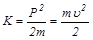Момент импульса относительно точки – векторная мера вращательного движения:

,

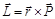где 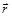– радиус – вектор частицы относительно точки.

Понятие силы и момента силы относительно точки:

,

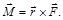
Основное уравнение динамики (второй закон Ньютона):

,

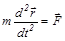где 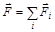– равнодействующая сил, действующих на частицу.

Основное уравнение динамики в проекциях на касательную и нормаль к траектории:

,

,

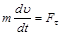где R – радиус кривизны траектории.

Импульс силы, характеризующий действие силы во времени, равен приращению импульса частицы за время действия силы (основной закон динамики в интегральной форме):

.

Работа силы, характеризующая действие силы в пространстве, равна приращению кинетической энергии (теорема о кинетической энергии):

.

Мгновенная мощность силы

.

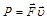Средняя мощность (равна отношению работы, совершаемой за промежуток времени Dt, к этому промежутку)

.

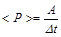Частица в потенциальном поле

Энергия частицы в потенциальном поле сохраняется:

Е=К+П=const,

где П – потенциальная энергия частицы в потенциальном поле.

Потенциальная энергия частицы (тела) в поле тяжести Земли

,

где m – масса частицы, R – радиус Земли, h – высота над поверхностью Земли, – ускорение свободного падения у поверхности Земли.

Для h << R

П=mgh – mgR.

Работа сил поля

A=DK=- DП.

Связь между силой и потенциальной энергией частицы в поле:

, .

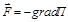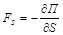Уравнение динамики тела переменной массы:

,

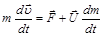где m – переменная масса тела, – скорость отделяемого (присоединяемого) вещества относительно рассматриваемого тела, 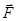– сумма внешних сил.

Динамика системы частиц

Импульс системы частиц

,

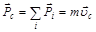где 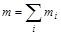– масса системы частиц (закон аддитивности массы), – скорость центра инерции системы частиц.

Уравнение движения центра инерции системы:

,

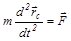где – результирующая внешних сил, 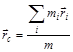– центр инерции системы.

Приращение импульса системы частиц

.

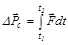Импульс изолированной системы частиц сохраняется:

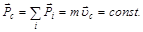
Механическая энергия системы

E=K+П,

где 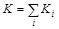– кинетическая энергия системы, 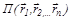– потенциальная энергия системы.

Изменение механической энергии системы

,

где А_в – работа внешних сил, А_д – работа внутренних непотенциальных сил.

Механическая энергия изолированной и консервативной системы сохраняется:

Е=К+П=const, или DК=-DП.

Если система находится во внешнем потенциальном поле, то можно ввести понятие потенциальной энергии во внешнем поле и включить ее в механическую энергию системы. При этом изменение механической энергии системы 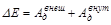, где 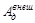– работа внешних непотенциальных сил, – работа внутренних непотенциальных сил.

Момент импульса системы

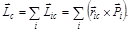
Изменение момента импульса системы

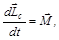
где 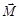– сумма моментов внешних сил относительно центра инерции.

Момент импульса изолированной системы частиц сохраняется: .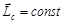

Законы сил

Закон всемирного тяготения:

,

где 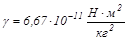– гравитационная постоянная. Закон справедлив для материальных точек и шаров со сферическим распределением массы, где r – расстояние между точками или центрами шаров.

Сила тяжести:

,

где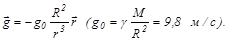

Сила упругих деформаций растяжения-сжатия (закон Гука):

,

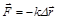где k – коэффициент упругости, 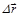– перемещение конца тела.

Максимальная сила трения покоя и сила трения скольжения

,

где m – коэффициент трения, N – сила реакции поверхности.

Сила сопротивления (u < u_зв):

,

где с – коэффициент сопротивления, зависящий от плотности среды, формы и размеров тела.

Сила вязкого трения:

,

где зависит от вязкости среды, формы и размеров тела. Например, для шара (закон Стокса): 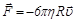, где R – радиус шара, h – вязкость среды.

Динамика вращательного движения тел вокруг

неподвижной оси

Момент инерции тела относительно оси вращения

,

где – момент инерции материальной точки относительно оси вращения (m_i – масса материальной точки, r_i -расстояние от точки до оси вращения).

Момент импульса тела относительно оси вращения

,

где 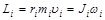– момент импульса материальной точки относительно оси вращения.

Момент силы относительно оси вращения

,

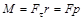где 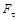– касательная составляющая силы, r – расстояние от точки приложения силы до оси вращения, р – плечо силы.

Основной закон динамики вращательного движения тела относительно неподвижной оси в дифференциальной форме:

,

где 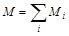– сумма моментов внешних сил.

Основной закон динамики вращательного движения тела относительно неподвижной оси в интегральной форме:

.

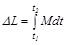Момент импульса замкнутой системы тел, вращающихся вокруг общей оси, сохраняется:

.

Работа момента силы

.

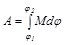Кинетическая энергия вращения

.

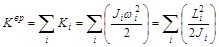Теорема о кинетической энергии:

,

где 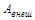– работа внешних сил, – работа внутренних диссипативных сил.

Динамика вращательного движения твердого тела относительно неподвижной оси

Момент импульса твердого тела относительно оси вращения

,

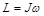где – момент инерции твердого тела относительно оси вращения, w – угловая скорость вращения твердого тела.

Основной закон динамики вращательного движения твердого тела относительно оси вращения:

,

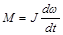где 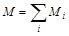– сумма моментов внешних сил относительно оси вращения.

Теорема Штейнера:

,

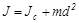где J_c – момент инерции твердого тела относительно оси, проходящей через центр инерции и параллельной данной оси, m – масса тела, d –расстояние между осями.

Момент инерции сплошного цилиндра радиусом R относительно оси цилиндра

.

Момент инерции тонкого стержня длиной l относительно оси, проходящей через его центр и перпендикулярной к стержню,

.

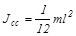Момент инерции шара радиусом R относительно оси, проходящей через центр шара,

.

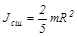Плоское движение твердого тела

Основные уравнения плоского движения твердого тела:

,

,

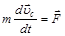где m – масса тела, – скорость центра масс, – сумма внешних сил, J_c – момент инерции тела относительно оси, проходящей через центр инерции, М – сумма моментов внешних сил относительно оси, проходящей через центр инерции.

Кинетическая энергия плоского движения твердого тела

.

Механические колебания

Уравнение гармонических колебаний:

,

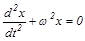где – циклическая частота (k – коэффициент квазиупругой силы, m – масса тела).

Связь циклической частоты с периодом колебаний

.

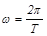Период колебаний тела, подвешенного на пружине,

,

где k – жесткость пружины.

Период колебаний математического маятника

,

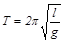где l – длина маятника, g - ускорение силы тяжести.

Период колебаний физического маятника

,

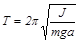где J – момент инерции колеблющегося тела относительно оси колебаний, a – расстояние от оси колебаний до центра тяжести.

Уравнение движения гармонических колебаний

,

где A – амплитуда, j₀ – начальная фаза.

Скорость гармонических колебаний

,

где – амплитудное значение скорости.

Ускорение гармонических колебаний

,

где 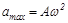– амплитудное значение ускорения.

Уравнение затухающих колебаний

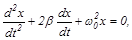
где 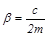коэффициент затухания, 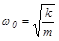– циклическая частота собственных колебаний (с – коэффициент пропорциональности в законе вязкого трения 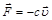, m – масса тела).

Уравнение движения затухающих колебаний (w₀ > b):

,

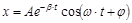где – циклическая частота затухающих колебаний.

Декремент затухания

,

где 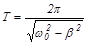– период затухающих колебаний.

Логарифмический декремент затухания

.

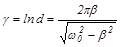Уравнение вынужденных колебаний:

,

где 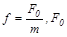– амплитудное значение вынуждающей силы, w – циклическая частота вынуждающей силы.

Уравнение движения вынужденных колебаний в установившемся режиме:

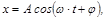
где , .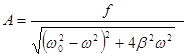

Резонансная частота

.

Резонансная амплитуда

.

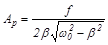Примеры решения задач
(Поступательное движение твердого тела)

Задача 13. Тело движется по горизонтальной поверхности под действием силы 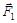или 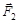(см. рисунок). Сравните ускорения тела а₁ и а₂, если коэффициент трения скольжения между телом и поверхностью равен m.

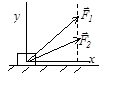Решение. Правильный ответ а₁ > а₂. Объяснение связано с пониманием закона силы трения скольжения , где N – величина силы реакции или силы нормального давления. В рассматриваемом случае сила нормального давления меньше силы тяжести на величину проекции силы F на вертикальное направление:

N=mg–Fsina,

где a – где угол между силой и горизонтальным направлением. Из рисунка видно, что горизонтальные составляющие сил 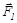и 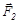одинаковы, а сила трения F_тр2 больше силы трения F_тр1, так как N₂ > N₁. Поэтому а₁ > а₂, как следствие второго закона Ньютона.

Исследуем детально движение тела по горизонтальной поверхности под действием силы, направленной под углом a к горизонту.

Тело будет двигаться с ускорением, если горизонтальная составляющая силы больше силы трения скольжения:

Fcosa>m(mg-Fsina).

Откуда для величины силы F находим

.

Ускорение тела равно

.

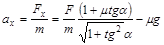Зависимость а_х(tga) имеет максимум при tga_m=m:

.

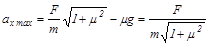Убедитесь в этом, исследуя зависимость а_х(tga) на экстремум.

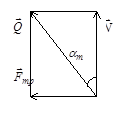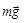Рассматриваемая задача допускает графическое решение. Тело находится под действием силы , силы тяжести , силы реакции 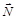и силы трения . Равнодействующую силы представим как сумму

,

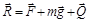где сила 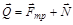направлена под углом a_m к вертикали, так как 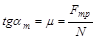в соответствии с законом трения скольжения. Запишем основное уравнение динамики в виде

.

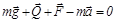Представим графически эту сумму векторов.

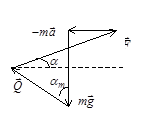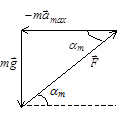Если, не меняя модуля силы , увеличивать угол a, то модуль силы 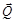будет уменьшаться, а модуль вектора увеличивается и принимает максимальное значение при угле a =a_m, когда сила Q становится равной нулю.

Из векторного треугольника сил находим

.

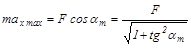Откуда получаем

.

Задача 14. По наклонной плоскости, образующей угол a = 15⁰ с горизонтом, втаскивают с помощью нити груз массой m = 2, 6кг. Коэффициент трения между грузом и плоскостью равен m = 0, 63. Определите минимальную силу F_min, которую необходимо приложить к нити, чтобы втаскивать груз. Чему равен угол b между нитью и наклонной плоскостью при этом?

Для решения задачи воспользуемся основным законом динамики:

.

Представим векторное уравнение в скалярной форме:

,

,

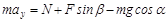где F_тр=mN.

Одно из условий минимальности силы тяги: тело должно двигаться равномерно, не отрываясь от плоскости. Положив а_х = а_у = 0, для силы тяги находим

.

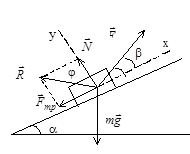
Сила тяги зависит от угла b. При некотором значении угла b_m знаменатель в выражении для силы тяги становится максимальным, а сила тяги при этом принимает минимальное значение. Исследуя знаменатель на экстремум, получаем

b_m=arctgm=32⁰.

Подставив b_m в выражение для силы тяги, находим

=19Н.

В частном случае (a=0) (груз находится на горизонтальной поверхности)

.

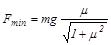Самостоятельно исследуйте зависимость b_m и F_min от коэффициента трения m.

Рассмотрим графическое решение этой задачи. Условие равномерного перемещения груза по наклонной плоскости:

,

или иначе

,

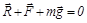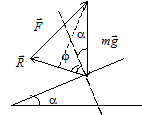где 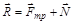– равнодействующая сил трения и реакции плоскости. Вектор силы 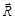составляет угол j с нормалью к поверхности, так как между углом j и коэффициентом трения m имеет место связь:

,

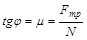в соответствии с законом трения скольжения.

Построим векторный треугольник сил. Вектор силы тяжести направлен вертикально вниз, и длина его известна. Через конец вектора 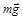проведем прямую, составляющую угол a + j с вертикалью. На этой прямой отложим силу 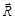, совмещая ее начало с концом вектора 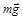. Так как модуль силы 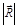нам неизвестен, длину этого вектора выберем произвольно (см. рисунок). В соответствии с векторной суммой сила должна замыкать векторный треугольник сил. Из рисунка видно, что модуль силы 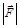будет иметь наименьшую величину, если сила перпендикулярна силе 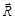. Откуда следует, что сила 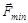направлена под углом j к наклонной плоскости (убедитесь в этом). Таким образом,

b=j=arctgm,

.

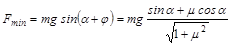Задача 15. Два тела соскальзывают с одинаковой высоты h по наклонной плоскости с углом наклона к горизонту a без начальной скорости. Сравните скорости тел в конце спуска u₁ и u₂ и время соскальзывания t₁ и t₂, если m₁ > m₂, акоэффициент трения m₁ < m₂.

Решение. Правильный ответ: u₁ > u₂, t₁ < t₂.

Для обоснования воспользуемся методом анализа размерностей. Выделим величины, определяющие физический процесс: h (м) – высота, a (град) – угол наклона плоскости, m – коэффициент трения между телом и плоскостью, m (кг) – масса тела, g (м/с²) – ускорение силы тяжести.

Единственная комбинация физических величин, дающая размерность времени – это .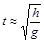

По методу анализа размерностей можно утверждать, что время спуска равно

,

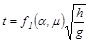где f₁ (a, m) – функция a и m.

Время спуска не зависит от массы тела.

При оценке скорости в конце спуска единственно возможной комбинацией физических величин, дающих размерность скорости, является .

Можно утверждать, что скорость в конце спуска

,

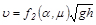где f₂ (a,m)–функция угла a и коэффициента трения m.

Скорость в конце спуска также не зависит от массы. Таким образом, при равенстве коэффициентов трения или отсутствии трения скорости тел и времена их соскальзывания будут одинаковыми. Если m₁¹m₂, определенного вывода сделать нельзя. Хотя интуиция подсказывает, что при m₁<m₂ будут выполняться условия u₁>u₂, t₁<t₂.

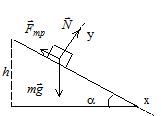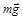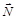Рассмотрим динамическое решение поставленной проблемы. Проанализируем физическую ситуацию. На тело, находящееся на наклонной плоскости, действуют сила тяжести , сила трения и сила реакции . Сопротивлением воздуха, силой Архимеда можно пренебречь (поясните почему).

Если сумма сил

,

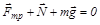Дата добавления: 2014-11-25