
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач 4 страница
|
|
|
|

Скорость скольжения точки соприкосновения тела с поверхностью равна, очевидно, разности линейной скорости точек поверхности круглого тела и скорости поступательного движения тела:
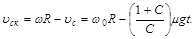
К моменту времени
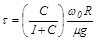
скорость скольжения становится равной нулю и наступает режим чистого качения.
В режиме чистого качения выполняется равенство
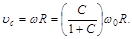
Длина участка стабилизации качения равна
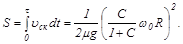
Количество выделяющейся теплоты можно определить, используя закон сохранения энергии или вычислив работу момента силы трения:
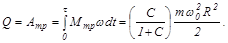
Отметим, что скорость установившегося поступательного движения uс и выделившееся количество теплоты Q не зависят от величины коэффициента трения скольжения m.
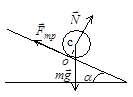 Задача 44. По наклонной плоскости катится круглое тело без скольжения. Плоскость наклонена к горизонту под углом a. Пренебрегая трением качения и сопротивлением воздуха, определите ускорение скатывающегося тела. При каких значениях коэффициента трения m возможно качение без скольжения?
Задача 44. По наклонной плоскости катится круглое тело без скольжения. Плоскость наклонена к горизонту под углом a. Пренебрегая трением качения и сопротивлением воздуха, определите ускорение скатывающегося тела. При каких значениях коэффициента трения m возможно качение без скольжения?
Решение. Рассмотрим энергетическое решение. Так как тело катится без скольжения, а сопротивлением воздуха и трением качения можно пренебречь, то при движении тела сохраняется его механическая энергия. Вначале тело покоится, и его механическая энергия равна потенциальной энергии mgh, а после скатывания механическая энергия равна сумме кинетической энергии поступательного движения и кинетической энергии вращения:
 (1)
(1)
где Jc=CmR2 – момент инерции круглого тела относительно оси, проходящей через центр инерции, m – масса тела (С – формпараметр), uс –скорость центра инерции тела, w – угловая скорость вращения тела (R –радиус круглого тела).
Так как тело катится без скольжения, скорость центра инерции uс и угловая скорость вращения тела w связаны соотношением uс=wR (см. задачу 43).
Из уравнения (1) для скорости центра инерции тела uс после скатывания находим
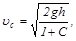 (2)
(2)
где h – высота, с которой скатывается тело.
Центр инерции тела движется с ускорением
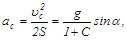 (3)
(3)
так как S=h/sina, uс(0)=0.
Вопрос о значении величины коэффициента трения m энергетически не решается.
Рассмотрим динамическое решение задачи. На тело действует сила тяжести  , сила реакции
, сила реакции 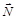 и сила трения покоя
и сила трения покоя  (см. рисунок). Под действием этих сил тело вращается и двигается поступательно согласно уравнениям динамики:
(см. рисунок). Под действием этих сил тело вращается и двигается поступательно согласно уравнениям динамики:
 (4)
(4)
 (5)
(5)
Исключая из системы уравнений (4) и (5) силу трения с учетом, что uс=wR и Jc=CmR2, получаем формулу для расчета ускорения центра инерции тела (3).
Рассмотрим вопрос об оценке значения коэффициента трения m.
Выразим из системы уравнений (4) и (5) силу трения
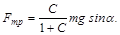
Сила трения покоя ограничена максимальным значением
Fтрmax=mN=mmgsina.
Из условия Fтр£Fтрmax получаем соотношение, ограничивающее значение коэффициента трения

Качение без скольжения для заданного значения коэффициента трения m возможно для углов наклона a, удовлетворяющих условию
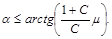
Задача 45. Круглое тело радиусом r катится без скольжения по наклонной плоскости, которая плавно переходит в цилиндрическую поверхность радиусом R. С какой минимальной высоты необходимо скатить тело, чтобы оно могло преодолеть препятствие в форме “мертвой петли“? Сопротивлением воздуха и трением качения пренебречь.
Решение. Скорость центра инерции круглого тела в точке А

(см. задачу 44).
Движение по внутренней поверхности цилиндра описывается системой уравнений динамики:
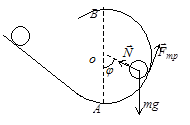
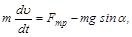 (1)
(1)
 (2)
(2)
 (3)
(3)
где Jc=Cmr2 – момент инерции круглого тела относительно собственной оси вращения (m – масса тела, С – формпараметр).
К уравнениям (1)-(3) следует добавить соотношение, связывающее скорость поступательного движения тела и угловую скорость вращения при отсутствии скольжения:
u=wR. (4)
Из уравнений (1) и (3) с учетом (4) находим уравнение для скорости поступательного движения тела
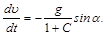
Проинтегрируем последнее уравнение (см. задачу 32), учитывая, что u=uA при j=0.
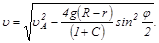 (5)
(5)
Проанализируем физическую ситуацию в критической точке В. Тело должно дойти до точки В и не оторваться от нее.
Из основного уравнения динамики (2) для точки В
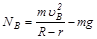
видно, что сила реакции NB определяется скоростью поступательного движения в этой точке. Тело не отрывается в точке В, если NB>0. Минимальную скорость тела в точке В, при которой оно не отрывается от данной точке, оценим, положив NB=0:
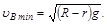 (6)
(6)
Из формулы (5) для минимальной высоты спуска получаем

Этот же результат можно получить из энергетических соображений (убедитесь в этом).
Задача 46. Профиль края горизонтального стола скруглен в полуокружность радиусом R. Круглое тело радиусом r катится по столу без скольжения со скоростью u0. Пренебрегая трением качения и сопротивлением воздуха, определите место отрыва тела от поверхности стола и скорость тела в момент отрыва.
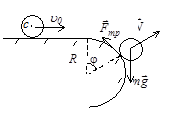 Решение. При движении тела по горизонтальной поверхности стола скорость поступательного движения и угловая скорость вращения w=u0/r не изменяются.
Решение. При движении тела по горизонтальной поверхности стола скорость поступательного движения и угловая скорость вращения w=u0/r не изменяются.
Движение тела по скруглению описывается уравнениями динамики:
 (1)
(1)
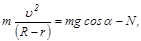 (2)
(2)
 (3)
(3)
где Jc=Cmr2, uc=wr (см. задачи 44, 45).
Решая систему уравнений (1) – (3) с учетом начального условия u=u0 при j=0, находим

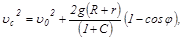
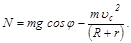
Скорость поступательного движения тела uc увеличивается с ростом полярного угла j, а сила реакции N уменьшается. В точке отрыва N=0. Отсюда получаем соотношение для определения полярного угла, соответствующего точке отрыва:
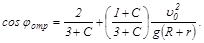
Скорость поступательного движения тела в момент отрыва равна
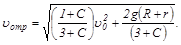
Полученные выражения для joтр и uoтр содержат множество частных случаев (убедитесь в этом).
Интерес представляет проверка предположения о качении без скольжения. Такое качение возможно, если сила трения покоя не превосходит в любой точке максимальной силы трения покоя:
Fтр£mN.
Проведите самостоятельно этот анализ.
Задача 47. Человек, масса которого m1=65кг, переходит с края вращающейся платформы в ее середину. Считая платформу однородным кругом, а человека материальной точкой, оцените изменения кинетической энергии системы. Масса и радиус платформы соответственно равны m2=210 кг, R=2,1м. Начальная угловая скорость вращения системы равна w0=2,3рад/с. Трением в оси платформы и сопротивлением воздуха пренебречь.
Решение. Вопрос: “Будет ли изменяться кинетическая энергия системы?”
Для указанных в условии задачи приближениях систему платформа – человек можно считать изолированной. Поэтому при переходе человека в центр платформы будет сохраняться момент импульса системы относительно оси вращения платформы:
Jw=J0w0,
где J0=J(1+2m1/m2), J=0,5m2R2 – момент инерции платформы относительно собственной оси вращения, w -угловая скорость вращения системы после перехода человека в центр платформы.
Кинетическая же энергия системы при этом не сохраняется. Чтобы сохранялась механическая энергия, одного требования изолированности системы недостаточно. Система взаимодействующих тел должна быть еще и консервативной.
Консервативна ли наша система? Человек имеет возможность передвигаться относительно платформы только благодаря наличию силы трения. Сила трения покоя позволяет мышечной энергии человека превращаться в кинетическую энергию вращения. Наша система неконсервативная. Кинетическая энергия системы возрастает за счет биоэнергии человека. При переходе в центр платформы человек за счет силы энергии покоя “раскручивает” платформу.
Приращение кинетической энергии можно найти, вычислив работу, связанную с переходом человека в центр платформы, или как разницу кинетических энергий системы:
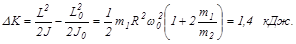
Здесь учтено, что L=L0=J0w0 .
Отметим, что человек может передвигаться по платформе, если коэффициент трения удовлетворяет условию m³w02R/g.
Задача 48. На краю вращающейся платформы находится шайба массой m1=0,21кг. К шайбе одним концом привязана нерастяжимая нить, другой конец которой пропущен через небольшое отверстие в центре платформы. С помощью нити шайбу перемещают в центр платформы. Коэффициент трения между шайбой и платформой равен m=0,4. Оцените работу, затраченную на перемещение шайбы, пренебрегая ее размерами, трением в оси платформы и сопротивлением воздуха. Радиус и масса платформы соответственно равны R=0,57м, m2=5,6кг.
Решение. Хотя рассматриваемая система не является изолированной, тем не менее к ней можно применить закон сохранения момента импульса, так как момент силы натяжения нити относительно оси вращения равен нулю. Поэтому можно записать
Jw=J0w0,
где J0=J(1+2 m1/m2), J=0,5m2R2.
Кинетическая энергия системы при этом возрастает на величину (см. задачу 47)
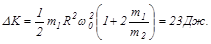
Работа по перемещению шайбы равна сумме приращения кинетической энергии системы и работы силы трения:
A=DK+mmgR=23,5Дж.
Эту же работу можно вычислить непосредственно по формуле работы:
 ,
,
где F=mm1g+ m1w2x – сила, приложенная к нити (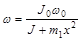 – угловая скорость вращения системы).
– угловая скорость вращения системы).
Задача 49. Человек идет по краю круглой платформы и возвращается в исходную точку. Считая человека точкой, а платформу однородным диском, оцените, на какой угол повернется платформа. Масса человека и платформы соответственно равны m1=75кг, m2=150кг. Трением в оси платформы и сопротивлением воздуха пренебречь.
Решение. При передвижении человека по краю платформы сама платформа с человеком будет вращаться относительно Земли в противоположную сторону движения человека относительно платформы. Для простоты предположим, что человек движется по краю платформы равномерно с угловой скоростью w/ относительно платформы. При этом платформа будет вращаться относительно Земли с угловой скоростью wпл, а человек – с угловой скоростью, равной сумме
w=w/+wпл.
Для определения угла поворота платформы воспользуемся законом сохранения момента импульса:
Jw+J плwпл=0,
где J=m1R2, J пл =0,5m2R2 – моменты инерции человека и платформы.
Откуда для угловой скорости вращения платформы получаем
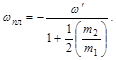
Умножив последнее соотношение на время движения, для угла поворота платформы находим

Знак “ – “ указывает на то, что платформа поворачивается в обратную сторону движения человека по краю платформы.
Угол поворота не зависит от характера движения человека по краю платформы.
Задача 50. Однородный стержень массой m=250г и длиной l=1,2м подвешен за один из концов. Небольшое тело массой m0=120г движется горизонтально со скоростью u0=4,2м/с, сталкивается так, что стержень после столкновения отклоняется на максимально возможный угол. Определите место столкновения тела со стержнем (расстояние от точки подвеса до точки столкновения) и угол отклонения стержня, считая столкновение абсолютно упругим, пренебрегая сопротивлением воздуха и трением в оси.
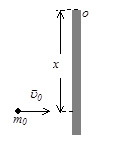 Решение. Воспользуемся законом сохранения момента импульса и механической энергии
Решение. Воспользуемся законом сохранения момента импульса и механической энергии
P0x=L+Px, (1)
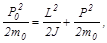 (2)
(2)
где J=(1/3)ml2 – момент инерции стержня относительно точки подвеса, P0=m0u0, P=m0u – импульсы тела до и после столкновения, L – момент импульса стержня после столкновения.
Из уравнений (1) и (2) для неизвестных P и L находим
 (3)
(3)
 (4)
(4)
Как видно, значения P и L зависят от координаты места столкновения. Функция L(x) имеет максимум. Из условия экстремума 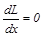 получаем
получаем

Максимальный момент импульса, который получает стержень при столкновении, равен

При этом импульс тела после столкновения равен нулю (убедитесь в этом).
Отклонение стержня в однородном поле тяжести Земли после столкновения можно оценить, решая динамическую задачу или используя закон сохранения механической энергии.
Для расчета угла отклонения стержня получается следующее соотношение:
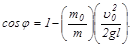
После вычислений получаем xm=1,0 м, j=730.
Задачи для самостоятельного решения
(Поступательное и вращательное движения твердого тела)
1. Маховик, масса которого m=5,2кг распределена по ободу, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 720об/мин. При торможении маховик останавливается через 20с. Определите тормозящий момент, если радиус маховика равен 36см (2,5Нм).
2. На однородный цилиндр массой 5,1кг намотана нерастяжимая нить, к концу которой прикреплен груз массы 0,25кг. В момент времени t=0 система пришла в движение. Определите кинетическую энергию всей системы к моменту времени 3,3с (2Дж).
3. На неподвижный блок намотана нерастяжимая нить, к концу которой прикреплен груз массой 1,7кг. Определите, с каким ускорением будет падать груз, если масса блока равна 2,2кг. Блок считать однородным диском. Сопротивлением воздуха и трением в оси блока пренебречь (6,1м/с2).
4. На неподвижный блок намотана нерастяжимая нить, к концам которой прикреплены грузы массами 1,6кг и 1,2кг. Определите кинетическую энергию системы через 1,8с после начала движения. Масса блока 3,2кг. Блок считать однородным диском. Нить не проскальзывает по блоку. Сопротивлением воздуха и трением в оси пренебречь (15Дж).
5. На неподвижный блок, масса которого равна 25кг, намотана веревка. На веревке висит обезьяна, которая пытается взобраться по ней вверх. С каким ускорением движется веревка, если обезьяна все время остается на одной и той же высоте от пола? Масса обезьяны 5,0кг. Трением в оси блока и массой веревки можно пренебречь (4,0м/с2).
 6. Система тел (см. рисунок) движется с ускорением 1,4м/с2,массы грузов m2=2,3кг, mб=1,6кг, коэффициент трения m=0,2. Нить нерастяжима и не проскальзывает по блоку. Пренебрегая сопротивлением воздуха и трением в оси блока, определите массу m1. Блок считать однородным диском (1,0кг).
6. Система тел (см. рисунок) движется с ускорением 1,4м/с2,массы грузов m2=2,3кг, mб=1,6кг, коэффициент трения m=0,2. Нить нерастяжима и не проскальзывает по блоку. Пренебрегая сопротивлением воздуха и трением в оси блока, определите массу m1. Блок считать однородным диском (1,0кг).
 7. Связанная система состоит из трех тел (см. рисунок): неподвижного блока массой m2=1,8кг, подвижного блока массой m3=2,0кг и груза массой m1=1,5кг. Определите, с каким ускорением падает груз, если нить нерастяжима и не проскальзывает по блокам (1,6м/с2).
7. Связанная система состоит из трех тел (см. рисунок): неподвижного блока массой m2=1,8кг, подвижного блока массой m3=2,0кг и груза массой m1=1,5кг. Определите, с каким ускорением падает груз, если нить нерастяжима и не проскальзывает по блокам (1,6м/с2).
8. Хоккейную шайбу раскрутили до угловой скорости 31рад/с и положили плашмя на лед. Определите время торможения шайбы, если масса и радиус шайбы соответственно равны 0,21кг и 3,2см. Коэффициент трения между шайбой и льдом равен 0,13 (0,57с).
9. Шар, вращающийся вокруг собственной оси с частотой 10об/с, поставили на горизонтальную поверхность. Определите угловую скорость качения шара и долю ее начальной кинетической энергии, которая превращается в теплоту (18 рад/с, 71%).
10. Полый тонкостенный цилиндр, вращающийся с угловой скоростью 15рад/с, поставили на горизонтальную поверхность. За какое время цилиндр пройдет расстояние 5,7м, если его радиус равен 12см, а коэффициент трения между цилиндром и горизонтальной поверхностью равен 0,25 ( 6, 6с).
11. Горизонтальная поверхность плавно переходит в плоскую горку с углом наклона a=250 к горизонту. Однородный цилиндр, вращающийся с угловой скоростью 45рад/с, поставили на горизонтальную поверхность вдали от подножия горки. Определите, на какую высоту вкатится цилиндр, если коэффициент трения между цилиндром и поверхностью всюду равен 0,2. Радиус цилиндра равен 13см. Трением качения и сопротивлением воздуха пренебречь(29 см).
12. Однородный шар спускается по наклонной плоскости с высоты 1,5м. Угол наклона плоскости к горизонту равен 330. Коэффициент трения между шаром и плоскостью всюду, включая горизонтальную поверхность, равен 0,15. Определите установившуюся скорость качения шара по горизонтальной поверхности, если трением качения и сопротивлением воздуха можно пренебречь(4,5м/с).
13. Однородный цилиндр движется по наклонной плоскости с некоторой высоты без начальной скорости. Плоскость наклонена к горизонту под углом 260. Коэффициент трения между телом и плоскостью равен 0,1. Определите отношение кинетической энергии в конце спуска к начальному значению потенциальной энергии тела. Трением качения и сопротивлением воздуха пренебречь (0,9).
14. С какой минимальной высоты необходимо скатить шарик радиусом r=1,1см, чтобы он смог преодолеть барьер в форме “мертвой петли” радиусом R=13см? Шарик катится без скольжения. Сопротивлением воздуха и трением качения пренебречь(33см).
15. Полый тонкостенный цилиндр катится по горизонтальной поверхности, которая плавно переходит в цилиндрическую, без скольжения. При какой минимальной скорости поступательного движения цилиндр прокатится по цилиндрической поверхности, не выпадая, если радиус цилиндрической поверхности равен 41см, а радиус полого цилиндра 2,0см. Трением качения и сопротивлением воздуха пренебречь (3,4м/с).
16. Наклонная плоскость плавно переходит в цилиндрическую поверхность радиусом R=1,2м. Шарик скатывается без скольжения по наклонной плоскости с высоты 2,5м без начальной скорости. Определите высоту точки отрыва шарика от поверхности цилиндра. Радиус шарика равен 0,15м. Трением качения и сопротивлением воздуха пренебречь (1,9м).
17. Диск катится без скольжения по наклонной плоскости с углом наклона к горизонту 270, плавно переходящей в цилиндрическую поверхность радиусом кривизны 25см. Определите минимальную высоту, с которой необходимо скатить диск, чтобы он оторвался от поверхности на линии перехода наклонной плоскости в цилиндрическую поверхность. Радиус диска равен 5см (0,2м).
18. Шар скатывается без скольжения с вершины сферы радиусом 0,50м с начальной скоростью 1,0м/с. Определите полярный угол, соответствующий месту отрыва шарика от сферической поверхности, если сопротивлением воздуха и трением качения можно пренебречь. Радиус шара 10см (490).
19. Шар скатывается без скольжения по наклонной плоскости, которая плавно переходит в цилиндрическую поверхность радиусом R=1,5м. Радиус шара r=11см. Шар скатывается с высоты h=2,9м без начальной скорости. Определите координату точки отрыва шара от поверхности цилиндра (полярный угол)(1300).
20. На однородный стержень, подвешенный за один из концов, попадает горизонтально летящее тело и прилипает к нему. Определите, на какой угол отклоняется стержень от вертикального положения. Длина и масса стержня соответственно равны 0,51см, 980 г. Масса тела 12г. Расстояние от точки подвеса до линии движения тела равно 34см. Скорость тела до столкновения 30м/с (150).
21. Шар массой 2,1кг подвешен на легком стержне. В шар попадает горизонтально летящая пуля массой 9,0г и застревает в середине шара. Определите скорость пули, если система отклонилась от положения равновесия на угол 400. Длина стержня и радиус шара соответственно равны 6,5см, 35см. Сопротивлением воздуха и трением в оси подвеса пренебречь (520 м/с).
22. Период вращения Солнца вокруг собственной оси равен 27 земным суткам. Солнце представляет собой водородную звезду. После того как полностью выгорит водород, Солнце испытает гравитационный коллапс. Оцените радиус Солнца, прежде чем оно разлетится на части. Масса Солнца 2,0×1030 кг, радиус Солнца 7,0×108 (14км).
Примеры решения задач
(Колебательное движение)
Задача 51. Максимальная частота колебаний физического маятника массой m=2,3кг равна nmax=1,3Гц. Определите момент инерции маятника относительно оси, проходящей через ее центр инерции.
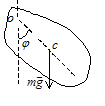 Решение. Маятник совершает вращательное колебательное движение относительно оси качания под действием момента силы тяжести
Решение. Маятник совершает вращательное колебательное движение относительно оси качания под действием момента силы тяжести
Jo 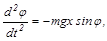
где x=ОС, J0=Jc+mx2, Jc – момент инерции маятника относительно оси, проходящей через центр инерции С, m – масса маятника.
В таком приближение мы пренебрегаем сопротивлением воздуха и трением в оси качания маятника.
При малых углах отклонения маятник совершает гармоническое колебательное движение с угловой частотой
w= 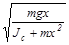 .
.
Зависимость угловой частоты от положения оси качания w(x) имеет максимум при
хm=  .
.
Максимальная угловая частота равна
wmax= 
Откуда находим
Jc=  .
.
Физический маятник применяется для измерения ускорения свободного падения.
Задача 52. По внутренней поверхности цилиндра радиусом R катается круглое тело без проскальзывания. Определите период малых колебаний тела около положения равновесия. Радиус круглого тела равен r. Сопротивлением воздуха и трением качения пренебречь.
Решение. Рассмотрим динамическое решение задачи.
 Поступательное и вращательное движения тела под действием сил тяжести, реакции и трения (см. рисунок) описываются основными уравнениями динамики твердого тела
Поступательное и вращательное движения тела под действием сил тяжести, реакции и трения (см. рисунок) описываются основными уравнениями динамики твердого тела
Fтр-mgsin 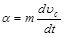 , (1)
, (1)
-Fтр×r=Jc 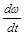 , (2)
, (2)
где Jc=cmr2 – момент инерции круглого тела относительно собственной оси вращения.
Из уравнений (1) и (2), учитывая, что uс=wr (отсутствие проскальзывания), для ускорения поступательного движения тела получаем следующее уравнение:
 .
.
Откуда при малых углах 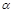 для смещения S=(R-r)
для смещения S=(R-r) 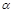 находим
находим
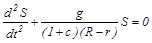 .
.
Таким образом, смещение S(t) описывается гармонической функцией с угловой частотой
w= 
и периодом колебаний
T=2П 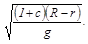
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 10520; Нарушение авторских прав?; Мы поможем в написании вашей работы!