Пример решения задачи 2.2

Условие. Точка М движется по ободу диска радиусом R=20 см согласно закону s = АМ = 6 t sin(pt/3). Диск вращается вокруг неподвижной оси О₁О₂, лежащей в плоскости диска, в направлении, указанном стрелкой, с постоянной

угловой скоростью w=0,5 рад/с. Определить абсолютную скорость точки М в момент времени t ₁ =5 с (рис.2.4).

Рис. 2.4

Решение. В данной задаче относительное движение точки – движение по ободу диска относительной системы отсчета, связанной с диском; переносное движение – вращение вместе с диском вокруг неподвижной оси; абсолютное движение – движение точки относительно неподвижной оси.

Определим параметры относительного движения точки:

а) положение точки М в заданный момент времени t=5 с:

М

Знак минус означает, что точка М в рассматриваемый момент времени находится в области отрицательных значений дуговой координаты s;

б) определим центральный угол a и отрезок MN:

в) найдем проекцию относительной скорости точки М на касательную в данный момент времени (рис. 2.5).

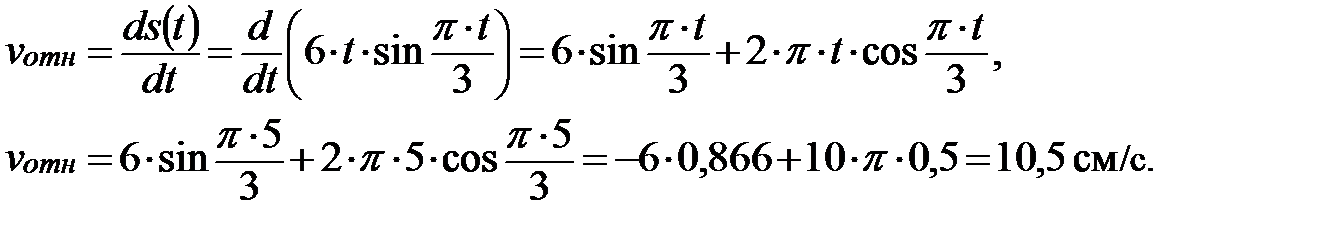
  Рис. 2.5

Определим модуль переносной скорости точки М как вращательной скорости той точки диска, где в данное мгновение находится точка М

.

М

Вектор переносной скорости перпендикулярен плоскости диска и направлен в сторону его вращения.

Модуль абсолютной скорости точки М (рис. 2.5.) найдем по формуле:

Вектор абсолютной скорости направлен по диагонали прямоугольника, построенного на относительной и переносной скоростях как сторонах.

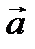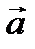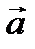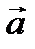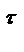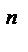Абсолютное ускорение точки М равно (рис. 2.6) геометрической сумме относительного _отн, переносного _пер и кориолисова _кор ускорений: _абс = _отн + _пер + _кор, или с учетом условий задачи в развернутом виде _абс = _отн + _отн + 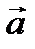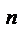_пер + _кор

где при t₁=5с касательное ускорение в относительном движении:

;

нормальное ускорение в относительном движении:

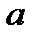
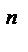_отн = ;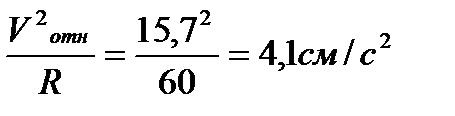

нормальное ускорение в переносном движении:

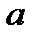
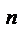_пер = ;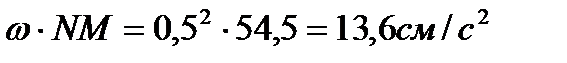

кориолисово ускорение:

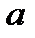_кор = .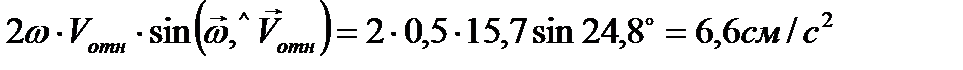

Положительный знак 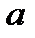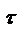_отн показывает, что вектор 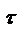_отн направлен в сторону положительных значений S; вектор 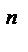_отн направлен по нормали к траектории движения точки в относительном движении, т.е. по нормали к окружности радиусом MN к её центру, вектор _кор направлен согласно правилу векторного произведения векторов и _отн (рис. 2.6)

Модуль абсолютного ускорения точки М находим способом проекции на оси х, у и z (рис. 2.6):

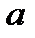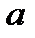
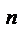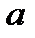
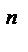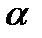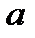
_{абс x} = _пер + _отн cos - 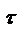_отн sin 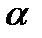=13,6 + 4,1cos 24,8 – - sin 24,8 = 5,37 см/с²

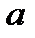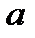
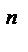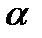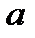
_{абс y} = - _отн sin - 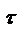_отн cos 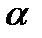= 4,1sin 24,8 – 28,5cos24,8 = = -27,6 см/с² 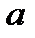_{абс z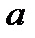} = _кор = 6,6 см/с²

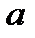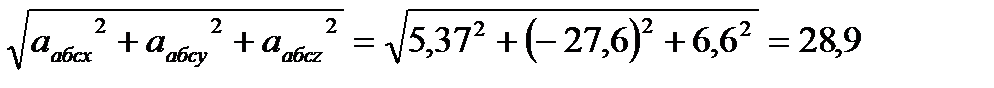_абс = см/с²

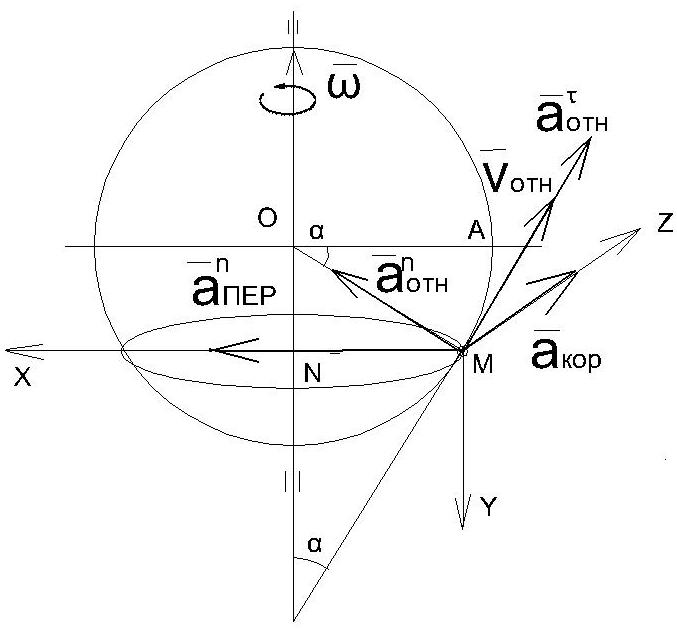
Рис.2.6.

Направление вектора _абс определяется его углами с осями координат:

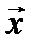( абс ^{^}, ) = аrс cos 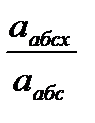= абс cos 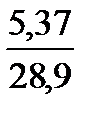= 79,3

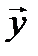( абс ^{^}, ) = аrс cos 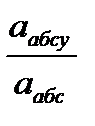= абс cos = 162,7

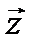( абс ^{^}, ) = аrс cos 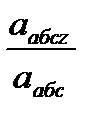= абс cos = 76,8

Задача 2.3

Задача 2.3 относится к плоскому движению твердого тела. Скорость ползуна для данного положения механизма можно вычислить с помощью как теоремы о проекциях скоростей двух точек тела, так и мгновенного центра скоростей шатуна. Для этого необходимо знать скорость какой-нибудь точки шатуна (например точки А) и направление скорости ползуна.

Ускорение ползуна в данный момент времени можно найти с помощью векторной формулы распределения ускорений точек плоской фигуры, спроектировав ее на два взаимно перпендикулярных направления. В качестве полюса удобно выбрать точку А. Исходные данные к задаче даны в табл. 2.4. и на рис.2.7.

Условие:

Кривошип ОА длиной R вращается вокруг неподвижной оси О с постоянной угловой скоростью w и приводит в движение шатун АВ длиной L и ползун В. Для заданного положения механизма найти скорость и ускорение ползуна В.

Примечание. Если при заданных значениях углов окажется, что шатун АВ перпендикулярен направляющим ползуна (см. рис. 2.7, схемы 1, 6), то значение угла b следует принять равным 15°.

Таблица 2.4

Цифра шифра	1-я цифра шифра	2-я цифра шифра	3-я цифра шифра
R, см	L, cм	a, град	b, град	w, c^-1	Номер схемы (рис. 2.7)

Рис. 2.7. Схемы к задаче 2.3.

Дата добавления: 2014-11-25