Пример решения задачи 2.3

Условие. Кривошип ОА длиной R=64 см вращается вокруг неподвижной оси О с постоянной угловой скоростью w=1 рад/с и приводит в движение шатун АВ длиной L=72 см и ползун В. Для положения механизма, заданного значениями углов a=45°, b=30,° найти скорость и ускорение ползуна В. Схема механизма приведена на рис. 2.8.

Рис. 2.8

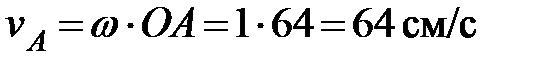Решение. 1. Определим скорость точки А как вращательную вокруг неподвижной точки О по соотношению . Для определения скорости точки В найдем положение мгновенного центра скоростейР, для чего покажем направление скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их скоростям v_A и v_B. Точка пересечения перпендикуляров будет являться мгновенным центром скоростей Р (см. рис. 2.8).

Рассмотрим движение шатуна в данный момент времени как вращательное относительно оси, проходящей через мгновенный центр скоростей Р перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна в этом случае

определяется из соотношения 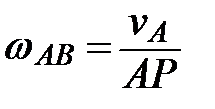, а скорость ползуна В как вращательная – из соотношения .

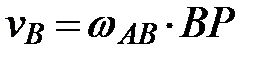Расстояния АР и BP определим из решения треугольника АВР, применив теорему синусов. Для заданного положения механизма получим

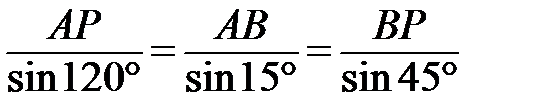, откуда

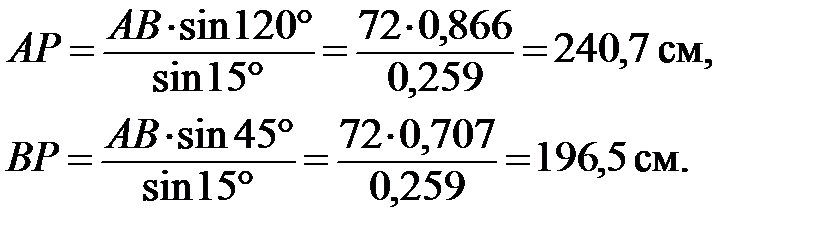
Подставив найденные значения расстояний в соответствующие формулы, получим 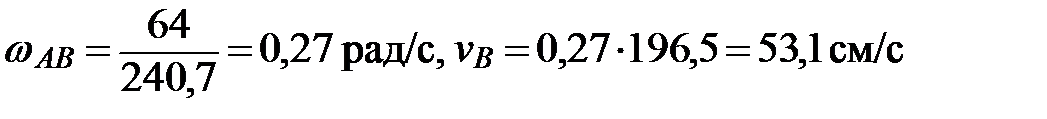. Направления скоростей показаны на рис. 2.8.

2. Для определения ускорения ползуна B воспользуемся векторным равенством:

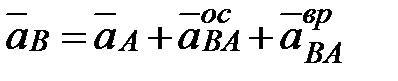, (1)

где 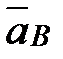– ускорение ползуна В;

– ускорение точки А, выбранной за полюс;

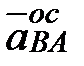– осестремительное (нормальное) ускорение точки В при ее вращении вокруг полюса А;

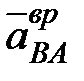– вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.

Ускорение точки А кривошипа при равномерном вращении вокруг неподвижной оси О состоит только из осестремительной составляющей, модуль которой определяется формулой 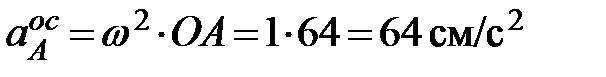. Вектор ускорения точки А направлен к оси вращения (рис.2.9), .

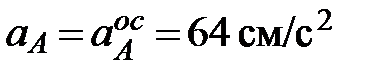Осестремительное ускорение точки В при ее вращении вокруг полюса А:

.

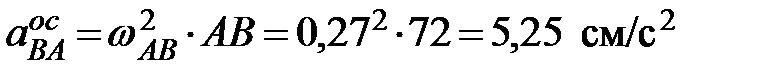Рис. 2.9.

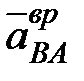Рассчитать вращательное ускорение обычным способом не представляется возможным, так как величина углового ускорения звена АВ неизвестна. Несмотря на это обстоятельство, векторное равенство (1) позволяет найти ускорение ползуна В. Для этого воспользуемся тем, что нам известно направления вектора 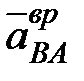(он перпендикулярен ускорению 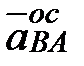) и вектора ускорения искомого ускорения 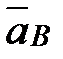(вдоль прямолинейной траектории точки В).

Проведем вектор ускорения 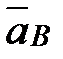точки В, предполагая, что он направлен противоположно скорости точки В. Спроектируем векторное равенство (1) на ось u, перпендикулярную ускорению 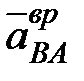и проходящую через точки А и В, получим 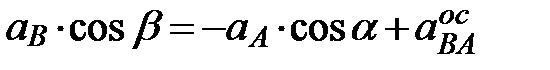. Отсюда

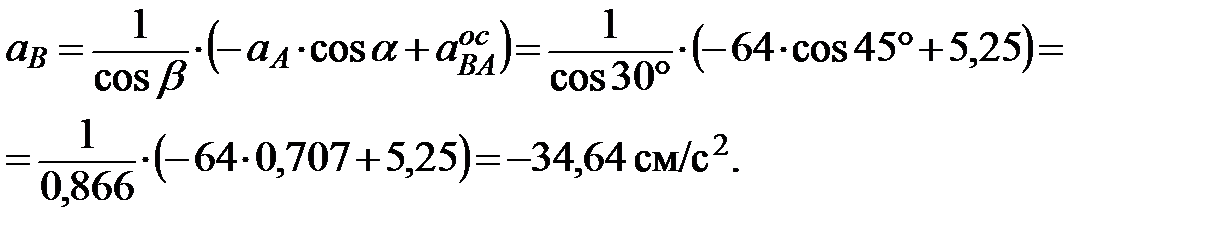
Знак минус показывает, что истинное направление ускорения точки В противоположно принятому.

3. КОНТРОЛЬНАЯ РАБОТА ПО РАЗДЕЛУ «ДИНАМИКА»

Задача 3.1

Задание относится к прямой задаче динамики точки: по известным (заданным) силам и начальным условиям движения требуется определить движение точки, получив уравнения движения. Для этого следует изобразить движущееся тело (точку) в произвольный момент времени, показать все действующие на тело (заданные) силы, освободиться от связей, заменив их действие соответствую-щими реакциями. Затем составить дифференциальные уравнения движения (два при криволинейном и одно при прямолинейном движениях) и проинтегрировать их. Значения постоянных интегрирования определить из начальных условий. Исходные данные для различных вариантов даны в табл. 3.1., а схемы приведены на рис. 3.1.

Таблица 3.1

Цифра шифра	1-я цифра шифра	2-я цифра шифра	3-я цифра шифра
v0, м/с	a, м	b, м	a, град	Силы, Н	Номер условия	Номер схемы (рис. 4.1)	f
F	P
		4,5	1,0				3.1.1		–
		5,0	1,5				3.1.1		–
		5,5	2,0				3.1.1		–
		6,0	2,5				3.1.1		–
		6,5	3,0				3.1.2		–
		7,0	3,5				3.1.2		–
		7,5	4,0				3.1.3		0,10
		8,0	4,5				3.1.3		0,12
		8,5	5,0				3.1.4		0,14
		9,0	5,5				3.1.4		0,16

Дата добавления: 2014-11-25